1.2 As A Percent
renascent
Sep 19, 2025 · 5 min read
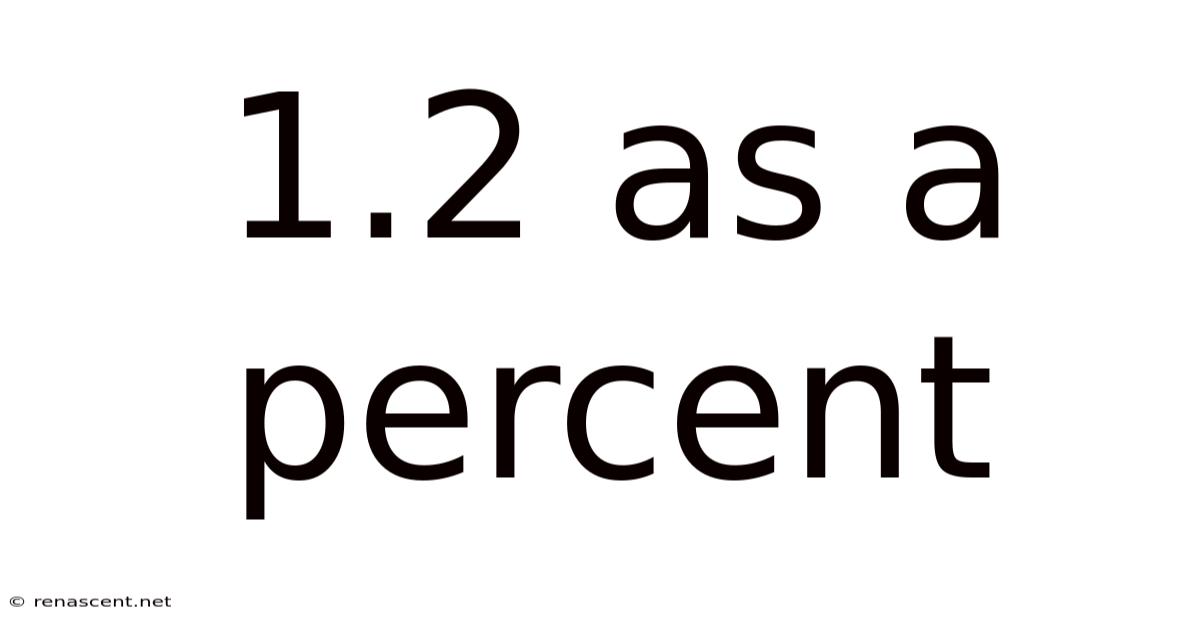
Table of Contents
Understanding 1.2 as a Percentage: A Comprehensive Guide
Introduction: Many everyday situations require us to understand and convert decimal numbers into percentages. Whether you're calculating discounts, interest rates, or tax percentages, knowing how to represent a decimal like 1.2 as a percentage is a crucial skill. This comprehensive guide will not only show you how to convert 1.2 to a percentage but also explore the underlying concepts, providing a thorough understanding of percentages and their applications. We'll delve into the mathematical principles, practical examples, and frequently asked questions, ensuring you confidently handle similar conversions in the future. This guide aims to empower you with the knowledge to manipulate percentages effectively in various contexts.
From Decimal to Percentage: The Conversion Process
The conversion of a decimal number to a percentage involves a simple yet fundamental mathematical operation: multiplication by 100. The percentage represents a fraction of 100. Therefore, to express 1.2 as a percentage, we follow these steps:
-
Multiply the decimal by 100: 1.2 * 100 = 120
-
Add the percentage symbol: 120%
Therefore, 1.2 as a percentage is 120%.
Why is 1.2 more than 100%? Understanding Percentage Values Greater Than 100%
The result of 120% might seem counterintuitive at first. We're used to percentages ranging from 0% to 100%, representing a portion of a whole. However, percentages greater than 100% simply indicate a value exceeding the original whole. Imagine you have a target of 100 units to produce. If you produce 120 units, you've exceeded your target by 20 units, which is represented as 120% of the target. In other words, you achieved 120% of your goal.
Real-World Applications of Percentages Greater Than 100%
Percentages exceeding 100% are commonplace in many real-world scenarios:
-
Business Growth: A company's revenue might increase by 150% compared to the previous year. This signifies a significant growth exceeding the initial revenue.
-
Stock Market: Stock prices can increase significantly, resulting in percentage increases exceeding 100%.
-
Inflation: Inflation rates exceeding 100% represent hyperinflation, a period of extremely rapid price increases.
-
Population Growth: A town's population might increase by 120% over a certain period, indicating substantial growth exceeding the initial population.
-
Project Completion: A project might be completed at 110% of its expected output, showing surpassing initial expectations.
These examples highlight that percentages beyond 100% are not an anomaly but rather a practical representation of values exceeding the reference point or original quantity.
Understanding the Mathematical Basis: Ratios and Fractions
At its core, a percentage is a ratio expressed as a fraction of 100. The decimal 1.2 can be expressed as the fraction 12/10. To convert this fraction to a percentage, we need to find an equivalent fraction with a denominator of 100:
(12/10) * (10/10) = 120/100
This fraction, 120/100, directly translates to 120%, confirming our earlier calculation. This approach underscores the fundamental connection between decimals, fractions, and percentages.
Practical Examples: Applying the 120% Conversion
Let's explore some practical scenarios to solidify our understanding of 1.2 as 120%:
Example 1: Increased Production
A factory aimed to produce 500 units of a product. Due to increased efficiency, they produced 600 units. To calculate the percentage increase, we perform the following calculation:
(600 - 500) / 500 * 100 = 20% increase
This means they exceeded their target by 20%, resulting in a total production of 120% (100% + 20%) of their initial goal.
Example 2: Investment Return
An investment of $1000 yielded a return of $1200. The percentage return is calculated as:
($1200 - $1000) / $1000 * 100 = 20% return on investment
Again, this translates to a 120% return relative to the initial investment.
Frequently Asked Questions (FAQ)
Q1: Can a percentage be greater than 100%?
Yes, absolutely. Percentages greater than 100% indicate a value exceeding the original amount or reference point.
Q2: How do I convert a percentage back to a decimal?
To convert a percentage back to a decimal, divide the percentage by 100. For example, 120% divided by 100 equals 1.2.
Q3: What if I have a decimal smaller than 1, such as 0.5? How do I convert it to a percentage?
The same principle applies. Multiply the decimal by 100 to get the percentage. 0.5 * 100 = 50%, representing half of the whole.
Q4: Are there any common mistakes to avoid when working with percentages?
One common mistake is incorrectly calculating percentage increases or decreases. Always ensure you're using the correct base value for your calculations. Another mistake is misinterpreting percentages greater than 100%. Remember they signify values exceeding the initial amount.
Advanced Concepts: Percentage Change and Growth Rates
Understanding percentage change is crucial in various applications, including finance and economics. Percentage change is calculated as:
(New Value - Old Value) / Old Value * 100
This formula allows us to determine the percentage increase or decrease between two values. When dealing with continuous growth, we might encounter exponential growth models where the percentage change itself changes over time. This leads to concepts like compound interest and exponential growth rates.
Conclusion: Mastering Percentage Conversions and Applications
Converting 1.2 to a percentage (120%) is a fundamental skill with wide-ranging applications. This guide has explored the mathematical basis, provided practical examples, and addressed frequently asked questions, ensuring a comprehensive understanding. Remember, percentages are powerful tools for representing proportions and changes. By mastering the principles discussed here, you will be well-equipped to handle percentages confidently in various contexts, from everyday calculations to more complex financial or scientific applications. The ability to seamlessly convert between decimals and percentages is a valuable asset in numerous fields. The key takeaway is to understand that percentages greater than 100% are perfectly valid and often represent significant increases or growth beyond the initial value.
Latest Posts
Latest Posts
-
Recurring Decimals To Fractions
Sep 19, 2025
-
Cat And Moon Tattoo
Sep 19, 2025
-
Gamma Eminence In Shadow
Sep 19, 2025
-
Changing A Flat Tyre
Sep 19, 2025
-
Female Crocodile One Piece
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1.2 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.