1 21 X 100
renascent
Sep 19, 2025 · 5 min read
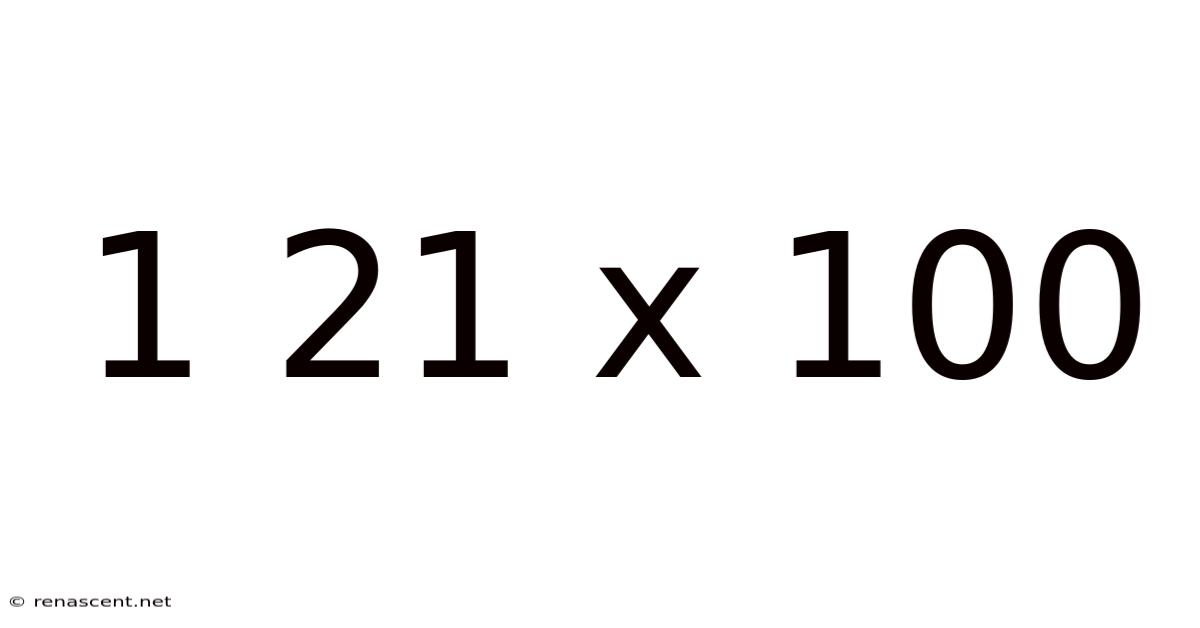
Table of Contents
Decoding 121 x 100: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 121 x 100, delving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and broader implications within various fields. We'll examine different methods for solving this problem, discuss the significance of the numbers involved, and explore how this seemingly basic calculation forms the foundation for more complex mathematical concepts. This comprehensive guide is perfect for students seeking a deeper understanding of multiplication, as well as anyone interested in the fascinating world of numbers and their real-world applications.
Understanding the Fundamentals: Multiplication Basics
At its core, multiplication is repeated addition. When we say 121 x 100, we are essentially adding 121 to itself 100 times. While this method is conceptually straightforward, it's impractical for larger numbers. Therefore, understanding efficient multiplication techniques is crucial. The problem 121 x 100 exemplifies several key principles:
-
Place Value: The position of each digit in a number determines its value (ones, tens, hundreds, etc.). Understanding place value is essential for correctly performing multiplication, especially with larger numbers. In 121, the '1' in the hundreds place represents 100, the '2' in the tens place represents 20, and the final '1' represents 1.
-
Distributive Property: This property allows us to break down complex multiplication problems into simpler ones. We can rewrite 121 x 100 as (100 + 20 + 1) x 100, and then distribute the 100 to each term: (100 x 100) + (20 x 100) + (1 x 100). This approach simplifies the calculation.
-
Multiplying by Powers of 10: Multiplying a number by 10, 100, 1000, and so on, involves simply adding zeros to the end of the number. This is because each power of 10 represents a shift in place value. Multiplying 121 by 100 means shifting the digits two places to the left, resulting in 12100.
Methods for Solving 121 x 100
Let's explore several methods to solve 121 x 100:
-
Direct Multiplication: This is the most straightforward method, especially for smaller numbers. You can use traditional long multiplication to obtain the answer:
121 x 100 ------ 000 0000 12100 ------ 12100 -
Using the Distributive Property: As explained above, we can break down 121 into its place values and then distribute the 100:
(100 x 100) + (20 x 100) + (1 x 100) = 10000 + 2000 + 100 = 12100
-
Multiplying by Powers of 10: This is the most efficient method for multiplying by 100. Simply add two zeros to the end of 121, giving us 12100.
The Significance of the Numbers: 121 and 100
The numbers 121 and 100 hold individual mathematical significance:
-
121: This is a perfect square (11 x 11 = 121). Perfect squares are numbers that can be obtained by squaring an integer. This property connects our multiplication problem to the concept of square roots and quadratic equations.
-
100: This is a perfect square (10 x 10 = 100) and a power of 10 (10²). Its significance stems from its use as a base unit in the metric system and its frequent appearance in percentage calculations. Multiplying by 100 is equivalent to finding 100% of a value.
Applications of 121 x 100 in Real-World Scenarios
While seemingly simple, the principles behind 121 x 100 have practical applications across various fields:
-
Finance: Calculating percentages, interest, or discounts often involves multiplying by powers of 10. For example, calculating 121% of a value requires multiplying that value by 1.21, which is related to our problem.
-
Engineering and Physics: Many engineering and physics calculations involve manipulating numbers and performing multiplications, often with larger numbers that can be broken down using similar methods.
-
Computer Science: Binary operations and bit manipulation rely on fundamental arithmetic, where the concept of place value and multiplication play a pivotal role.
-
Everyday Life: From calculating the total cost of 100 items costing $1.21 each to determining the area of a square with sides of 11 units (11 x 11 = 121 square units), this multiplication principle is surprisingly ubiquitous.
Expanding the Scope: Beyond 121 x 100
The problem 121 x 100 serves as a stepping stone to understanding more complex mathematical concepts:
-
Algebra: Replacing the numbers with variables (e.g., x x 100) introduces algebraic expressions and allows for solving equations.
-
Calculus: Derivatives and integrals involve the manipulation of functions, which are built upon basic arithmetic operations like multiplication.
-
Statistics: Statistical analysis relies heavily on calculations involving large datasets, often requiring efficient multiplication techniques.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to solve 121 x 100? A: The quickest way is to add two zeros to the end of 121, resulting in 12100.
-
Q: Why is understanding place value important in multiplication? A: Place value determines the value of each digit in a number, which is crucial for correctly aligning digits during multiplication and obtaining the accurate answer.
-
Q: Can I use a calculator to solve this problem? A: Yes, a calculator can provide the answer quickly. However, understanding the underlying mathematical principles is more valuable than simply obtaining the answer.
-
Q: Are there other methods to solve this type of problem? A: Yes, various methods exist, including using the distributive property, lattice multiplication, or even mental math techniques depending on the complexity of the numbers involved.
Conclusion: The Power of Simple Multiplication
The seemingly simple problem 121 x 100 provides a gateway to understanding fundamental mathematical concepts and their vast applications. By exploring different solution methods, analyzing the significance of the numbers involved, and considering real-world applications, we've gone beyond a simple arithmetic problem to appreciate the power and versatility of multiplication. This foundational skill forms the bedrock for more advanced mathematical concepts and plays a crucial role in various scientific, engineering, and everyday contexts. Remember, mastering the basics is key to unlocking the complexities of mathematics. Continue exploring, questioning, and applying your knowledge to discover the fascinating world of numbers!
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 21 X 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.