1 3 Of 120
renascent
Sep 17, 2025 · 5 min read
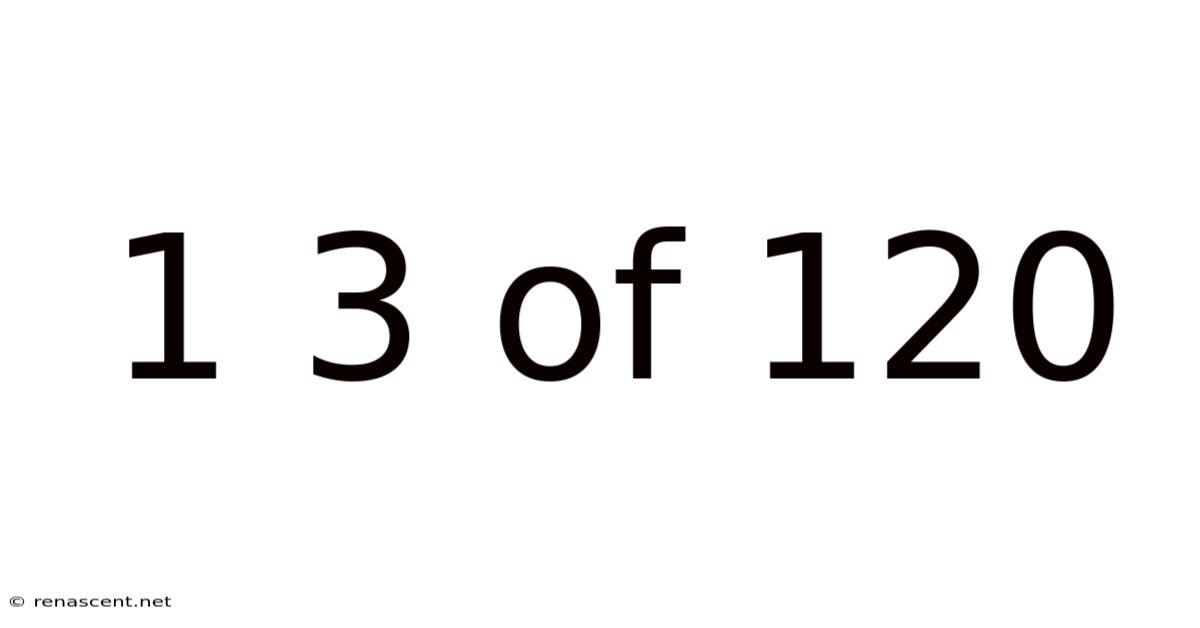
Table of Contents
Decoding 1/3 of 120: A Comprehensive Guide to Fractions and Percentages
Understanding fractions and percentages is fundamental to various aspects of life, from everyday calculations to complex scientific analyses. This article will delve into the seemingly simple problem of finding 1/3 of 120, breaking down the process step-by-step and exploring the underlying mathematical concepts. We'll cover multiple approaches to solving this problem, explain the logic behind each method, and provide you with the tools to confidently tackle similar problems in the future. This comprehensive guide is suitable for students, professionals, or anyone seeking a deeper understanding of fractions and percentages.
Understanding the Problem: 1/3 of 120
The phrase "1/3 of 120" essentially asks: what is one-third of the number 120? This involves understanding the concept of fractions and how they relate to whole numbers. The fraction 1/3 represents one part out of three equal parts of a whole. In this case, the whole is 120. Therefore, we need to divide 120 into three equal parts and then determine the value of one of those parts.
Method 1: Direct Division
The most straightforward method is to directly divide 120 by 3. This is because "of" in mathematical terms usually implies multiplication, but in this context of finding a fraction of a number, it translates to division. The equation becomes:
120 ÷ 3 = 40
Therefore, 1/3 of 120 is 40.
This method is intuitive and easily applicable to similar problems. To find x/y of z, simply divide z by y. The result is x parts of z.
Method 2: Fraction Multiplication
Alternatively, we can express the problem as a multiplication problem involving fractions. Remember that "of" can be interpreted as multiplication. So, we can write the problem as:
(1/3) × 120
To multiply a fraction by a whole number, we can convert the whole number into a fraction by placing it over 1:
(1/3) × (120/1)
Now, multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 120) / (3 × 1) = 120/3
Finally, simplify the fraction by dividing the numerator by the denominator:
120/3 = 40
This method reinforces the understanding of fraction multiplication and provides a more formal approach to solving the problem. It's particularly useful when dealing with more complex fractions.
Method 3: Percentage Conversion
While not the most efficient method for this specific problem, converting the fraction to a percentage offers a valuable understanding of the relationship between fractions and percentages.
First, convert the fraction 1/3 into a percentage. To do this, divide the numerator by the denominator and multiply by 100:
(1 ÷ 3) × 100 ≈ 33.33%
Now, find 33.33% of 120:
(33.33/100) × 120 ≈ 40
This approach highlights the interchangeability of fractions and percentages and provides another perspective on the problem. It’s particularly useful when dealing with real-world problems where percentages are commonly used.
Extending the Concept: Applications and Variations
The core concepts explored here – fractions, percentages, and division – are widely applicable in various scenarios. Let’s explore some variations and applications:
-
Finding other fractions of 120: The same methods can be used to calculate any fraction of 120. For example, to find 2/3 of 120, you would multiply 120 by 2/3, which results in 80. Similarly, finding 1/4 of 120 would involve dividing 120 by 4, resulting in 30.
-
Finding a percentage of a different number: The principle extends to finding any percentage of any number. For instance, finding 25% of 80 involves converting 25% to a fraction (1/4) and then multiplying it by 80, resulting in 20.
-
Real-world applications: This calculation is vital in various real-world situations, including:
- Calculating discounts: A 33.33% discount on a $120 item would result in a $40 discount.
- Portioning ingredients: Dividing ingredients in recipes often involves fractions and percentages.
- Data analysis: Understanding fractions and percentages is crucial for interpreting statistical data.
- Financial calculations: Interest calculations and profit margins frequently utilize fractions and percentages.
Illustrative Examples: Stepping Beyond the Basics
Let's solidify our understanding with a few more complex examples:
Example 1: A farmer harvests 180 apples. He plans to use 2/5 of the apples to make apple pie and 1/3 of the remaining apples for apple sauce. How many apples will he use for apple sauce?
First, calculate the number of apples used for apple pie: (2/5) * 180 = 72 apples.
Next, find the number of apples remaining: 180 - 72 = 108 apples.
Finally, calculate the number of apples used for apple sauce: (1/3) * 108 = 36 apples.
Example 2: A shop owner offers a 15% discount on a $250 item. What is the discounted price?
First, calculate the discount amount: (15/100) * $250 = $37.50.
Then, subtract the discount from the original price: $250 - $37.50 = $212.50. The discounted price is $212.50.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate a fraction of a number?
A: The easiest way is usually direct division. Divide the number by the denominator of the fraction, then multiply the result by the numerator.
Q: Can I use a calculator for these calculations?
A: Absolutely! Calculators are helpful, especially for more complex fractions or percentages.
Q: Why is understanding fractions and percentages important?
A: Fractions and percentages are essential for everyday life, from cooking and shopping to finance and data analysis. They help us understand proportions and relationships between quantities.
Q: What if the fraction doesn't divide evenly?
A: If the fraction doesn't divide evenly, you'll get a decimal or a fraction as the result. For example, 1/7 of 120 is approximately 17.14.
Q: Are there any online tools to help with these calculations?
A: Yes, many online calculators and websites are available to assist with fraction and percentage calculations. However, understanding the underlying principles is crucial for problem-solving beyond simple calculations.
Conclusion: Mastering Fractions and Percentages
This article has comprehensively explored the calculation of 1/3 of 120, demonstrating multiple approaches and highlighting the broader applications of fractions and percentages. Understanding these fundamental mathematical concepts is not only essential for academic success but also empowers you to confidently navigate numerous real-world scenarios. By mastering these skills, you'll develop a deeper appreciation for mathematical principles and their practical significance in everyday life. Remember to practice regularly, and don't hesitate to explore further resources to solidify your understanding. With consistent practice and a curious mindset, you'll quickly become proficient in working with fractions and percentages.
Latest Posts
Latest Posts
-
1 5 Kg To Lbs
Sep 17, 2025
-
33 Lbs In Kg
Sep 17, 2025
-
113 4 Kg In Stone
Sep 17, 2025
-
800 Hours In Days
Sep 17, 2025
-
Dali Elephants And Swans
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.