1 4 Times 5
renascent
Sep 22, 2025 · 7 min read
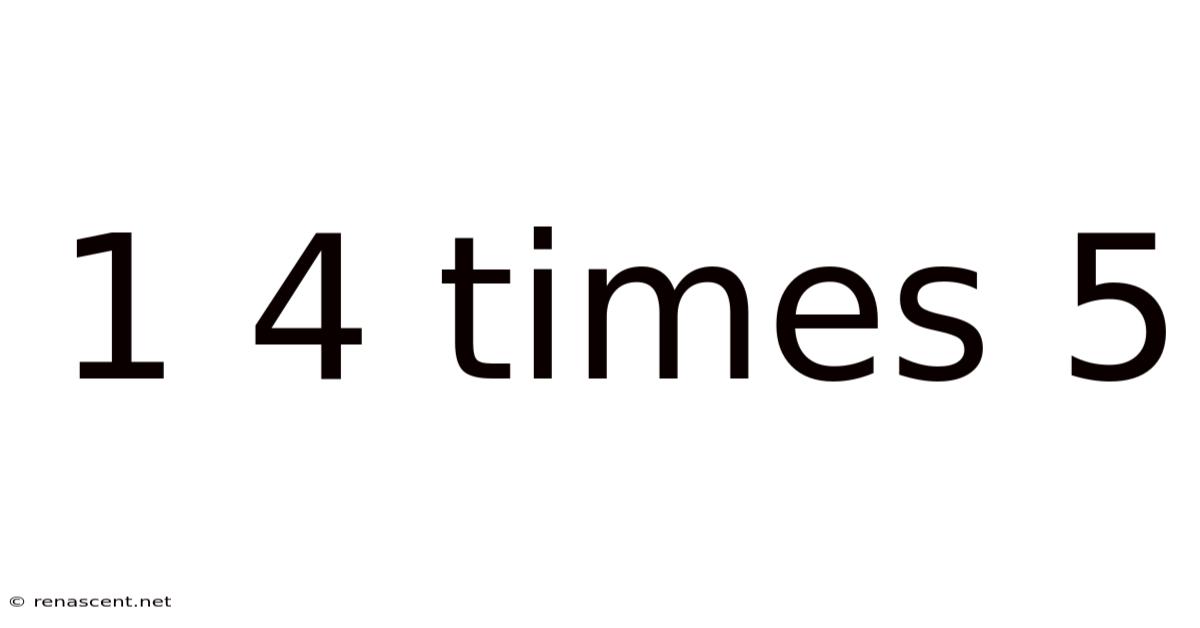
Table of Contents
Unraveling the Mystery: A Deep Dive into 1 x 4 x 5
This article explores the seemingly simple mathematical expression "1 x 4 x 5," delving far beyond the immediate answer to uncover the underlying principles, related concepts, and broader applications within mathematics and beyond. We'll uncover the beauty of this seemingly basic calculation and explore how it relates to more complex mathematical ideas. This exploration is ideal for anyone looking to strengthen their fundamental understanding of arithmetic, algebra, and even the philosophy of mathematics.
Introduction: Beyond the Obvious Answer
At first glance, 1 x 4 x 5 appears trivial. The answer, 20, is quickly calculated. However, this seemingly simple equation provides a fertile ground for exploring fundamental mathematical concepts. This article will dissect this expression, exploring its components, its place within the broader mathematical landscape, and its implications for problem-solving and critical thinking. We'll look at it from the perspective of arithmetic, algebra, and even touch upon its relevance to more advanced mathematical fields.
1. Understanding Multiplication: The Foundation
Multiplication, at its core, is repeated addition. 1 x 4 x 5 can be interpreted as:
- 1 x 4: This is adding the number 1 four times (1 + 1 + 1 + 1 = 4).
- (1 x 4) x 5: This takes the result of 1 x 4 (which is 4) and adds it five times (4 + 4 + 4 + 4 + 4 = 20).
This fundamental understanding is crucial for grasping more complex mathematical operations. It's the building block upon which more advanced concepts, like algebra and calculus, are built. The commutative, associative, and distributive properties of multiplication are essential to solving more intricate equations.
2. The Commutative Property: Rearranging the Numbers
The commutative property of multiplication states that the order of the numbers does not affect the result. This means 1 x 4 x 5 is equivalent to 4 x 1 x 5, 5 x 4 x 1, and any other permutation of these numbers. This seemingly simple concept is powerful because it allows us to rearrange numbers to make calculations easier. For example, multiplying by 1 is always the number itself, so we could rearrange this equation to make the calculation more straightforward: 1 x 4 x 5 = 1 x (4 x 5) = 1 x 20 = 20
3. The Associative Property: Grouping the Numbers
The associative property of multiplication dictates that the grouping of numbers does not affect the outcome. This means (1 x 4) x 5 is the same as 1 x (4 x 5). This property allows for flexibility in how we approach complex calculations. We can strategically group numbers to simplify the process. In this specific case, the associative property makes the calculation easier as 4 x 5 is 20, and then multiplying by 1, which is an identity operation, gives us 20 directly.
4. Applying the Distributive Property: Expanding the Possibilities
While not directly applicable to this simple example in its pure form, the distributive property shows how multiplication interacts with addition and subtraction. If we were to expand this expression to include addition or subtraction, the distributive property would become relevant. For example, if we had 1 x (4 + 1) x 5, we would distribute the 1 and the 5 to both terms within the parentheses (1 x 4 x 5) + (1 x 1 x 5) = 20 + 5 = 25
5. Algebraic Representation: Beyond Numbers
The expression 1 x 4 x 5 can be represented algebraically. Let's assign variables:
- Let a = 1
- Let b = 4
- Let c = 5
Our expression becomes a x b x c = 20. This seemingly small step opens the door to more complex algebraic manipulations and the solving of equations involving unknowns. We can use this basic equation as a simple example to introduce algebraic concepts to beginners.
6. Geometric Interpretation: Visualizing Multiplication
Visualizing multiplication can greatly enhance understanding. We can represent 1 x 4 x 5 geometrically:
- 1: Represents a single unit.
- 4: Represents four units laid out in a row or column.
- 5: Represents five rows or columns of those four units.
This creates a rectangular prism with dimensions 1 x 4 x 5, with a total volume of 20 cubic units. This visual representation connects abstract mathematical concepts to tangible, real-world objects.
7. Applications in Real-World Scenarios:
The simple calculation 1 x 4 x 5 has numerous real-world applications. Imagine:
- Buying items: You buy 1 pack of apples with 4 apples per pack, and you buy 5 packs. You end up with 20 apples.
- Arranging objects: You arrange objects in a 1 x 4 x 5 grid or rectangular prism. You would have 20 objects in total.
- Calculating area: A rectangle has a width of 4 and a length of 5, then its area could be calculated as (1 unit depth) x 4 x 5= 20 square units.
- Simple Programming: In basic computer programming, this could represent simple array manipulation or calculations of various types. The simplicity of this equation makes it ideal for illustrating fundamental coding concepts.
These examples demonstrate the practical relevance of seemingly simple mathematical expressions. These applications often go unnoticed, but are prevalent in everyday life.
8. Expanding the Concept: Introduction to Factorials and Combinations
While not directly involved in this specific calculation, expanding upon the concept can lead us to related mathematical topics. For example, understanding the numbers 1, 4, and 5 as individual factors can help in comprehending factorials (e.g., 5! = 5 x 4 x 3 x 2 x 1) and combinations, which are fundamental concepts in probability and statistics. These advanced concepts build upon the basic understanding of multiplication.
9. Number Theory Connections: Divisibility and Prime Factorization
The number 20, the result of 1 x 4 x 5, offers insights into number theory. We can analyze its divisors (1, 2, 4, 5, 10, 20), and its prime factorization (2² x 5). This prime factorization is unique to 20 and is crucial in various number theory applications. The concept of prime numbers, which are only divisible by 1 and themselves, is fundamentally important in many mathematical areas. Understanding the prime factorization of 20 helps in grasping more advanced mathematical concepts like modular arithmetic.
10. Beyond Arithmetic: A Glimpse into Higher Mathematics
While this expression is primarily an arithmetic exercise, it lays the groundwork for understanding more advanced mathematical concepts. The principles of multiplication, commutativity, associativity, and the distributive property all extend into algebra, calculus, and even abstract algebra. The simple act of multiplying 1, 4, and 5 is a foundational step in a much larger mathematical landscape.
Frequently Asked Questions (FAQ)
-
Q: Is there only one way to calculate 1 x 4 x 5?
- A: No. Due to the commutative and associative properties, there are multiple ways to arrange and group the numbers to arrive at the same result (20).
-
Q: What if one of the numbers was zero?
- A: If any of the numbers were zero, the entire product would be zero. This is because any number multiplied by zero equals zero.
-
Q: What if the numbers were negative?
- A: If any of the numbers were negative, the result would depend on the number of negative numbers. An odd number of negative numbers would result in a negative product, while an even number of negative numbers would result in a positive product.
-
Q: Can this be applied to more than three numbers?
- A: Absolutely. The principles of multiplication, commutativity, and associativity extend to any number of factors.
-
Q: Is there a practical application beyond simple arithmetic?
- A: Yes, the underlying principles are used extensively in various fields, including physics, engineering, computer science, and finance. Complex calculations rely heavily on the basic mathematical operations we've explored.
Conclusion: The Significance of Simplicity
The seemingly simple expression 1 x 4 x 5 offers a gateway to a vast world of mathematical concepts. By dissecting this equation, we've uncovered fundamental principles that underpin more advanced mathematical operations. Its simplicity belies its significance, showcasing the power of understanding basic principles to solve complex problems. The exploration of this simple equation reveals the beauty and interconnectedness of mathematics, illustrating how even the most basic concepts form the foundation for more intricate and powerful ideas. Remember, the journey to mastering mathematics begins with a strong grasp of fundamentals, and this exploration provides a solid base for that journey.
Latest Posts
Latest Posts
-
South Americas Largest City
Sep 23, 2025
-
How To Spell Necessarily
Sep 23, 2025
-
270 Lb In Kg
Sep 23, 2025
-
Scientific Name For Sheep
Sep 23, 2025
-
Erosion By Water Pictures
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Times 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.