1 Divided By 2/3
renascent
Sep 17, 2025 · 5 min read
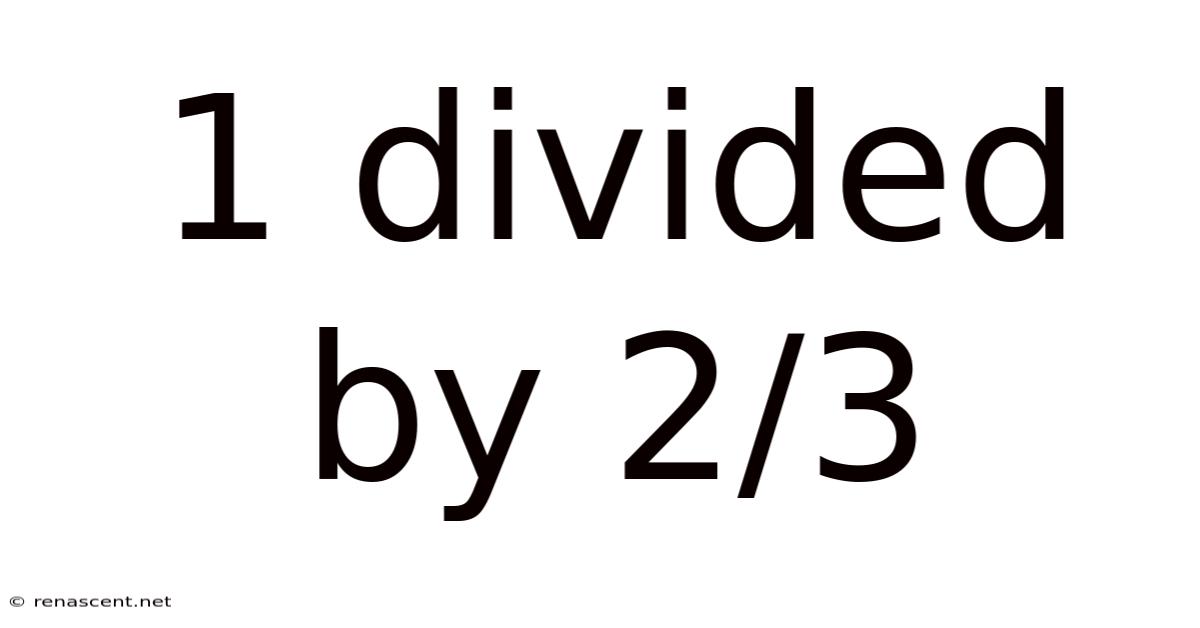
Table of Contents
Understanding 1 Divided by 2/3: A Deep Dive into Fraction Division
Many people find fractions challenging, and division involving fractions can seem especially daunting. This article will demystify the process of dividing 1 by 2/3, explaining the concept in a clear, step-by-step manner suitable for everyone, from elementary school students to adults brushing up on their math skills. We'll cover the fundamental principles, explore different methods for solving this problem, and delve into the underlying mathematical reasons behind the solution. By the end, you'll not only know the answer but also understand why it's the answer.
Understanding the Problem: 1 ÷ (2/3)
The problem, 1 ÷ (2/3), asks: "How many times does 2/3 go into 1?" This seemingly simple question highlights a crucial concept in fraction division: we're essentially looking for the number of times a smaller fraction (2/3) fits into a larger number (1). This is different from multiplying or adding fractions, and requires a specific approach.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is perhaps the most common and easiest method to understand for dividing fractions. It's based on the principle of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
Here's how to apply the "Keep, Change, Flip" method to solve 1 ÷ (2/3):
- Keep: Keep the first number (the dividend) as it is. In this case, it's 1.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – take its reciprocal. The reciprocal of 2/3 is 3/2.
This transforms the problem from 1 ÷ (2/3) into 1 × (3/2). Now we can easily multiply:
1 × (3/2) = 3/2
Therefore, 1 divided by 2/3 equals 3/2, or 1 ½. This means that 2/3 fits into 1 one and a half times.
Method 2: Visual Representation
Visualizing the problem can make it easier to grasp. Imagine a pizza cut into three slices. 2/3 of the pizza represents two of these slices. The question "1 ÷ (2/3)" asks: how many sets of two slices are there in one whole pizza?
You can see that there is one full set of two slices (2/3) and half a set left over. This visually demonstrates that 2/3 fits into 1 one and a half times, confirming our earlier answer of 3/2 or 1 ½.
Method 3: Understanding Division as Repeated Subtraction
Division can be conceptually understood as repeated subtraction. How many times can we subtract 2/3 from 1 before we reach 0?
Let's demonstrate this:
- Start with 1.
- Subtract 2/3: 1 - 2/3 = 1/3
- We can't subtract another 2/3 because 1/3 is less than 2/3. However, we subtracted 2/3 once. But we have 1/3 remaining. And 1/3 is exactly half of 2/3. Therefore, we subtracted 2/3 once and half of 2/3, which translates to 1 and 1/2 times.
Method 4: Converting to Improper Fractions and Cross-Multiplication
While the "Keep, Change, Flip" method is generally preferred for its simplicity, you can also solve this using improper fractions. Remember that any whole number can be expressed as a fraction with a denominator of 1. So, 1 can be written as 1/1.
Now our problem is (1/1) ÷ (2/3). In this method, we will cross multiply:
(1/1) ÷ (2/3) = (1 * 3) / (1 * 2) = 3/2
Again, this results in 3/2, or 1 ½. This method emphasizes the relationship between numerator and denominator during the division process.
The Mathematical Explanation: Reciprocals and Multiplication
The core reason why the "Keep, Change, Flip" method works lies in the relationship between division and multiplication. Division by a fraction is equivalent to multiplying by its reciprocal. This can be proven mathematically. Consider the general case:
a ÷ (b/c) = a × (c/b)
If we express this in terms of fractions, we can explain the method more formally using the multiplicative inverse:
a/1 ÷ b/c = a/1 * c/b = (ac) / (1b) = ac/b
This shows that dividing by a fraction is the same as multiplying by its reciprocal. The essence of this is that multiplying by the reciprocal "undoes" the division by the fraction.
Frequently Asked Questions (FAQ)
Q: Can I solve this problem using a calculator?
A: Yes, most calculators can handle fraction division. Enter the problem as 1 ÷ (2/3), ensuring you use the correct parentheses, and the calculator will provide the answer as 1.5 or 3/2, depending on its settings.
Q: What if the first number wasn't 1? How would I solve something like 5 ÷ (2/3)?
A: The "Keep, Change, Flip" method works exactly the same:
- Keep: 5
- Change: ÷ becomes ×
- Flip: 2/3 becomes 3/2
The problem becomes 5 × (3/2) = 15/2 = 7 ½
Q: Why is it important to understand fraction division?
A: Understanding fraction division is fundamental to various mathematical concepts and real-world applications. It is crucial in areas such as:
- Measurement: Converting units, calculating areas, and volumes often involves fraction division.
- Cooking and Baking: Following recipes accurately requires understanding how to divide fractions when scaling ingredients up or down.
- Construction and Engineering: Precise calculations in these fields are dependent on accurate fraction division.
- Finance: Calculating proportions, interest rates, and discounts frequently involve working with fractions and division.
Conclusion
Dividing 1 by 2/3 might initially appear complex, but by understanding the underlying principles and applying the appropriate methods – like the "Keep, Change, Flip" method – it becomes a straightforward calculation. The answer, 3/2 or 1 ½, is not just a numerical result; it represents a fundamental understanding of fraction division. This understanding extends far beyond simple calculations, forming the foundation for more advanced mathematical concepts and practical applications in various aspects of life. By mastering fraction division, you’re equipping yourself with a valuable tool for problem-solving in numerous fields. Remember to practice regularly; the more you work with fractions, the more comfortable and confident you will become.
Latest Posts
Latest Posts
-
5 6 Divided By 8
Sep 17, 2025
-
125 Miles To Km
Sep 17, 2025
-
1 4th Of 32
Sep 17, 2025
-
Frida Kahlo Monkey Portrait
Sep 17, 2025
-
98 1 F To C
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.