1 Divided By 3/5
renascent
Sep 25, 2025 · 6 min read
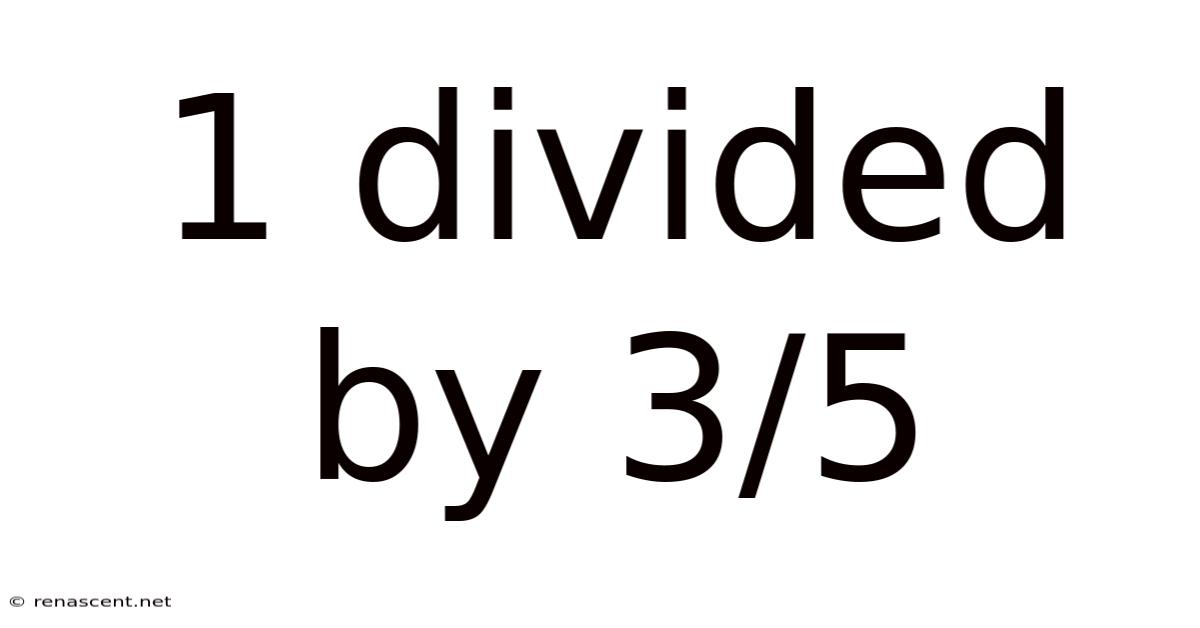
Table of Contents
Understanding 1 Divided by 3/5: A Comprehensive Guide
Dividing by fractions can seem daunting, but it's a fundamental concept in mathematics with real-world applications. This comprehensive guide will walk you through solving "1 divided by 3/5," explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common questions. Understanding this seemingly simple problem unlocks a deeper understanding of fraction manipulation and its practical uses.
Introduction: Why This Matters
The problem, "1 divided by 3/5," might appear straightforward, but it's a crucial stepping stone to understanding more complex fraction division problems. Mastering this concept builds a solid foundation for algebra, calculus, and various practical applications in fields like cooking, construction, and engineering. We will break down this problem methodically, ensuring you grasp not just the answer but also the why behind the solution. This understanding will empower you to tackle similar problems with confidence and accuracy.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is arguably the most common and easiest method to divide fractions. It's based on the principle of reciprocals. The reciprocal of a fraction is obtained by swapping its numerator and denominator.
Steps:
-
Keep: Keep the first number (the dividend) as it is. In this case, it's 1.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (or find the reciprocal of) the second number (the divisor). The reciprocal of 3/5 is 5/3.
Therefore, the problem transforms from 1 ÷ 3/5 to 1 × 5/3.
-
Multiply: Now, simply multiply the numerators together and the denominators together.
1 × 5 = 5 1 × 3 = 3
This gives us the answer: 5/3.
- Simplify (if necessary): In this case, the fraction 5/3 is already in its simplest form (meaning there is no common factor other than 1 for both numerator and denominator). However, if we wanted to express it as a mixed number, we would perform the division: 5 ÷ 3 = 1 with a remainder of 2. Therefore, 5/3 can also be expressed as 1 and 2/3 or 1 2/3.
Method 2: Understanding Division as Repeated Subtraction
While the "keep, change, flip" method is efficient, understanding the core concept of division helps solidify the knowledge. Division asks, "How many times does the divisor fit into the dividend?"
Let's visualize this with our problem: 1 divided by 3/5. We can think of this as asking, "How many times does 3/5 fit into 1?"
It's helpful to use a visual aid here. Imagine a whole unit (representing the number 1). Now, imagine dividing that unit into fifths. Each fifth is 1/5. The fraction 3/5 represents three of these fifths.
To figure out how many times 3/5 goes into 1, we can see that there's one whole unit and we're trying to figure out how many sets of 3/5 we can make from that whole unit. In essence, if we take 3/5 away once, that's 3/5 of the whole. What's left is 2/5. Therefore we didn't fit in another 3/5. However, this way of understanding doesn't provide the exact number.
We can get a closer approximation by seeing how many 3/5 is there in 1/5. If we try to fit 3/5 into 1, we will be able to take out 3/5 from 1 only once, but not completely, so this method is not appropriate here. That's why the "keep, change, flip" method is preferred as it gives the exact numerical solution rather than an estimation.
Method 3: Using the Definition of Division
Mathematically, division is defined as the inverse operation of multiplication. If a ÷ b = c, then a = b × c. Let's apply this to our problem:
1 ÷ (3/5) = x
This means: 1 = (3/5) × x
To solve for x, we need to isolate x. We can do this by multiplying both sides of the equation by the reciprocal of 3/5 (which is 5/3):
(5/3) × 1 = (5/3) × (3/5) × x
This simplifies to:
5/3 = x
Therefore, x = 5/3, confirming the results obtained using the "keep, change, flip" method. This method provides a deeper, more formal understanding of the process.
Explanation: Why the "Keep, Change, Flip" Works
The "keep, change, flip" method is a shortcut derived from the definition of division and the properties of fractions. When we divide by a fraction, we are essentially multiplying by its reciprocal. This is because dividing by a number is the same as multiplying by its multiplicative inverse (reciprocal).
Consider this: Dividing by 2 is the same as multiplying by 1/2. Dividing by 1/3 is the same as multiplying by 3.
Practical Applications
Understanding fraction division has many practical applications:
-
Cooking: Scaling recipes up or down requires dividing fractions. For example, if a recipe calls for 2/3 cup of flour and you want to make half the recipe, you need to calculate (2/3) ÷ 2.
-
Construction: Calculating material requirements often involves dividing fractions.
-
Sewing: Determining fabric quantities for a project might require fraction division.
-
Data Analysis: Dealing with proportions and ratios frequently involves fraction manipulation.
-
Financial calculations: many financial calculations involves fractions to measure proportions, ratios, etc.
Frequently Asked Questions (FAQs)
Q: Why can't I just divide the numerators and denominators directly when dividing fractions?
A: You can only directly divide numerators and denominators when multiplying fractions. Division involves finding how many times one fraction goes into another, which requires the "keep, change, flip" method or equivalent approaches.
Q: Can I use a calculator to solve this?
A: Yes, most calculators can handle fraction division. However, understanding the underlying method is crucial for problem-solving and avoids reliance on technology in all situations.
Q: What if the number I'm dividing by is a whole number? How does the "keep, change, flip" method apply?
A: A whole number can be expressed as a fraction with a denominator of 1. For example, 2 can be expressed as 2/1. You would then apply the "keep, change, flip" method as usual. For example, (3/4) ÷ 2 becomes (3/4) × (1/2) = 3/8.
Q: What if the first number isn't 1?
A: The process remains the same. For example, (2/3) ÷ (1/4) would become (2/3) × (4/1) = 8/3 = 2 2/3.
Conclusion: Mastering Fraction Division
The problem of 1 divided by 3/5, while seemingly simple, highlights the importance of understanding fraction division. Whether you use the "keep, change, flip" method or the more formal approach based on the definition of division, understanding the underlying principles empowers you to solve more complex fraction problems and confidently apply this crucial skill to various real-world scenarios. Remember, practice makes perfect! The more you work with fractions, the more comfortable and proficient you will become. Don't be afraid to revisit this explanation and try out different problems to solidify your understanding. This understanding is a significant step towards greater mathematical fluency.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 Divided By 3/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.