1 Quarter Of 16
renascent
Sep 24, 2025 · 5 min read
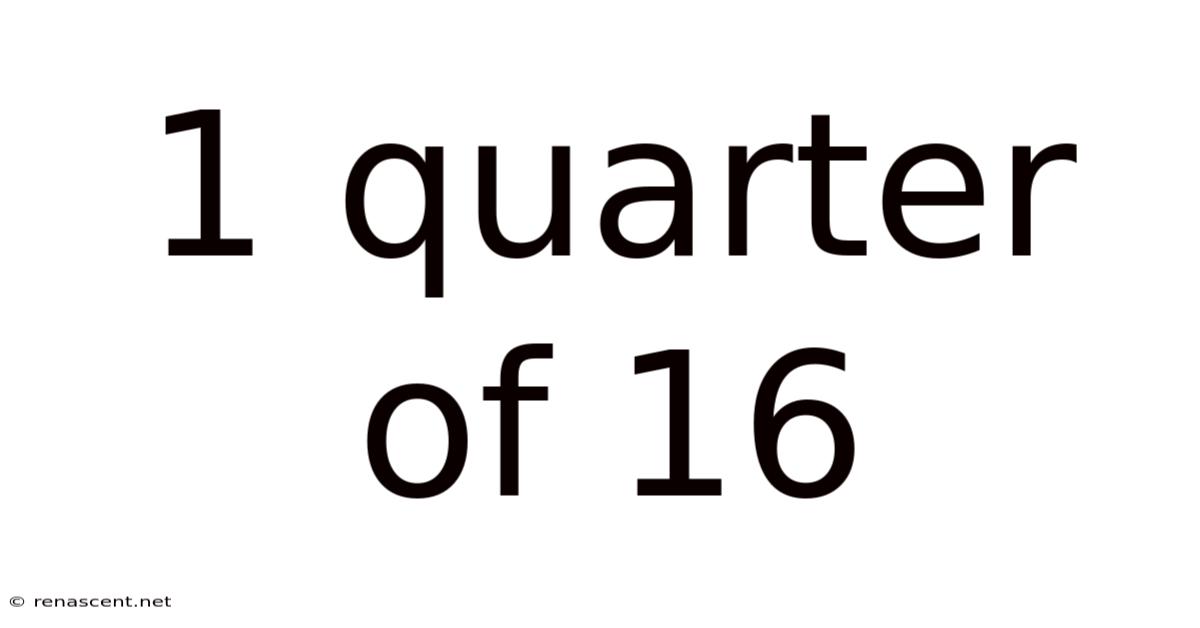
Table of Contents
Decoding the Mystery: Understanding One Quarter of Sixteen
What is one quarter of sixteen? This seemingly simple question, often encountered in elementary math, can serve as a gateway to understanding fundamental concepts in fractions, percentages, and even more advanced mathematical operations. This article will delve into the solution, exploring various methods for calculating it, explaining the underlying principles, and expanding on its applications in real-world scenarios. We'll also address common misconceptions and frequently asked questions to ensure a comprehensive understanding.
Understanding Fractions: The Building Blocks
Before diving into the calculation, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
In our case, "one quarter" translates to the fraction 1/4. The denominator, 4, tells us the whole is divided into four equal parts, and the numerator, 1, signifies we're interested in just one of those parts.
Calculating One Quarter of Sixteen: Three Approaches
There are several ways to calculate one quarter of sixteen:
1. Using Division:
The most straightforward approach is to divide 16 by 4. This directly reflects the meaning of "one quarter": finding one of four equal parts.
16 ÷ 4 = 4
Therefore, one quarter of sixteen is 4.
2. Using Fraction Multiplication:
We can express "one quarter of sixteen" as a multiplication problem: (1/4) * 16. To multiply a fraction by a whole number, we multiply the numerator by the whole number and keep the denominator the same:
(1/4) * 16 = (1 * 16) / 4 = 16 / 4 = 4
Again, the answer is 4.
3. Visual Representation:
Imagine a pizza cut into 16 slices. One quarter of the pizza would consist of 16 slices divided into four equal groups. Each group would contain 16/4 = 4 slices. This visual method helps solidify the concept and makes it more intuitive, particularly for younger learners.
Expanding the Concept: Percentages and Decimals
The concept of one quarter extends beyond simple fractions. It's directly related to percentages and decimals:
-
Percentage: One quarter is equivalent to 25%. This is because 1/4 represents one part out of four, and 25% represents 25 parts out of 100. Both fractions are equivalent: 1/4 = 25/100.
-
Decimal: One quarter is equivalent to 0.25 in decimal form. This is obtained by dividing the numerator (1) by the denominator (4): 1 ÷ 4 = 0.25.
Understanding these interrelationships helps build a stronger grasp of mathematical concepts and their interconnectedness.
Real-World Applications: Beyond the Classroom
The ability to calculate fractions like one quarter isn't confined to theoretical mathematical problems. It has countless practical applications in everyday life:
-
Sharing equally: Dividing resources, such as food, money, or tasks, among four people requires calculating one quarter for each individual.
-
Discounts and sales: A 25% discount on an item means calculating one quarter of the original price to determine the amount of the discount.
-
Recipe scaling: Halving or quartering a recipe involves using fractions to adjust the ingredient quantities accordingly.
-
Measurement: Understanding fractions is essential when working with various measurement systems, converting units, and performing calculations involving length, volume, or weight.
-
Financial calculations: Fractions and percentages are fundamental in financial calculations, including interest rates, tax calculations, and investment returns.
Addressing Common Misconceptions
-
Confusing numerator and denominator: A common mistake is reversing the numerator and denominator, leading to incorrect calculations. Remember, the denominator represents the total parts, and the numerator shows the parts we are considering.
-
Incorrect multiplication of fractions: When multiplying fractions, remember to multiply the numerators and the denominators separately. Don't add or subtract them.
-
Difficulty visualizing fractions: Using visual aids, like diagrams or real-world objects, can help in understanding and visualizing fractions more effectively.
Frequently Asked Questions (FAQ)
Q1: How do I calculate more than one quarter of a number?
A1: To calculate, for example, three quarters of 16, you multiply the fraction (3/4) by 16: (3/4) * 16 = (3 * 16) / 4 = 48/4 = 12.
Q2: What if the number isn't easily divisible by four?
A2: If the number isn't a multiple of four, the result will be a fraction or a decimal. For example, one quarter of 17 is 17/4 = 4.25.
Q3: How can I convert a fraction to a percentage?
A3: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100. For example, 1/4 = (1 ÷ 4) * 100 = 25%.
Q4: Why is understanding fractions important?
A4: Understanding fractions is crucial for various aspects of life, from everyday tasks to complex mathematical and scientific calculations. It's a foundational element of numeracy and problem-solving skills.
Conclusion: Mastering the Fundamentals
Calculating one quarter of sixteen, while seemingly simple, provides a valuable opportunity to reinforce fundamental concepts in mathematics. By understanding fractions, percentages, decimals, and their interrelationships, we equip ourselves with essential tools applicable in various real-world situations. This seemingly small mathematical problem unlocks a gateway to a deeper understanding of numbers and their applications in our daily lives. Mastering this fundamental concept is a crucial step toward achieving stronger numeracy skills and confidently tackling more complex mathematical challenges in the future. The ability to quickly and accurately calculate fractions like one-quarter is not just a mathematical skill; it's a practical life skill with far-reaching benefits.
Latest Posts
Latest Posts
-
What Is 25 25
Sep 24, 2025
-
6 5 5 6
Sep 24, 2025
-
Signs Of Secure Attachment
Sep 24, 2025
-
Number Line To 10
Sep 24, 2025
-
18 Km Per Hour
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 Quarter Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.