10 12 In Percentage
renascent
Sep 14, 2025 · 5 min read
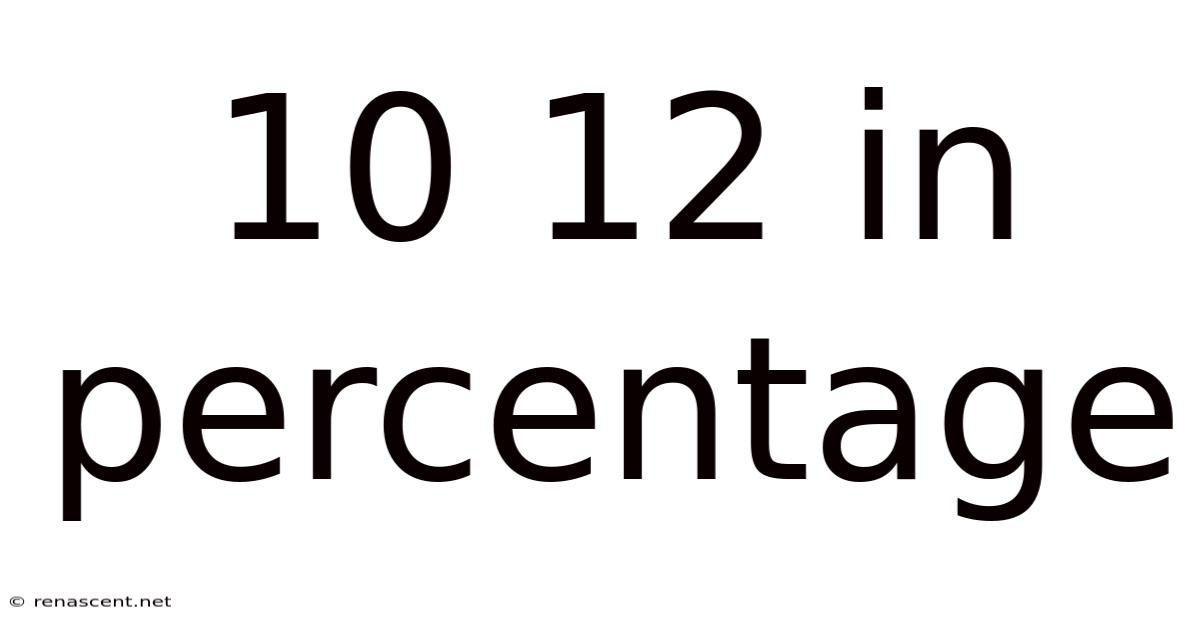
Table of Contents
Decoding 10/12 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating grades to understanding financial data. This article provides a comprehensive guide on converting the fraction 10/12 into a percentage, exploring the underlying concepts, providing step-by-step instructions, and addressing common questions. We'll delve into the process, exploring different methods and emphasizing the practical implications of understanding percentage calculations. This will empower you to confidently tackle similar fraction-to-percentage conversions in the future.
Understanding Fractions and Percentages
Before diving into the conversion of 10/12, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts in the whole.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates how many parts out of 100 constitute a specific portion of the whole. For example, 50% means 50 out of 100, which simplifies to 1/2.
The key to converting a fraction to a percentage is to express the fraction as an equivalent fraction with a denominator of 100. Then, the numerator of this equivalent fraction represents the percentage.
Method 1: Converting 10/12 to a Percentage via Division
The most straightforward method to convert 10/12 into a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (10) by the denominator (12).
10 ÷ 12 = 0.8333... (the 3s repeat infinitely)
-
Convert the decimal to a percentage: Multiply the decimal by 100.
0.8333... × 100 = 83.33...%
Therefore, 10/12 is approximately 83.33%. The repeating decimal indicates that the percentage is not perfectly precise, but 83.33% is a sufficiently accurate representation for most practical purposes.
Method 2: Simplifying the Fraction Before Conversion
Often, simplifying the fraction before conversion can make the calculations easier. Let's simplify 10/12:
Both 10 and 12 are divisible by 2. Simplifying, we get:
10/12 = 5/6
Now, we can convert 5/6 to a percentage using the division method:
-
Convert the fraction to a decimal: 5 ÷ 6 = 0.8333...
-
Convert the decimal to a percentage: 0.8333... × 100 = 83.33...%
This confirms that 10/12, simplified to 5/6, is approximately 83.33%. Simplifying the fraction beforehand doesn't change the final result but can streamline the calculation process, especially with larger numbers.
Method 3: Using Proportions
A less common but equally valid method utilizes proportions. We set up a proportion where x represents the percentage we're looking for:
10/12 = x/100
To solve for x, we cross-multiply:
12x = 1000
x = 1000/12
x ≈ 83.33
Therefore, 10/12 is approximately 83.33%. This method reinforces the underlying principle of percentages as a proportion out of 100.
Understanding the Recurring Decimal
The recurring decimal 0.8333... in the previous calculations is important to note. It signifies that the fraction 10/12 (or 5/6) cannot be expressed exactly as a finite decimal. The 3s repeat infinitely. For practical purposes, we round the decimal to a certain number of decimal places (e.g., 0.833 or 0.83), resulting in an approximation of the percentage. The level of precision needed will depend on the context. In many situations, rounding to two decimal places (83.33%) is sufficient.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in various real-world scenarios:
- Academic Grades: If a student answers 10 out of 12 questions correctly on a test, their score is 83.33%.
- Financial Calculations: Percentage changes in stock prices, interest rates, and discounts are frequently encountered.
- Data Analysis: Representing data as percentages often enhances clarity and comparison.
- Sales and Marketing: Discounts are often expressed as percentages (e.g., a 20% discount).
- Scientific Research: Presenting data in terms of percentages helps to communicate findings effectively.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert 10/12 to a percentage?
A1: Yes, absolutely! Most calculators have a percentage function. Simply divide 10 by 12 and then multiply by 100 to obtain the percentage.
Q2: Is 83.33% the exact percentage equivalent of 10/12?
A2: No, it's an approximation. The exact equivalent involves a repeating decimal (83.333...), which continues infinitely. 83.33% is a sufficiently accurate representation for most practical applications.
Q3: What if I have a more complex fraction to convert to a percentage?
A3: The same principles apply. Divide the numerator by the denominator and multiply the result by 100. You can simplify the fraction first to make calculations easier.
Q4: Why is understanding percentages important?
A4: Percentages provide a standardized way to compare proportions and fractions. They are universally understood and easily interpreted, making them essential in various fields.
Q5: How do I round a percentage correctly?
A5: Standard rounding rules apply. If the digit after the desired decimal place is 5 or greater, round up; if it's less than 5, round down. For example, 83.333...% rounded to two decimal places is 83.33%.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with practical applications across numerous disciplines. We've explored three methods for converting 10/12 to a percentage, emphasizing the importance of understanding the underlying concepts, including the implications of recurring decimals. This comprehensive guide equips you with the knowledge and techniques to confidently tackle similar conversions in the future, enhancing your mathematical proficiency and problem-solving abilities. Remember that practice is key; the more you work with these conversions, the more comfortable and proficient you'll become. So, grab a calculator, some practice problems, and start honing your skills!
Latest Posts
Latest Posts
-
Coca Cola Is Green
Sep 14, 2025
-
Molecular Mass Of Silver
Sep 14, 2025
-
Bird And Cage Tattoo
Sep 14, 2025
-
53 5 Kg To Lbs
Sep 14, 2025
-
1 53 Meters To Feet
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10 12 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.