10/15 As A Percent
renascent
Sep 22, 2025 · 5 min read
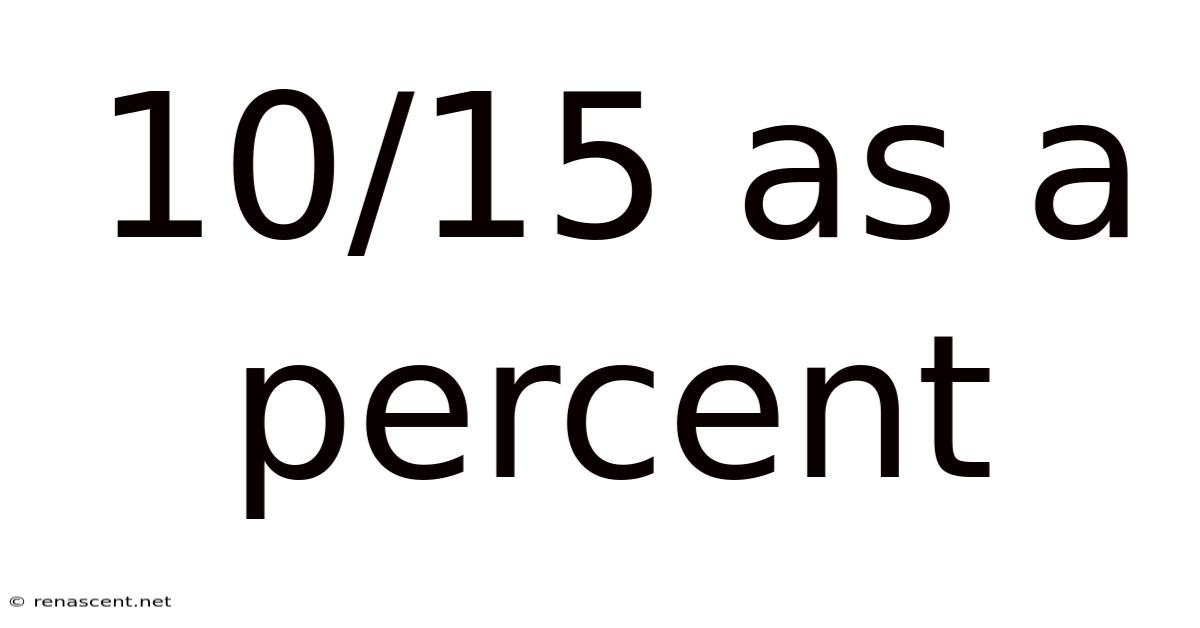
Table of Contents
Understanding 10/15 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistical data and financial reports. This article will delve into the process of converting the fraction 10/15 into a percentage, providing a step-by-step guide, exploring the underlying mathematical principles, and answering frequently asked questions. We'll also explore the broader context of fraction-to-percentage conversions and their real-world relevance. By the end, you'll not only know the answer but also understand the "why" behind the calculation.
Understanding Fractions and Percentages
Before we jump into converting 10/15, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. The top number (10 in this case) is called the numerator, representing the number of parts we have. The bottom number (15) is the denominator, representing the total number of parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction out of 100. It essentially expresses a proportion as a fraction of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 10/15 to a Percentage: Step-by-Step Guide
There are two main methods to convert 10/15 to a percentage:
Method 1: Simplifying the Fraction and then Converting
-
Simplify the Fraction: The fraction 10/15 can be simplified by finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 10 and 15 is 5. Dividing both the numerator and denominator by 5, we get:
10 ÷ 5 = 2 15 ÷ 5 = 3
This simplifies the fraction to 2/3.
-
Convert the Simplified Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator by the denominator:
2 ÷ 3 ≈ 0.6667 (We round to four decimal places for accuracy)
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.6667 × 100 = 66.67%
Therefore, 10/15 is equal to 66.67%.
Method 2: Direct Conversion using a Proportion
This method involves setting up a proportion:
-
Set up the Proportion: We want to find the percentage, which is a fraction out of 100. We can set up a proportion as follows:
10/15 = x/100
where 'x' represents the percentage we want to find.
-
Solve for x: To solve for x, we can cross-multiply:
15x = 1000
-
Isolate x: Divide both sides by 15:
x = 1000/15 ≈ 66.67
Therefore, x ≈ 66.67%, confirming our result from Method 1.
The Mathematical Principles Behind the Conversion
The core mathematical principle behind converting fractions to percentages lies in the concept of equivalent fractions. We are essentially finding an equivalent fraction where the denominator is 100. Multiplying both the numerator and the denominator of a fraction by the same number doesn't change its value; it only changes its representation. This is the foundation of both methods described above. Method 1 simplifies the fraction first to make the division easier, while Method 2 directly uses a proportion to find the equivalent fraction with a denominator of 100.
Real-World Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in numerous real-world scenarios:
-
Calculating Discounts: If a store offers a 20% discount on an item, understanding how this percentage relates to the original price is essential for calculating the final cost.
-
Understanding Tax Rates: Sales tax, income tax, and other taxes are often expressed as percentages. Knowing how to work with these percentages is crucial for managing personal finances.
-
Analyzing Statistical Data: Percentages are widely used to represent data in charts, graphs, and reports. Understanding how these percentages are derived from fractions helps in interpreting and drawing meaningful conclusions from the data.
-
Financial Calculations: Interest rates, investment returns, and other financial calculations often involve percentages.
-
Grading Systems: Many educational systems use percentages to represent student performance on assessments and assignments.
-
Recipe Scaling: If a recipe calls for a fraction of an ingredient, converting that fraction to a percentage can be useful for scaling the recipe up or down.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 10/15 to a percentage?
A: Yes, absolutely! Most calculators have a percentage function. Simply divide 10 by 15 and then multiply the result by 100.
Q: What if the fraction doesn't simplify easily?
A: Even if the fraction doesn't simplify easily, you can still use either of the methods described above. Method 2, using proportions, is particularly useful in such cases.
Q: Is there a difference between rounding to 66.67% and expressing it as a recurring decimal (66.666...%)?
A: Yes, there is a slight difference. 66.67% is an approximation, while 66.666...% is a more precise representation. The choice depends on the level of accuracy required. In most practical applications, 66.67% is sufficient.
Q: What if I have a mixed number instead of a simple fraction?
A: First, convert the mixed number into an improper fraction. Then, follow the steps outlined above to convert the improper fraction to a percentage.
Q: Why is understanding percentage conversions important?
A: Percentage conversions are essential for comprehending and utilizing numerical data in a variety of fields, from finance and business to science and everyday life. It enhances problem-solving skills and allows for informed decision-making based on quantitative information.
Conclusion
Converting 10/15 to a percentage involves a straightforward process, whether you choose to simplify the fraction first or use a direct proportional method. The answer, approximately 66.67%, is not merely a numerical result but a representation of a part-to-whole relationship expressed as a fraction of 100. Understanding this conversion process is vital for navigating numerous aspects of daily life and professional endeavors. The ability to confidently convert fractions to percentages empowers you to interpret data, make informed decisions, and succeed in various academic and real-world scenarios. Remember that the methods discussed here are applicable to converting any fraction to a percentage, making this a versatile skill with lasting value.
Latest Posts
Latest Posts
-
Molecular Mass Of Ethane
Sep 22, 2025
-
Australia Longitude And Latitude
Sep 22, 2025
-
Hydrogen Gas Pop Test
Sep 22, 2025
-
Quotes From Hedda Gabler
Sep 22, 2025
-
1 2 Of 57
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 10/15 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.