10 Is 20 Of
renascent
Sep 15, 2025 · 5 min read
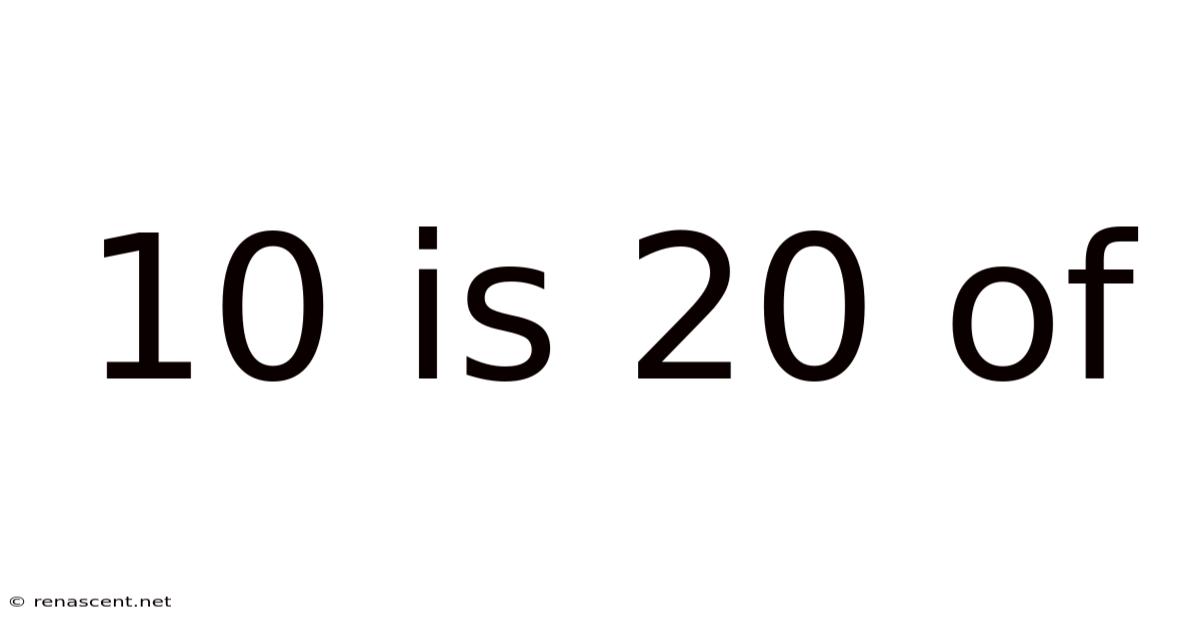
Table of Contents
Decoding the "10 is 20 of" Phenomenon: A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific calculations. This article will dissect the seemingly simple yet often confusing concept behind statements like "10 is 20% of," explaining the underlying mathematics and offering practical applications to solidify your grasp. We will explore the various ways to solve percentage problems, covering different scenarios and addressing common misconceptions. Mastering this will empower you to confidently tackle percentage-related challenges in your personal and professional life.
Understanding the Basics: What is a Percentage?
A percentage (%) represents a fraction of 100. It's a way to express a proportion or ratio as a part of a whole, where the whole is always considered to be 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal. This simple concept forms the basis for all percentage calculations.
The statement "10 is 20% of" implies a relationship between three values:
- The Part: This is the value representing a portion of the whole (in this case, 10).
- The Percentage: This is the ratio expressed as a percentage (20%).
- The Whole: This is the total value from which the part is derived (this is what we need to find).
Calculating "The Whole" When Given "The Part" and "The Percentage"
Let's break down how to solve the "10 is 20% of" problem. We are given:
- The Part: 10
- The Percentage: 20%
We need to find The Whole. We can set up an equation:
10 = 0.20 * x
where 'x' represents the whole. To solve for x, we simply divide both sides by 0.20 (the decimal equivalent of 20%):
x = 10 / 0.20
x = 50
Therefore, 10 is 20% of 50.
Different Approaches to Solving Percentage Problems
While the above method is straightforward, several other approaches can be used, depending on your preference and the complexity of the problem. Here are some alternative methods:
1. Using Proportions:
This method uses the concept of equivalent ratios. We can set up a proportion:
10/x = 20/100
Cross-multiplying gives:
10 * 100 = 20 * x
1000 = 20x
x = 1000 / 20
x = 50
2. Using the Formula:
A more general formula can be used to solve various percentage problems:
(Part / Whole) * 100 = Percentage
We can rearrange this formula to solve for any of the three variables. In our case, we want to find the Whole:
Whole = Part / (Percentage / 100)
Substituting the values:
Whole = 10 / (20/100)
Whole = 10 / 0.20
Whole = 50
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentage calculations. For instance, if a store offers a 25% discount on an item priced at $80, the discount amount would be 25% of $80, which is $20.
- Science: Many scientific measurements and analyses rely on percentages. For example, expressing the concentration of a solution, the efficiency of a process, or the error in an experiment.
- Statistics: Percentages are extensively used to represent data in surveys, polls, and research studies. For instance, showing the percentage of people who support a particular candidate in an election.
- Everyday Life: Calculating tips in restaurants, determining sale prices, understanding nutrition labels, and even figuring out the percentage of tasks completed in a project all use percentage calculations.
Common Mistakes to Avoid
Several common mistakes can lead to inaccurate percentage calculations:
- Incorrect Decimal Conversion: Failing to convert percentages to their decimal equivalents (e.g., 20% to 0.20) is a frequent error.
- Mixing Up Part and Whole: Confusing which value represents the part and which represents the whole can lead to incorrect answers.
- Incorrect Formula Application: Using the wrong formula or misinterpreting the formula can lead to errors.
- Rounding Errors: Rounding intermediate calculations prematurely can lead to significant inaccuracies in the final answer.
Advanced Percentage Calculations: Beyond the Basics
While "10 is 20% of" involves a relatively simple calculation, understanding percentages extends to more complex scenarios. These include:
- Percentage Increase/Decrease: Calculating the percentage change between two values. For example, if a quantity increases from 50 to 60, the percentage increase is [(60-50)/50] * 100 = 20%.
- Compound Interest: Calculating the accumulated value of an investment over time, considering the interest earned on both the principal and accumulated interest.
- Percentage Points: This is often misunderstood. A change of 10 percentage points is different from a 10% increase. For instance, if a value increases from 10% to 20%, this is a 10 percentage point increase but a 100% percentage increase.
Frequently Asked Questions (FAQ)
Q1: How do I calculate the percentage increase or decrease?
A1: To calculate the percentage increase or decrease, subtract the initial value from the final value, divide the result by the initial value, and then multiply by 100.
Q2: What's the difference between percentage and percentage points?
A2: Percentage points represent an absolute difference between two percentages, while percentage increase/decrease represents the relative change.
Q3: Can I use a calculator for percentage calculations?
A3: Yes, most calculators have percentage functions that simplify these calculations.
Q4: What are some resources for further learning about percentages?
A4: Many online resources, educational websites, and textbooks provide comprehensive explanations and practice problems on percentage calculations.
Conclusion: Mastering Percentages for a Brighter Future
Mastering percentage calculations is an invaluable skill that opens doors to numerous opportunities. From navigating personal finances to tackling complex scientific problems, understanding percentages empowers you to make informed decisions and solve real-world challenges. By understanding the underlying principles, employing different calculation methods, and avoiding common errors, you can confidently tackle any percentage problem, transforming seemingly daunting tasks into manageable achievements. This article serves as a stepping stone – continue to practice and explore further resources to build a strong foundation in this essential mathematical concept. Remember, practice makes perfect!
Latest Posts
Latest Posts
-
Head Covering Crossword Clue
Sep 15, 2025
-
115 Km To Mph
Sep 15, 2025
-
Oldest Sport In World
Sep 15, 2025
-
Draco Malfoy Yule Ball
Sep 15, 2025
-
Louis Henry Sullivan Architecture
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 10 Is 20 Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.