10 Of 250 000
renascent
Sep 19, 2025 · 6 min read
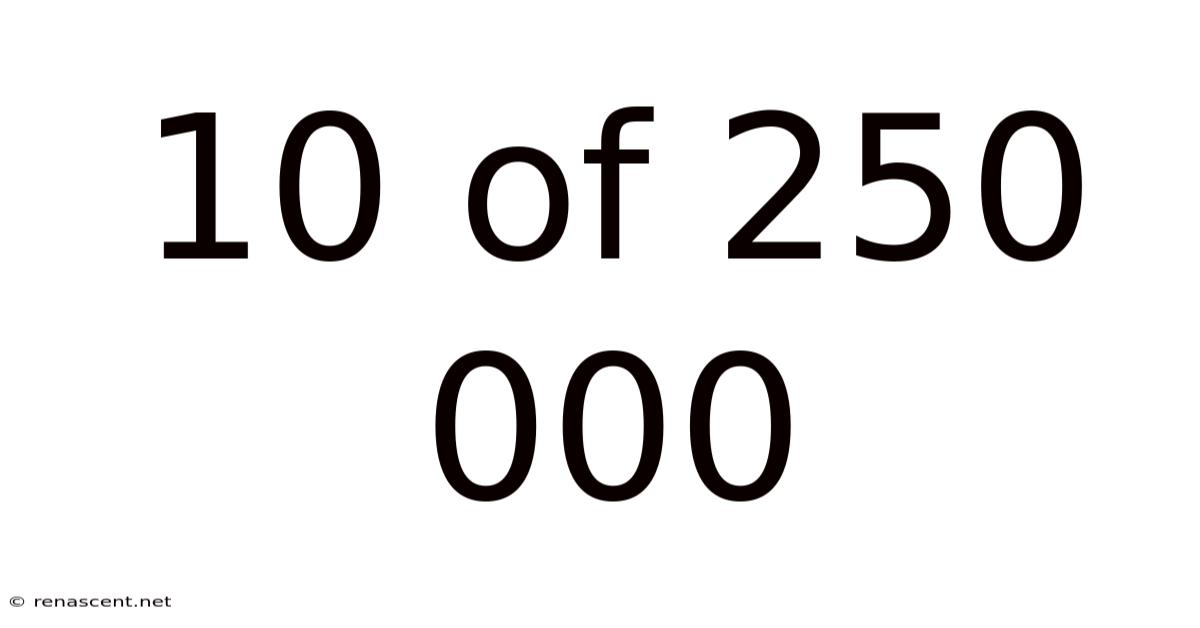
Table of Contents
Decoding the Infinitesimal: Exploring the Significance of 10 out of 250,000
Understanding the true meaning and implications of a seemingly small fraction, like 10 out of 250,000, requires moving beyond simply stating the ratio. This article delves deep into the interpretation of such a fraction, exploring its statistical significance, practical applications, and the broader implications of understanding relative proportions in various contexts. We'll examine how context drastically alters the significance of this number, from a medical trial to a lottery win, and highlight the importance of clear communication when dealing with such small proportions.
Introduction: The Power of Perspective
The fraction 10/250,000 represents a tiny percentage – 0.004% – a number that might initially seem insignificant. However, the true weight of this figure depends entirely on the context. A seemingly minuscule percentage can hold enormous significance depending on what it represents. This article explores different scenarios to illustrate how the interpretation shifts dramatically based on the underlying situation. We will use this specific example to illustrate the importance of numerical literacy and clear communication of statistical data.
1. Statistical Significance and Hypothesis Testing
In the realm of statistics, 10 out of 250,000 could represent a significant finding, especially in a controlled experiment. Imagine a clinical trial testing a new drug. If 10 out of 250,000 participants experienced a specific adverse reaction, this would likely prompt further investigation. While the percentage seems small, the absolute number of adverse events, in the context of a clinical trial, could be considered statistically significant, especially if the baseline rate of that adverse reaction in the placebo group was significantly lower. This significance would hinge on the use of statistical tests like chi-squared tests or Fisher's exact tests to determine the probability of observing this many adverse events by chance alone. A low p-value (typically below 0.05) would suggest a statistically significant association between the drug and the adverse reaction, demanding further scrutiny.
2. Risk Assessment and Probability
Consider a risk assessment scenario. If 10 out of 250,000 individuals in a specific population developed a rare disease, understanding this ratio is crucial. Public health officials would need to assess whether this number represents a significant increase in disease incidence compared to historical data. This necessitates a thorough epidemiological investigation, considering factors like age, geographic location, and potential environmental exposures. The low percentage, in this context, doesn't diminish the seriousness of the situation; rather, it highlights the need for careful investigation and proactive public health measures.
3. Quality Control and Manufacturing
In manufacturing, even a small defect rate can have significant economic implications. If a company produces 250,000 units and 10 are found to be defective, the 0.004% defect rate might seem insignificant. However, depending on the cost of repair or replacement, and the potential for product recalls or reputational damage, this small percentage could translate to substantial financial losses. Stringent quality control measures are necessary to minimize even small defect rates.
4. Lottery Wins and Probability Calculations
Consider the opposite scenario: a lottery. If there are 250,000 lottery tickets sold and 10 win a prize, your chances of winning are still extremely low, despite it seeming like a larger number of winners than we would normally expect. Understanding the probability (10/250,000) helps manage expectations. Even if the number of winners seems high relative to a smaller lottery pool, this fraction still represents an incredibly low probability of winning.
5. The Importance of Context and Clear Communication
This illustration emphasizes the importance of presenting statistical data clearly and accurately. Simply stating "10 out of 250,000" without context is meaningless. The significance of this number is entirely dependent on the context in which it's presented. For example, stating that 10 out of 250,000 people experienced a serious side effect from a drug is vastly different than stating that 10 out of 250,000 lottery tickets won. Clear communication necessitates:
- Specificity: Defining the population and the event being measured is crucial.
- Relative Risk: Comparing the rate to a baseline or control group allows for a better understanding of significance.
- Visual Aids: Charts and graphs can make complex data more accessible and understandable.
- Plain Language: Avoiding technical jargon makes the information understandable for a wider audience.
6. The Limitations of Simple Percentages
While percentages are useful for summarizing data, they have limitations. Using only a simple percentage like 0.004% overlooks the absolute numbers. In some cases, even a small percentage applied to a large population can represent a substantial number of individuals. This is crucial in understanding public health issues where even a small percentage of a large population can still represent a considerable number of affected individuals.
7. Expanding the Understanding: Proportions and Ratios
Understanding 10/250,000 means understanding the underlying concepts of proportions and ratios. This fraction can be simplified to 1/25,000, offering a clearer representation of the relationship between the two numbers. This simplification allows for easier comparisons and calculations in various contexts.
8. Beyond the Numbers: Qualitative Aspects
While quantitative analysis is crucial, it's also important to consider qualitative aspects. For instance, in the clinical trial example, the severity of the adverse reaction is as crucial as the number of occurrences. A small percentage of life-threatening adverse reactions is far more concerning than a larger percentage of minor side effects. Similarly, in quality control, the type of defect influences the significance of the defect rate. A minor cosmetic defect is less concerning than a critical functional failure.
9. The Role of Sampling and Estimation
Often, 250,000 might represent a sample from a larger population. In such cases, the observed 10 occurrences must be interpreted within the context of the sampling process. Statistical methods are used to estimate the true proportion in the larger population, considering the margin of error associated with sampling. Confidence intervals provide a range of plausible values for the true proportion, accounting for the uncertainty inherent in sampling.
10. Applications Across Disciplines
Understanding the implications of 10/250,000 extends far beyond the examples discussed. It applies to various fields:
- Ecology: Studying rare species populations and conservation efforts.
- Finance: Analyzing investment risks and returns.
- Sociology: Examining social trends and demographics.
- Computer Science: Analyzing algorithm efficiency and error rates.
In each of these contexts, grasping the relative significance of a small fraction like 10/250,000 is essential for informed decision-making and effective problem-solving.
Conclusion: The Art of Contextual Interpretation
The simple fraction 10/250,000, seemingly insignificant on its own, showcases the critical role of context in interpreting numerical data. Its significance is not inherent in the numbers themselves but arises from the specific situation they describe. By understanding the statistical implications, considering the relevant factors, and communicating findings clearly, we can effectively leverage such seemingly small proportions to draw meaningful conclusions and make informed decisions across a multitude of disciplines. The ability to interpret such fractions is a cornerstone of critical thinking and numerical literacy, skills essential for navigating the complexities of our data-driven world. Furthermore, this analysis highlights the importance of moving beyond a superficial understanding of percentages to a deeper grasp of proportions, ratios, and the underlying statistical principles that shape their interpretation. Only through this comprehensive approach can we truly unlock the power of seemingly insignificant numbers.
Latest Posts
Latest Posts
-
380 Minutes To Hours
Sep 19, 2025
-
Emission Spectra Of Neon
Sep 19, 2025
-
1 50 As Decimal
Sep 19, 2025
-
The Evil Of Banality
Sep 19, 2025
-
34 As A Decimal
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 250 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.