10 Percent Of 300
renascent
Sep 14, 2025 · 5 min read
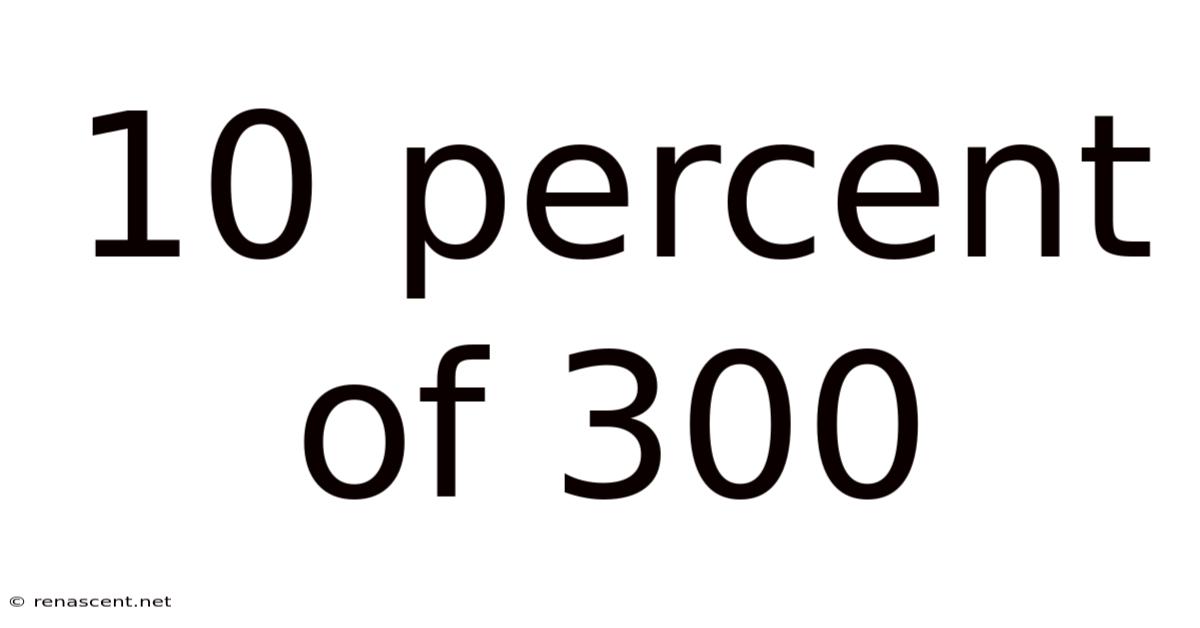
Table of Contents
Decoding 10 Percent of 300: A Deep Dive into Percentages and Their Applications
Finding 10 percent of 300 might seem like a simple task, a quick calculation for a seasoned mathematician. But for those just beginning their journey into the world of percentages, or even those looking for a refresher on fundamental mathematical concepts, understanding this seemingly simple problem unlocks a wealth of knowledge applicable across various fields. This article will not only provide the answer but delve into the methods used to calculate percentages, explore the real-world applications of percentage calculations, and address frequently asked questions. Understanding percentages is crucial for everyday life, from calculating discounts and taxes to comprehending financial statements and statistical data.
Understanding Percentages: The Foundation
Before diving into the specific calculation of 10 percent of 300, let's establish a firm grasp of the concept of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per cent," or "out of 100." Therefore, 10% can be expressed as the fraction 10/100, or the decimal 0.10. This fundamental understanding is crucial for all percentage calculations.
Method 1: The Decimal Method – Calculating 10% of 300
This is arguably the most straightforward method. As mentioned above, 10% is equivalent to 0.10. Therefore, to find 10% of 300, we simply multiply 300 by 0.10:
300 * 0.10 = 30
Therefore, 10 percent of 300 is $\boxed{30}$.
This method is efficient and easily adaptable to different percentages. For example, to find 25% of 300, you would multiply 300 by 0.25 (25/100).
Method 2: The Fraction Method – A Different Perspective
Another approach involves using fractions. We know that 10% is equivalent to the fraction 10/100. This fraction can be simplified to 1/10. Therefore, finding 10% of 300 is the same as finding one-tenth of 300:
300 * (1/10) = 300/10 = 30
This method highlights the relationship between percentages and fractions, offering a more intuitive understanding of the calculation. It's particularly helpful when dealing with percentages that easily translate to simple fractions, such as 25% (1/4), 50% (1/2), or 75% (3/4).
Method 3: The Proportion Method – Setting up an Equation
This method is useful for solving more complex percentage problems. We can set up a proportion:
Let x be 10% of 300.
10/100 = x/300
To solve for x, we cross-multiply:
10 * 300 = 100 * x
3000 = 100x
x = 3000/100
x = 30
This method is more formal and can be applied to a wider range of percentage problems, including those where the percentage or the whole amount is unknown. It's a valuable tool for developing a deeper understanding of percentage relationships.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is not just an academic exercise; it’s a vital life skill with wide-ranging applications:
- Shopping and Sales: Calculating discounts (e.g., a 20% off sale), sales tax, and tip amounts are all based on percentage calculations.
- Finance: Understanding interest rates on loans and savings accounts, analyzing financial statements, calculating returns on investments, and comprehending tax brackets all heavily rely on percentages.
- Statistics and Data Analysis: Percentages are frequently used to represent data in charts, graphs, and reports, allowing for easy comparison and interpretation of trends and patterns. For example, understanding unemployment rates, population growth, and survey results often involves working with percentages.
- Science and Engineering: Percentage calculations are employed in numerous scientific and engineering applications, such as calculating efficiency, error rates, and concentration levels.
- Everyday Life: From understanding nutritional information on food labels (e.g., percentage of daily value) to calculating the percentage of completion on a project, percentages are integral to our daily lives.
Beyond the Basics: Extending Percentage Understanding
While calculating 10% of 300 is relatively simple, the principles involved open doors to more complex calculations:
- Calculating the Percentage Increase or Decrease: Determining the percentage change between two numbers is a common application. For example, if a price increases from 300 to 330, the percentage increase is calculated as follows: [(330 - 300) / 300] * 100% = 10%.
- Finding the Original Amount: If you know the percentage and the final amount after a percentage increase or decrease, you can work backward to find the original amount.
- Working with Multiple Percentages: Many real-world scenarios involve applying multiple percentages consecutively. For instance, calculating the final price after a discount and then adding sales tax requires understanding the order of operations and the cumulative effect of these percentages.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a different percentage of 300?
A1: Use the decimal method or the fraction method, adapting the decimal or fraction equivalent of the desired percentage. For instance, to find 25% of 300, multiply 300 by 0.25 (or use the fraction 1/4).
Q2: How can I calculate percentages without a calculator?
A2: For simple percentages like 10%, 25%, 50%, and 75%, the fraction method is efficient. For other percentages, mental math techniques and approximation can be useful. Breaking down complex percentages into simpler components can also be helpful.
Q3: What are some common mistakes to avoid when calculating percentages?
A3: Common errors include incorrectly converting percentages to decimals, misplacing the decimal point, and incorrectly applying the order of operations when multiple percentages are involved. Double-checking your work and using different methods to verify your answer is always recommended.
Q4: Are there any online tools or calculators available for percentage calculations?
A4: While this article avoids external links, numerous online percentage calculators are readily available. These can be useful for verifying your calculations or for handling more complex percentage problems.
Conclusion: Mastering Percentages – A Valuable Skill
Calculating 10% of 300, while a seemingly simple problem, serves as a gateway to a broader understanding of percentages and their applications. Mastering percentage calculations is essential for navigating various aspects of daily life, from personal finance to professional endeavors. By understanding the different methods and their underlying principles, you'll not only be able to solve percentage problems efficiently but also develop a deeper appreciation for the power and versatility of this fundamental mathematical concept. The ability to confidently work with percentages empowers you to make informed decisions, analyze data effectively, and tackle more complex mathematical challenges with ease. Remember to practice regularly and explore different methods to solidify your understanding and build your confidence.
Latest Posts
Latest Posts
-
26 Divided By 30
Sep 14, 2025
-
2 Mg To Micrograms
Sep 14, 2025
-
6 7 In Decimal Form
Sep 14, 2025
-
Is Not About Money
Sep 14, 2025
-
Female Names In Argentina
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10 Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.