100 Divided By 24
renascent
Sep 15, 2025 · 6 min read
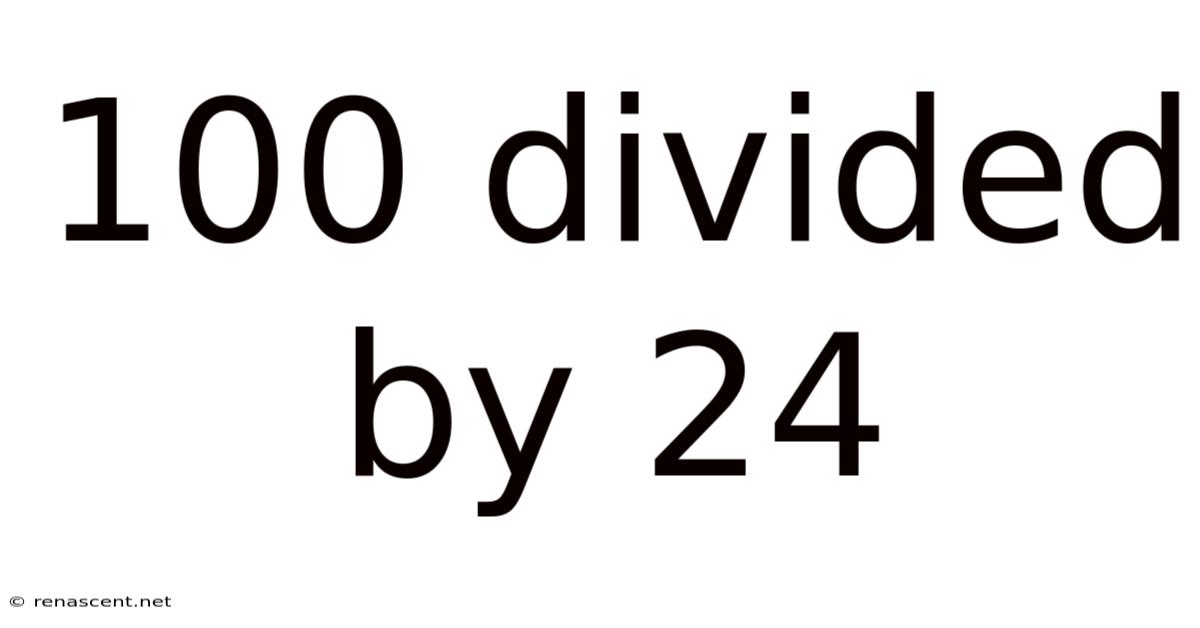
Table of Contents
Unveiling the Mystery: 100 Divided by 24 – A Deep Dive into Division and its Applications
Have you ever found yourself grappling with a seemingly simple division problem, only to discover a surprising complexity hidden beneath the surface? The seemingly straightforward calculation of 100 divided by 24 is a perfect example. This article will delve into the intricacies of this calculation, exploring various methods of solving it, unpacking the resulting decimal, and showcasing the practical applications of this type of division problem in everyday life and various fields. Understanding this seemingly simple problem unlocks a deeper appreciation for the power and versatility of mathematics.
Understanding the Basics: Division and its Components
Before we tackle 100 divided by 24, let's refresh our understanding of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the expression 100 ÷ 24 (or 100/24), 100 is the dividend (the number being divided), 24 is the divisor (the number by which we divide), and the result is the quotient. In this specific case, we will also encounter a remainder, which represents the portion of the dividend that cannot be equally divided by the divisor.
Method 1: Long Division – The Classic Approach
The traditional method of solving 100 divided by 24 is through long division. This method, while seemingly tedious, provides a step-by-step process that allows for a clear understanding of the division process and the generation of both the quotient and remainder.
-
Set up the problem: Write 100 as the dividend inside the long division symbol and 24 as the divisor outside.
-
Determine the first digit of the quotient: Ask yourself, "How many times does 24 go into 10?" The answer is zero. So, we move to the next digit, making it "100". How many times does 24 go into 100? The answer is 4. Write 4 above the 0 in 100.
-
Multiply and subtract: Multiply the divisor (24) by the digit we just placed in the quotient (4). 24 x 4 = 96. Subtract 96 from 100. 100 - 96 = 4. This 4 is the remainder.
Therefore, 100 divided by 24 is 4 with a remainder of 4. We can express this as 4 R 4.
Method 2: Decimal Division – Beyond the Whole Number
While the remainder approach is suitable in certain contexts, many situations require a decimal representation of the quotient. To obtain the decimal equivalent, we continue the long division process by adding a decimal point and zeros to the dividend.
-
Add a decimal point and zeros: After obtaining the remainder 4, add a decimal point to the dividend (100) and add zeros as needed. This gives us 4.000…
-
Continue the division: Bring down a zero. Now we have 40. How many times does 24 go into 40? It goes once (1). Place the 1 after the decimal point in the quotient.
-
Repeat the process: Multiply 24 by 1 (24), and subtract it from 40 (40 - 24 = 16). Bring down another zero (160). 24 goes into 160 six times (24 x 6 = 144). Subtract 144 from 160, leaving a remainder of 16.
-
Iterate for accuracy: This process can be continued to obtain a more precise decimal representation. By adding more zeros and continuing the division, we will find the quotient approaches 4.16666... This is a recurring decimal, indicated by the repeating 6.
Therefore, 100 divided by 24 ≈ 4.1667 (rounded to four decimal places).
Method 3: Using a Calculator – The Convenient Approach
In the modern era, calculators provide a quick and efficient way to perform division calculations. Simply enter 100 ÷ 24 and press the equals button. The calculator will swiftly display the decimal result: approximately 4.1666666667. This confirms our results from the long division method.
Understanding the Decimal Result: Recurring Decimals and Fractions
The decimal result, approximately 4.16666..., is a recurring decimal, meaning a digit or a sequence of digits repeats infinitely. In this case, the digit 6 repeats indefinitely. This recurring decimal can also be represented as a fraction.
To convert the decimal to a fraction, we can use the following method:
-
Identify the repeating part: The repeating part is 6.
-
Express as a fraction: The repeating decimal 0.16666... can be represented as 1/6. Then add the whole number 4 to get the final fraction. The mixed fraction equivalent of 4.1666... is 4 1/6, or the improper fraction 25/6
Real-World Applications: Where This Calculation Matters
The seemingly simple calculation of 100 divided by 24 has numerous practical applications in various fields:
-
Resource Allocation: Imagine dividing 100 resources (e.g., budget, materials, or personnel) among 24 teams. The calculation helps determine the allocation per team and potential leftover resources.
-
Unit Conversion: In various engineering and scientific applications, converting between different units often involves division. For example, converting 100 centimeters into meters (100 cm / 24 cm/meter).
-
Rate Calculation: Determining an average rate based on total units and available time often involves division. For instance, calculating average speed if you traveled 100 kilometers in 24 hours.
-
Statistical Analysis: In statistical computations, division is a fundamental operation in calculating means, medians, and other descriptive statistics.
-
Financial Calculations: Dividing profits among shareholders, calculating interest rates, and determining per-unit cost all depend on division.
-
Proportion and Ratio Problems: Dividing a quantity according to a given ratio utilizes the concept of division.
-
Baking and Cooking: Adjusting recipes to serve more or fewer people often involves scaling up or down, which requires the use of division.
Frequently Asked Questions (FAQ)
Q: Can 100 divided by 24 be expressed as a whole number?
A: No, 100 divided by 24 cannot be expressed as a whole number because 100 is not perfectly divisible by 24. There will always be a remainder.
Q: What is the most accurate way to represent the result of 100 divided by 24?
A: The most accurate representation is as a fraction (25/6) or a recurring decimal (4.1666...). Rounding to a specific number of decimal places depends on the required level of precision for the application.
Q: Why is understanding the remainder important?
A: Understanding the remainder is crucial in scenarios where resources cannot be split into fractional parts. For example, you cannot divide 100 apples equally among 24 people; there will be a remainder of 4 apples.
Q: What are some alternative methods to calculate 100 divided by 24?
A: Besides long division and calculators, other approaches include using software programs or online division tools.
Conclusion: The Power of Understanding Division
The seemingly simple problem of 100 divided by 24 illustrates the broader importance of understanding fundamental mathematical operations. From the traditional method of long division to the convenience of calculators, multiple approaches can lead to the same result. By comprehending the process, the resulting decimal, and the different ways to represent the solution, we gain a deeper appreciation for the versatile nature of mathematics and its practical applications in a multitude of situations. This understanding extends beyond simple calculations to build a stronger foundation for more complex mathematical concepts and problem-solving in various fields. Remember, even seemingly basic calculations hold a wealth of knowledge and power when explored in depth.
Latest Posts
Latest Posts
-
Dancing Rabbit Creek Treaty
Sep 15, 2025
-
174 Cm To Height
Sep 15, 2025
-
205 Lb To Kg
Sep 15, 2025
-
5 9 As Decimal
Sep 15, 2025
-
3 66 Kg In Pounds
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 100 Divided By 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.