100 Divided By 7
renascent
Sep 17, 2025 · 6 min read
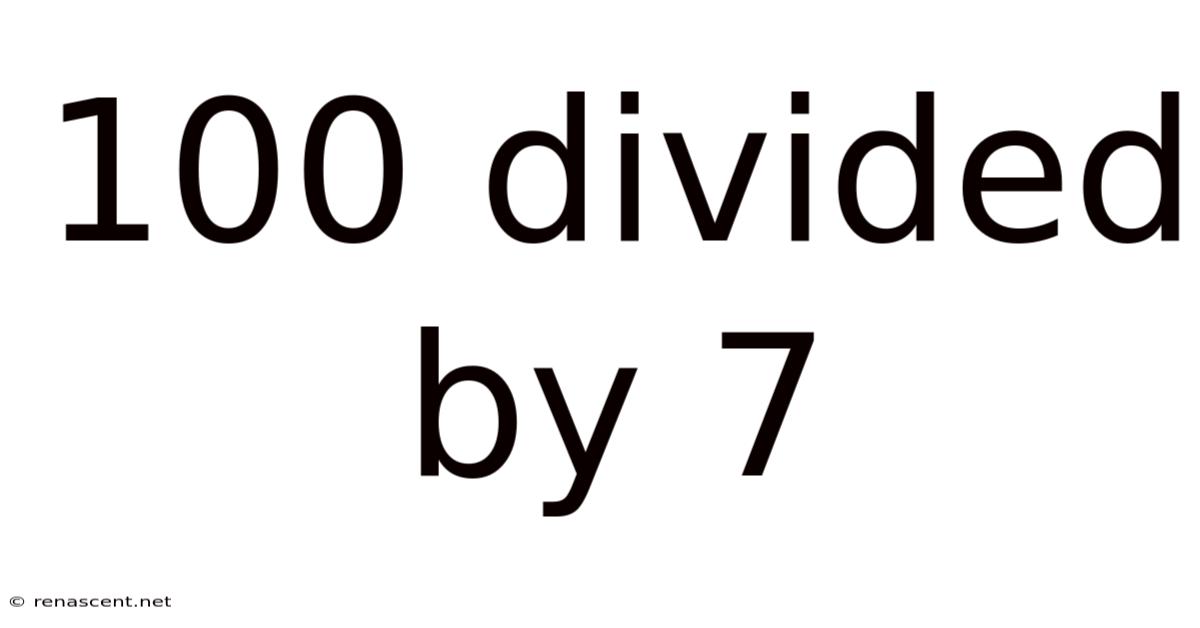
Table of Contents
100 Divided by 7: Exploring Division, Remainders, and Real-World Applications
Dividing 100 by 7 might seem like a simple arithmetic problem, but it opens a door to understanding fundamental mathematical concepts with far-reaching applications. This seemingly straightforward calculation introduces us to the concepts of division, remainders, decimals, and fractions, all crucial building blocks for more advanced mathematical explorations. This article will delve into the intricacies of 100 divided by 7, providing a comprehensive understanding for learners of all levels.
Understanding the Division Process
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of finding out how many times one number (the divisor) goes into another number (the dividend). In our case, we're dividing 100 (the dividend) by 7 (the divisor).
The simplest way to approach this problem is through long division. Let's break down the process step-by-step:
-
Set up the long division: Write 100 inside the long division symbol and 7 outside.
-
Divide: Ask yourself, "How many times does 7 go into 1?" It doesn't. Then, consider "How many times does 7 go into 10?" It goes once (7 x 1 = 7). Write the '1' above the '0' in 100.
-
Multiply: Multiply the quotient (1) by the divisor (7): 1 x 7 = 7. Write this below the '10'.
-
Subtract: Subtract the result (7) from the '10': 10 - 7 = 3.
-
Bring down: Bring down the next digit from the dividend (0), placing it next to the 3, making it 30.
-
Repeat: Ask, "How many times does 7 go into 30?" It goes four times (7 x 4 = 28). Write the '4' above the '0' in 100.
-
Multiply: Multiply the quotient (4) by the divisor (7): 4 x 7 = 28. Write this below the 30.
-
Subtract: Subtract the result (28) from 30: 30 - 28 = 2.
-
Remainder: The '2' is the remainder. This means that 7 goes into 100 fourteen times with 2 left over.
Therefore, 100 divided by 7 is 14 with a remainder of 2. We can express this as: 100 ÷ 7 = 14 R 2.
Exploring Decimals and Fractions
While the remainder provides a complete answer in whole numbers, we can further refine our understanding by expressing the result as a decimal or a fraction.
Decimal Representation
To find the decimal representation, we continue the long division process beyond the whole number portion. After obtaining a remainder of 2, we add a decimal point to the dividend (100) and append zeros as needed.
-
Add a decimal point to the quotient (14) and continue dividing: 7 goes into 20 twice (7 x 2 = 14), leaving a remainder of 6.
-
Bring down another zero, making it 60. 7 goes into 60 eight times (7 x 8 = 56), leaving a remainder of 4.
-
Bring down another zero, making it 40. 7 goes into 40 five times (7 x 5 = 35), leaving a remainder of 5.
-
Continue this process as far as needed for the desired level of accuracy. The decimal representation will be a repeating decimal, approximately 14.2857142857...
Therefore, 100 divided by 7, expressed as a decimal, is approximately 14.2857. The sequence '285714' repeats infinitely.
Fractional Representation
The remainder can also be expressed as a fraction. The remainder (2) becomes the numerator, and the divisor (7) becomes the denominator. So, 100 divided by 7 can be written as a mixed number: 14 2/7. This means 14 whole units and 2/7 of another unit.
The Significance of Remainders
Remainders are not just leftover numbers; they hold significant meaning and utility in various contexts:
-
Grouping and Distribution: Imagine dividing 100 candies equally among 7 friends. Each friend gets 14 candies, and you have 2 candies left over.
-
Modular Arithmetic: Remainders are fundamental in modular arithmetic, a branch of number theory with applications in cryptography and computer science. The remainder when a number is divided by another is called the modulo operation (e.g., 100 mod 7 = 2).
-
Real-world Applications: Remainders show up in various real-world scenarios, such as scheduling, resource allocation, and even in certain aspects of physics and engineering. For example, consider dividing a length of 100 meters into segments of 7 meters. You'd have 14 segments with a 2-meter remainder.
Further Mathematical Explorations
The simple division of 100 by 7 opens doors to further exploration of related mathematical concepts:
-
Prime Numbers: The divisor (7) is a prime number, meaning it's only divisible by 1 and itself. Understanding prime numbers is crucial in number theory and cryptography.
-
Divisibility Rules: Exploring divisibility rules can help predict whether a number is divisible by another without performing long division. While there isn't a specific rule for divisibility by 7, some methods using modular arithmetic exist.
-
Factors and Multiples: Understanding factors and multiples enhances our comprehension of numerical relationships. 7 is a factor of numbers like 14, 21, 28 and 100 is a multiple of several numbers, such as 1, 2, 4, 5, 10, 20, 25, and 50.
-
Rational and Irrational Numbers: The decimal representation of 100/7 illustrates the concept of rational numbers (numbers expressible as a fraction of two integers) contrasted with irrational numbers (like π or √2), which have non-repeating, non-terminating decimal expansions.
Frequently Asked Questions (FAQ)
-
Q: What is the exact value of 100 divided by 7?
- A: The exact value is 14 with a remainder of 2, or 14 2/7 as a mixed number. The decimal representation is a repeating decimal approximately equal to 14.2857142857...
-
Q: Why does 100 divided by 7 result in a repeating decimal?
- A: Because the fraction 2/7, representing the remainder, cannot be expressed as a terminating decimal. The denominator (7) contains prime factors other than 2 and 5.
-
Q: Are there any shortcuts for dividing by 7?
- A: There aren't simple divisibility rules for 7 like there are for other numbers (e.g., 2, 3, 5, 10). Long division or using a calculator is generally the most efficient approach. However, some clever algorithms and tricks exist involving modular arithmetic, but they are beyond the scope of this basic introduction.
-
Q: What are some real-world applications of this calculation?
- A: Applications include resource allocation (sharing 100 items among 7 people), measurement conversions (dividing 100 meters into 7-meter segments), and scheduling problems (dividing 100 tasks across 7 days).
Conclusion
The seemingly simple problem of 100 divided by 7 reveals a rich tapestry of mathematical concepts, from fundamental division and remainders to the complexities of decimals, fractions, and modular arithmetic. Understanding this basic calculation builds a strong foundation for more advanced mathematical pursuits and provides valuable insights into real-world problem-solving. By exploring different representations of the answer – whole number with a remainder, decimal, and fraction – we gain a more profound understanding of the relationship between these core mathematical concepts. This exercise reinforces the significance of even seemingly simple calculations and their surprisingly broad applications across various fields. Remember, the journey of mathematical understanding is often found in the details, even the details of a simple division problem.
Latest Posts
Latest Posts
-
Look Up And Live
Sep 17, 2025
-
The Curious Incident Themes
Sep 17, 2025
-
Stardew Geologist Or Miner
Sep 17, 2025
-
76 5 Kg In Lbs
Sep 17, 2025
-
128 Divided By 4
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 100 Divided By 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.