11 25 As Percentage
renascent
Sep 25, 2025 · 5 min read
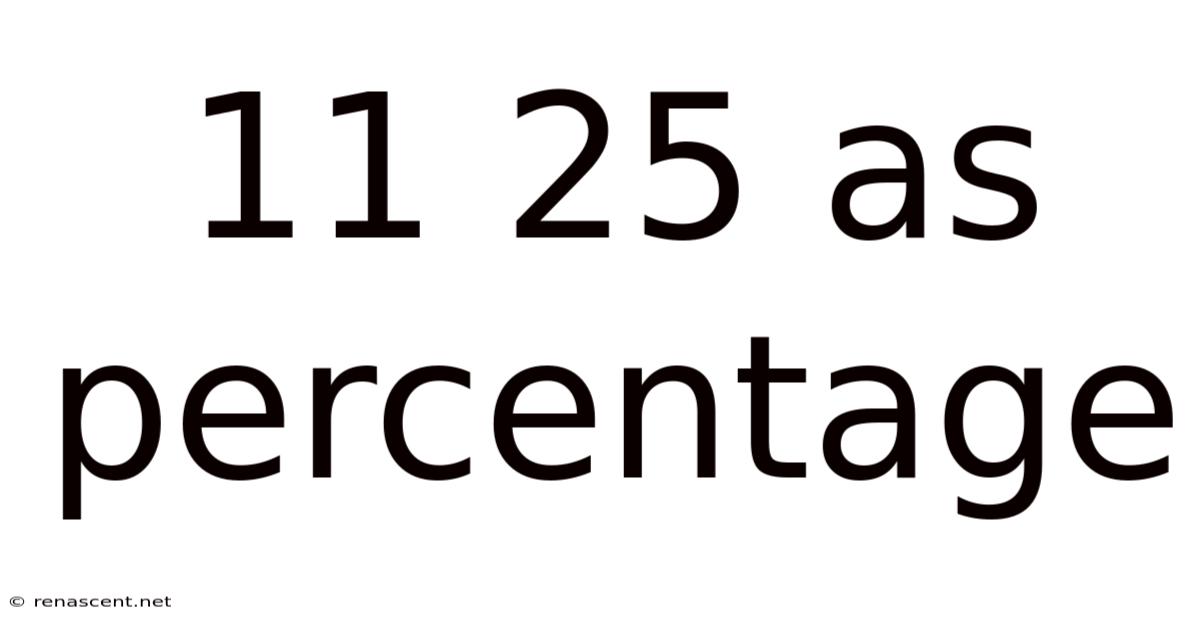
Table of Contents
Understanding 11/25 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistical data and financial reports. This article will thoroughly explain how to convert the fraction 11/25 into a percentage, providing a step-by-step guide, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also delve into practical examples to solidify your understanding. By the end, you'll not only know the answer but also possess a deeper understanding of percentage calculations.
Understanding Fractions and Percentages
Before we delve into the specific calculation of 11/25 as a percentage, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 11/25, 11 is the numerator and 25 is the denominator. This means we have 11 parts out of a total of 25 parts.
A percentage, on the other hand, is a way of expressing a fraction as a portion of 100. The term "percent" literally means "out of 100" (per centum in Latin). Percentages are often used because they provide a standardized and easily comparable way to represent proportions.
Method 1: Converting the Fraction to a Decimal Then to a Percentage
The most straightforward method for converting 11/25 to a percentage involves two steps:
-
Convert the fraction to a decimal: To do this, we simply divide the numerator (11) by the denominator (25):
11 ÷ 25 = 0.44
-
Convert the decimal to a percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%):
0.44 × 100 = 44%
Therefore, 11/25 is equal to 44%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This directly gives us the percentage because percentages are fractions out of 100.
To achieve this, we need to find a number that, when multiplied by the denominator (25), equals 100. In this case, that number is 4 (25 x 4 = 100). Crucially, whatever we do to the denominator, we must also do to the numerator to maintain the equivalence of the fraction.
-
Multiply both the numerator and denominator by 4:
(11 × 4) / (25 × 4) = 44/100
-
Express as a percentage: Since the denominator is now 100, the numerator directly represents the percentage:
44/100 = 44%
This method confirms that 11/25 is indeed 44%.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion where one ratio represents the given fraction (11/25) and the other ratio represents the unknown percentage (x/100).
-
Set up the proportion:
11/25 = x/100
-
Cross-multiply:
11 × 100 = 25 × x
-
Solve for x:
1100 = 25x x = 1100 / 25 x = 44
Therefore, x = 44, meaning 11/25 is 44%.
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages is crucial in numerous real-world scenarios. Here are a few examples:
- Discounts: If a store offers a 44% discount on an item, you can use this knowledge to quickly calculate the discount amount.
- Taxes: Sales tax is often expressed as a percentage. Knowing how to calculate percentages allows you to determine the total cost of an item including tax.
- Grades: Many educational systems use percentages to represent grades, making understanding fraction-to-percentage conversions essential for interpreting academic performance.
- Financial Analysis: Percentages are widely used in financial statements and reports to represent various ratios and metrics, providing insights into a company's financial health.
- Data Analysis: In statistics, percentages are frequently used to represent proportions within datasets, making comparisons and interpretations easier.
Further Exploration: Working with More Complex Fractions
While 11/25 is a relatively straightforward fraction to convert, the same principles apply to more complex fractions. If you encounter a fraction with a denominator that doesn't easily convert to 100, you can always use the first method (dividing the numerator by the denominator to get a decimal, then multiplying by 100 to get a percentage). Remember that using a calculator can significantly simplify the process, especially for fractions with larger numbers.
Frequently Asked Questions (FAQ)
-
Q: What if the decimal has more than two places after the decimal point?
A: When converting a decimal to a percentage, you multiply by 100. If the decimal has more than two decimal places, the resulting percentage will also have more than two decimal places. You may round the percentage to a reasonable number of decimal places depending on the context. For example, if you get 0.4444..., multiplying by 100 results in 44.444...%, which you might round to 44.44% or 44.4% depending on the level of precision required.
-
Q: Can I use a calculator to convert fractions to percentages?
A: Absolutely! Calculators are a helpful tool for these conversions, especially for fractions with larger numbers. Simply divide the numerator by the denominator and then multiply the result by 100.
-
Q: Why are percentages so useful?
A: Percentages offer a standardized way to compare proportions. It's much easier to compare 44% to 60% than to compare 11/25 to 3/5, for instance. This standardization makes them valuable in various fields.
-
Q: What if the fraction is an improper fraction (numerator > denominator)?
A: The same methods apply. Convert the improper fraction to a mixed number or decimal and then follow the steps outlined above. The resulting percentage will be greater than 100%.
Conclusion
Converting 11/25 to a percentage is a simple yet important skill. Whether you use the method of converting to a decimal first, finding an equivalent fraction with a denominator of 100, or utilizing proportions, the result remains the same: 44%. Understanding this conversion process extends beyond simple calculations; it's a foundation for grasping concepts in various fields requiring proportional reasoning. By mastering these methods, you equip yourself with a valuable tool for interpreting data and solving practical problems in numerous aspects of life. Remember to practice regularly to build confidence and fluency in your percentage calculations.
Latest Posts
Latest Posts
-
Define Inferior In Anatomy
Sep 25, 2025
-
Conservation Of Mass Experiment
Sep 25, 2025
-
Daughter Of The Forest
Sep 25, 2025
-
160 Km To Miles
Sep 25, 2025
-
Mating Donkeys And Horses
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 11 25 As Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.