11 Divided By 4
renascent
Sep 20, 2025 · 6 min read
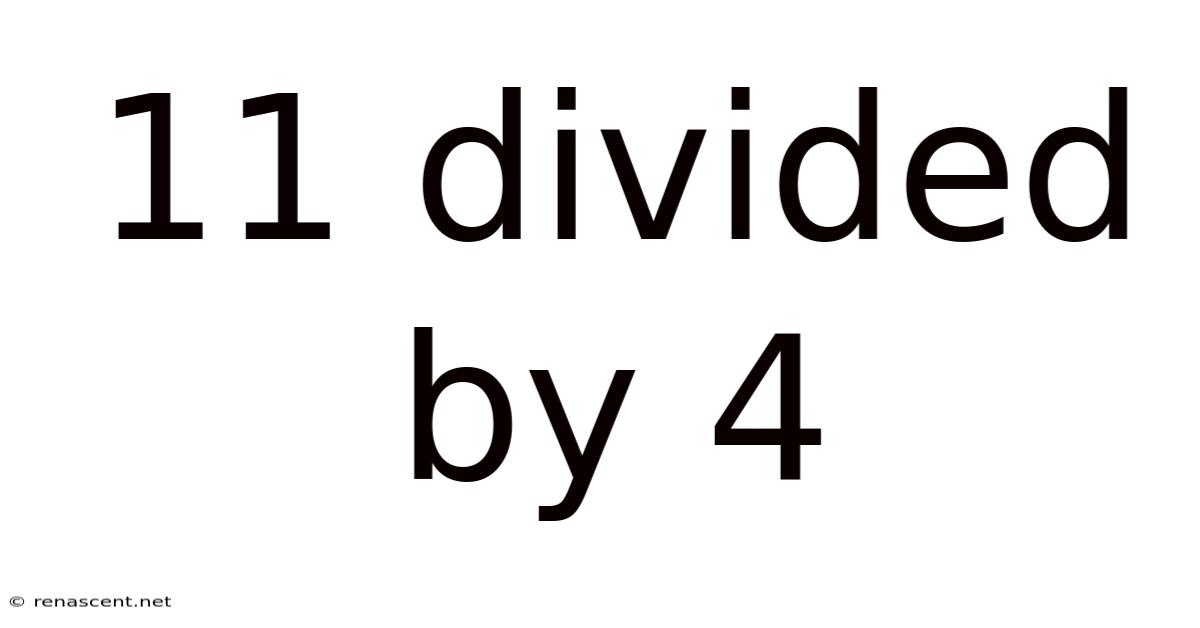
Table of Contents
Unveiling the Mystery: A Deep Dive into 11 Divided by 4
Dividing 11 by 4 might seem like a simple arithmetic problem, suitable only for elementary school students. However, a closer examination reveals a wealth of mathematical concepts and applications that extend far beyond basic division. This article will explore the intricacies of 11 ÷ 4, examining its various representations, practical applications, and the underlying mathematical principles that govern its solution. We'll delve into different approaches to solving this seemingly simple problem, moving beyond the immediate answer to uncover a deeper understanding of division and its significance in mathematics. This comprehensive guide is designed for anyone from students brushing up on their arithmetic to those curious about the elegance hidden within seemingly simple calculations.
Understanding the Problem: 11 ÷ 4
At its core, 11 ÷ 4 asks: "How many times does 4 fit into 11?" This question can be approached in several ways, each offering unique insights into the nature of division. The most straightforward approach involves performing long division, which we will explore in detail in the following section. However, it's crucial to understand that the answer isn't just a single number; it represents a quotient and a remainder, reflecting the incomplete nature of the division. This incomplete division leads to the concept of fractions and decimals, which we will also discuss.
Method 1: Long Division – A Step-by-Step Guide
Long division provides a systematic method for solving 11 ÷ 4. Let's break down the process step-by-step:
-
Set up the problem: Write the dividend (11) inside the long division symbol and the divisor (4) outside.
4 | 11 -
Divide: How many times does 4 go into 11? It goes in 2 times (4 x 2 = 8). Write the 2 above the 11.
2 4 | 11 -
Multiply: Multiply the quotient (2) by the divisor (4): 2 x 4 = 8. Write this result below the 11.
2 4 | 11 8 -
Subtract: Subtract the result (8) from the dividend (11): 11 - 8 = 3. This is the remainder.
2 4 | 11 8 -- 3
Therefore, 11 ÷ 4 = 2 with a remainder of 3.
Method 2: Representing the Remainder as a Fraction
The remainder (3) can be expressed as a fraction of the divisor (4). This gives us a more complete representation of the division:
11 ÷ 4 = 2 and 3/4
This mixed number (2 and 3/4) represents the whole number quotient (2) and the fractional part of the division (3/4). This fractional representation is essential for many applications, especially those involving precise measurements or ratios.
Method 3: Converting to a Decimal
Instead of a mixed number, we can convert the remainder to a decimal. To do this, we extend the long division process:
-
Add a decimal point and a zero to the remainder:
2. 4 | 11.0 8 -- 30 -
Divide 30 by 4: 30 ÷ 4 = 7 with a remainder of 2. Write the 7 after the decimal point.
2.7 4 | 11.0 8 -- 30 28 -- 2 -
Continue adding zeros and dividing until you reach the desired level of precision or the remainder becomes zero. In this case, adding another zero results in 20 ÷ 4 = 5.
2.75 4 | 11.00 8 -- 30 28 -- 20 20 -- 0
Therefore, 11 ÷ 4 = 2.75
The Significance of Remainders and Fractions
The remainder in 11 ÷ 4 highlights the limitations of whole number division. Not all divisions result in a whole number quotient. The remainder represents the portion of the dividend that is left over after the divisor has been applied as many times as possible. Expressing this remainder as a fraction or decimal allows for a more precise representation of the result and enables us to work with fractional parts in subsequent calculations.
Real-World Applications
The concept of dividing 11 by 4, and understanding its remainder and fractional/decimal representation, is applied extensively in various fields:
-
Sharing: Imagine sharing 11 cookies among 4 friends. Each friend would get 2 cookies (the whole number quotient), and there would be 3 cookies left over (the remainder), which could be further divided and shared.
-
Measurement: Imagine cutting a ribbon of 11 inches into 4 equal pieces. Each piece would be 2.75 inches long. The decimal representation is crucial for accuracy in this context.
-
Ratio and Proportion: Understanding fractions helps in solving problems involving ratios and proportions. For example, if the ratio of boys to girls in a class is 4:3 and there are 11 students in total, determining the exact number of boys and girls requires understanding fractions and remainders.
-
Programming and Computing: Remainders (often obtained using the modulo operator, %) are fundamental in computer programming for tasks such as determining even or odd numbers, generating cyclical patterns, and handling data structures.
Expanding the Concept: Beyond Basic Division
The seemingly simple problem of 11 ÷ 4 opens the door to a broader understanding of mathematical concepts:
-
Rational Numbers: The result 2.75 is a rational number, a number that can be expressed as a fraction of two integers. Understanding rational numbers is crucial for advanced mathematical concepts.
-
Decimal Representation: The decimal representation of 2.75 highlights the relationship between fractions and decimals, showcasing different ways to represent the same value.
-
Approximation and Rounding: In some contexts, it might be necessary to round the result. For example, rounding 2.75 to the nearest whole number would give 3. Understanding when and how to round is important for practical applications.
-
Modulo Operator: The remainder in division (3 in this case) is often represented using the modulo operator (%) in programming. This operator returns the remainder after division, enabling various computational tasks.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 3/4?
A: The fraction 3/4 is already in its simplest form because 3 and 4 have no common factors other than 1.
Q: Can 11 ÷ 4 be expressed as a percentage?
A: Yes, 2.75 can be expressed as a percentage by multiplying by 100: 2.75 x 100 = 275%.
Q: What are some other methods to solve 11 ÷ 4?
A: While long division is the most common method, you could also use a calculator, or break the problem down into simpler divisions (e.g., dividing 8 by 4 and then dividing the remaining 3 by 4 separately).
Q: Is there a way to solve this without using long division?
A: While long division is the most efficient method for manual calculation, you could use estimation and mental math. You know 4 x 2 = 8, which is close to 11, leaving a remainder of 3. Then, you can express the remainder as a fraction or decimal.
Conclusion: A Deeper Appreciation for Division
This exploration of 11 ÷ 4 reveals that even the simplest arithmetic problems hold layers of mathematical richness. Understanding the quotient, remainder, and different ways to represent the result—as a mixed number or a decimal—is crucial for developing a comprehensive understanding of division and its practical applications in various fields. The concepts explored here extend beyond elementary arithmetic and form the foundation for more advanced mathematical concepts and problem-solving. The seemingly simple act of dividing 11 by 4 provides a powerful illustration of the elegance and utility of mathematical principles. It's a reminder that even the most basic mathematical operations can reveal surprising depths and complexities when examined closely.
Latest Posts
Latest Posts
-
66 6 Kg To Lbs
Sep 20, 2025
-
28 Mph To Km
Sep 20, 2025
-
456 Minutes In Hours
Sep 20, 2025
-
163 Pounds In Kilos
Sep 20, 2025
-
Who Ran Over Myrtle
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 11 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.