12 16 In Percentage
renascent
Sep 21, 2025 · 5 min read
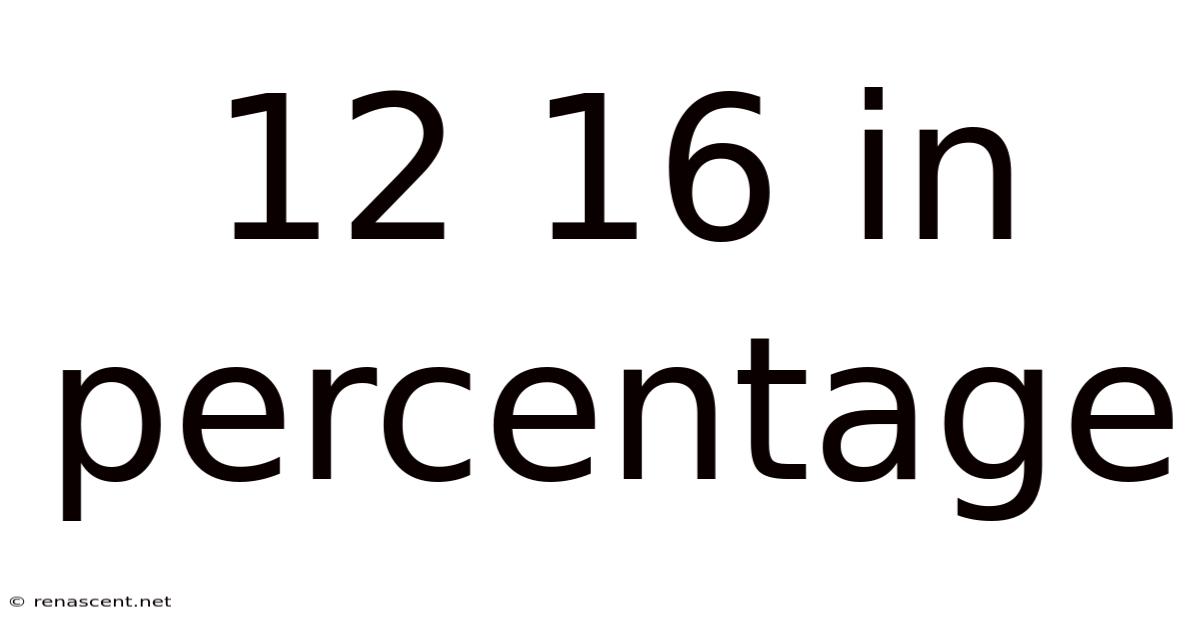
Table of Contents
Decoding 12/16 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in a shop to analyzing statistical data. This article delves into the process of converting the fraction 12/16 into a percentage, providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also examine the broader context of fraction-to-percentage conversions and their real-world relevance.
Introduction: Understanding Fractions and Percentages
Before we tackle the conversion of 12/16 to a percentage, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" is used to represent "per cent," meaning "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Step-by-Step Conversion of 12/16 to a Percentage
Converting 12/16 to a percentage involves a simple two-step process:
Step 1: Simplify the Fraction
The fraction 12/16 can be simplified by finding the greatest common divisor (GCD) of the numerator (12) and the denominator (16). The GCD of 12 and 16 is 4. Dividing both the numerator and the denominator by 4, we get:
12 ÷ 4 = 3 16 ÷ 4 = 4
Therefore, the simplified fraction is 3/4.
Step 2: Convert the Simplified Fraction to a Percentage
To convert the simplified fraction 3/4 to a percentage, we can use the following methods:
- Method 1: Using Division
Divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Now, multiply the decimal result by 100 to express it as a percentage:
0.75 × 100 = 75%
Therefore, 12/16 is equivalent to 75%.
- Method 2: Finding an Equivalent Fraction with a Denominator of 100
We can also convert 3/4 to a percentage by finding an equivalent fraction with a denominator of 100. To do this, we need to determine what number we must multiply the denominator (4) by to get 100. This number is 25 (100 ÷ 4 = 25). We must then multiply the numerator by the same number:
3 × 25 = 75 4 × 25 = 100
This gives us the equivalent fraction 75/100, which is equal to 75%.
The Mathematical Principles Behind the Conversion
The conversion from a fraction to a percentage relies on the fundamental concept of proportionality. A percentage represents a proportion out of 100. When we convert a fraction to a percentage, we are essentially finding the equivalent fraction with a denominator of 100. This process maintains the same ratio between the numerator and the denominator.
The division step in the conversion process reflects the act of finding the decimal representation of the fraction. Multiplying by 100 then scales this decimal representation to express it as a proportion of 100 – a percentage.
Real-World Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is crucial in numerous real-world scenarios. Here are just a few examples:
-
Calculating Discounts: Sales often advertise discounts as percentages. Understanding how to convert fractions to percentages helps you quickly determine the actual savings on an item. For instance, a 3/4 discount is equivalent to a 75% discount.
-
Analyzing Test Scores: Test scores are often represented as fractions (e.g., 12 out of 16 correct answers). Converting this fraction to a percentage provides a more readily understandable representation of performance.
-
Understanding Financial Data: Financial reports frequently use percentages to represent various aspects of a company's financial health, such as profit margins, growth rates, and debt ratios. Converting fractions to percentages helps in interpreting and comparing this data.
-
Interpreting Statistical Data: Statistics often involve analyzing data presented as fractions or ratios. Converting these to percentages makes the data easier to understand and compare.
-
Cooking and Baking: Many recipes use fractions to specify ingredient quantities. Understanding percentage equivalents can be helpful for adjusting recipes to different sizes or accommodating dietary restrictions.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
Yes, any fraction can be converted to a percentage using the methods described above.
Q2: What if the resulting percentage has a decimal?
Sometimes the result will have a decimal, such as 66.67%. This is perfectly acceptable. You may round the percentage to a convenient number of decimal places depending on the context.
Q3: What if the fraction is an improper fraction (numerator is larger than the denominator)?
An improper fraction will result in a percentage greater than 100%. For example, 16/12 would be converted to 133.33%. This indicates a value exceeding the whole.
Q4: Are there online calculators for fraction-to-percentage conversion?
Yes, many online calculators are available that can quickly convert fractions to percentages. However, understanding the underlying process is essential for building mathematical proficiency.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with far-reaching applications. The process, while straightforward, hinges on understanding the relationship between fractions and percentages, specifically the concept of proportionality and the equivalence of representing parts of a whole. By mastering this conversion, you equip yourself with a valuable tool for navigating various numerical situations in your academic, professional, and personal life. Remember the two core steps: simplify the fraction first, then convert the simplified fraction to a percentage using division and multiplication by 100, or by finding an equivalent fraction with a denominator of 100. The choice of method depends on personal preference and the specific context of the problem. This comprehensive guide provides a strong foundation for tackling similar conversion problems in the future. Practice makes perfect – the more you work with fractions and percentages, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
1 4 Of 20
Sep 21, 2025
-
80 5 Kg In Pounds
Sep 21, 2025
-
166 Min To Hours
Sep 21, 2025
-
Rudy In Ice Age
Sep 21, 2025
-
150 Gm To Oz
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 12 16 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.