12 X 4 2
renascent
Sep 24, 2025 · 5 min read
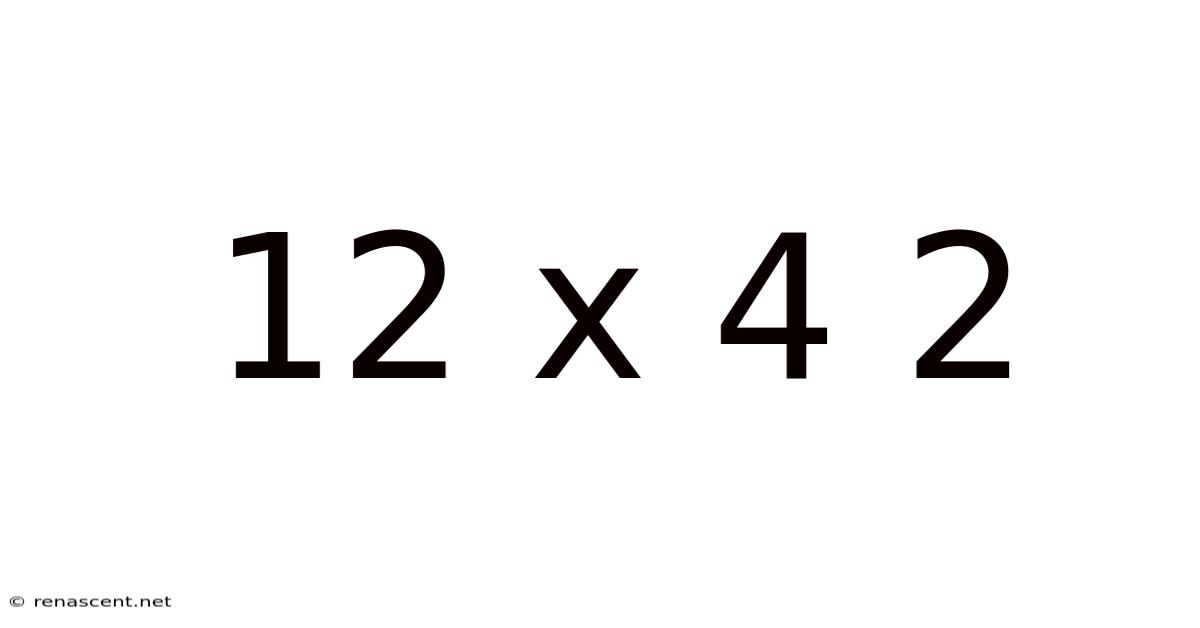
Table of Contents
Decoding 12 x 4 ÷ 2: A Deep Dive into Order of Operations and Mathematical Precision
The seemingly simple equation "12 x 4 ÷ 2" often sparks debate, highlighting the crucial importance of understanding the order of operations in mathematics. This article will not only solve this equation but delve into the underlying principles, exploring different approaches and addressing common misconceptions. We'll cover the fundamental rules, explain the significance of mathematical precision, and ultimately equip you with a solid understanding of how to tackle similar problems confidently.
Introduction: The Order of Operations – PEMDAS/BODMAS
The core principle governing the solution of this equation, and indeed many others involving multiple operations, is the order of operations. This is often remembered using mnemonics such as PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both mnemonics represent the same fundamental hierarchy. The key takeaway is that multiplication and division hold equal precedence, as do addition and subtraction. When faced with operations of equal precedence, we proceed from left to right.
Step-by-Step Solution: Applying PEMDAS/BODMAS
Let's apply the order of operations to solve "12 x 4 ÷ 2":
-
Multiplication and Division (from left to right): Following PEMDAS/BODMAS, we perform multiplication and division before addition and subtraction. Crucially, multiplication and division have equal precedence, so we work from left to right.
-
First Operation: 12 x 4 = 48: We begin with the multiplication on the left side of the equation.
-
Second Operation: 48 ÷ 2 = 24: Next, we perform the division.
-
Final Result: 24: The final answer to the equation "12 x 4 ÷ 2" is 24.
Illustrative Examples: Highlighting the Importance of Order
To further underscore the significance of the order of operations, let's consider alternative arrangements of the same numbers and operations:
-
Example 1: (12 x 4) ÷ 2: Using parentheses alters the order. We first calculate 12 x 4 = 48, then divide by 2 to get 24. This emphasizes that parentheses force a specific order of calculation.
-
Example 2: 12 x (4 ÷ 2): Here, the parentheses change the calculation again. We start with 4 ÷ 2 = 2, then multiply by 12, resulting in 24. Note that even with parenthesis, the final answer remains the same as it follows the correct order of operations.
-
Example 3: Incorrect Order: If we were to incorrectly perform the division before the multiplication (2 ÷ 4 x 12), the answer would be drastically different. 0.5 x 12 equals 6, a completely erroneous result compared to the correct answer of 24. This exemplifies the need to strictly adhere to PEMDAS/BODMAS.
Beyond the Basics: Exploring More Complex Equations
The principles illustrated with "12 x 4 ÷ 2" are fundamental to solving far more complex mathematical expressions. Consider an equation like:
3 + 5 x (2 + 3) – 4 ÷ 2
-
Parentheses/Brackets: First, we solve the expression within the parentheses: (2 + 3) = 5.
-
Multiplication and Division (left to right): Next, we perform multiplication and division from left to right: 5 x 5 = 25 and 4 ÷ 2 = 2.
-
Addition and Subtraction (left to right): Finally, we carry out addition and subtraction from left to right: 3 + 25 – 2 = 26.
The Significance of Mathematical Precision:
The accuracy of mathematical calculations is paramount across numerous fields. From engineering and finance to scientific research and software development, errors in calculation can have significant consequences. The correct application of the order of operations is essential for ensuring accuracy and reliability. A small mistake in the order of operations in a large calculation could lead to an entirely incorrect result, potentially with severe ramifications.
Common Misconceptions and Errors:
Many mistakes stem from misunderstanding the equal precedence of multiplication and division (or addition and subtraction). People sometimes prioritize multiplication over division, or vice-versa, without considering the left-to-right rule. This is where a clear understanding of PEMDAS/BODMAS becomes crucial. Another common error involves neglecting the parentheses or brackets and incorrectly performing operations in the order they appear in the equation.
Frequently Asked Questions (FAQ):
-
Q: Why is the order of operations important?
- A: The order of operations ensures consistent and accurate results when solving mathematical expressions with multiple operations. Without a set order, the result would vary based on individual interpretation.
-
Q: What happens if there are multiple sets of parentheses?
- A: In the case of nested parentheses, you begin with the innermost set and work your way outwards.
-
Q: Does the order of operations apply to all mathematical operations?
- A: Yes, the order of operations applies to all standard mathematical operations including addition, subtraction, multiplication, division, exponents, and roots. Special functions or operations might have their own precedence rules, which should be specified.
-
Q: Are there any exceptions to PEMDAS/BODMAS?
- A: While PEMDAS/BODMAS is generally accepted, the key is to always pay attention to the explicit instructions given within the problem. Parentheses or brackets can significantly alter the order.
-
Q: How can I improve my understanding of order of operations?
- A: Practice is key! Work through many example problems, varying the complexity. Using online resources, textbooks, or educational apps can also help reinforce your understanding.
Conclusion: Mastering the Fundamentals
Understanding the order of operations is not merely about solving simple equations like "12 x 4 ÷ 2"; it's about acquiring a fundamental skill crucial for mathematical proficiency. This seemingly basic principle underpins more complex calculations across various disciplines. By grasping the principles of PEMDAS/BODMAS and adhering to them meticulously, you can ensure accuracy, avoid common pitfalls, and build a stronger foundation in mathematics. Remember the simple steps, practice consistently, and you will confidently navigate even the most complex mathematical expressions. The ability to perform calculations accurately and efficiently is a valuable skill that will serve you well in many aspects of life and learning.
Latest Posts
Latest Posts
-
Can Dogs Eat Skittles
Sep 24, 2025
-
4pi 3 To Degrees
Sep 24, 2025
-
Plancks Constant In Ev
Sep 24, 2025
-
Define Lower Explosive Limit
Sep 24, 2025
-
Life Expectancy For Niger
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 12 X 4 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.