13 25 As Percent
renascent
Sep 22, 2025 · 5 min read
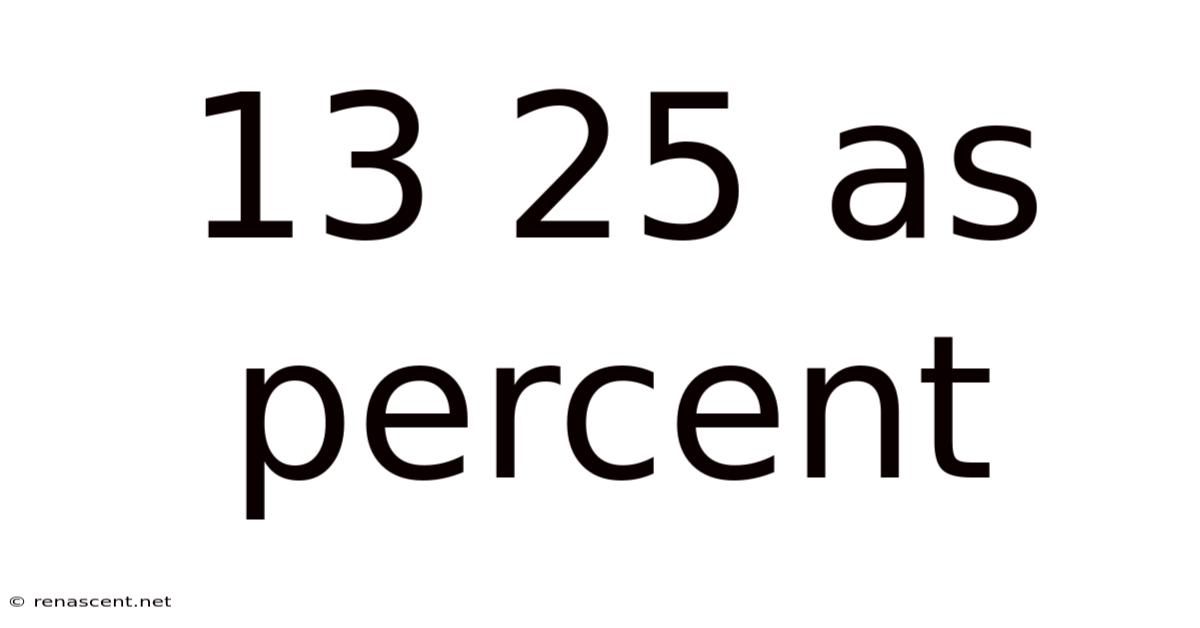
Table of Contents
13/25 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable in numerous everyday situations, from calculating discounts and taxes to understanding statistics and financial reports. This comprehensive guide will delve into the specifics of calculating 13/25 as a percentage, explaining the process step-by-step and exploring related concepts. We will also address common misconceptions and provide you with the tools to confidently tackle similar percentage problems. By the end, you'll not only know the answer but also understand the underlying principles, empowering you to solve a wide range of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin words "per centum," meaning "out of a hundred." Therefore, 1% represents 1/100, 50% represents 50/100 (or 1/2), and 100% represents 100/100 (or the whole).
Percentages are incredibly useful for comparing and understanding proportions. They provide a standardized way to express parts of a whole, making comparisons easier regardless of the size of the whole. For instance, comparing a 10% increase in sales for a small business to a 10% increase in sales for a multinational corporation is easily understood because the percentage provides a relative measure of the increase.
Calculating 13/25 as a Percentage: Step-by-Step
To convert the fraction 13/25 into a percentage, we need to express it as a fraction with a denominator of 100. Here's how:
Step 1: Convert the fraction to a decimal.
Divide the numerator (13) by the denominator (25):
13 ÷ 25 = 0.52
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.52 x 100 = 52%
Therefore, 13/25 is equal to 52%.
Alternative Method: Using Proportions
Another approach to solve this problem involves setting up a proportion:
13/25 = x/100
To solve for 'x' (the percentage), we can cross-multiply:
25x = 1300
Now, divide both sides by 25:
x = 1300 ÷ 25 = 52
Therefore, x = 52%, confirming our previous result. This method highlights the relationship between fractions and percentages more explicitly.
Understanding the Relationship Between Fractions, Decimals, and Percentages
These three representations are interconnected and easily convertible. Understanding their relationships is key to mastering percentage calculations:
- Fraction to Decimal: Divide the numerator by the denominator.
- Decimal to Percentage: Multiply the decimal by 100 and add the % symbol.
- Percentage to Decimal: Divide the percentage by 100.
- Decimal to Fraction: Express the decimal as a fraction with a denominator of a power of 10 (e.g., 0.52 can be expressed as 52/100).
- Percentage to Fraction: Divide the percentage by 100 and simplify the fraction.
- Fraction to Percentage: Convert the fraction to a decimal, then multiply by 100 and add the % symbol.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages has a wide range of applications in real-world scenarios:
- Discounts: A store offering a 20% discount on a $50 item requires calculating 20% of $50.
- Taxes: Determining the amount of sales tax or income tax payable involves percentage calculations.
- Interest Rates: Calculating simple or compound interest on loans or investments relies heavily on percentages.
- Grade Calculations: Converting scores on tests or assignments into percentages provides a standardized way to evaluate performance.
- Data Analysis: Interpreting statistical data often involves understanding and comparing percentages.
- Financial Reporting: Financial statements use percentages extensively to express ratios, growth rates, and profitability.
- Tip Calculation: Calculating a gratuity in a restaurant involves determining a percentage of the total bill.
Common Mistakes to Avoid
Several common mistakes can arise when calculating percentages:
- Incorrect Order of Operations: Remember to follow the correct order of operations (PEMDAS/BODMAS) when solving more complex problems involving percentages.
- Misunderstanding of Percentage Points: A change from 10% to 15% is a 5 percentage point increase, not a 5% increase. A 5% increase would be from 10% to 10.5%.
- Confusing Percentages and Decimals: Make sure to convert decimals to percentages correctly by multiplying by 100.
- Rounding Errors: Be mindful of rounding errors, especially in financial calculations where accuracy is crucial.
Advanced Percentage Calculations
While calculating 13/25 as a percentage is a straightforward example, more complex percentage problems may involve:
- Finding the percentage increase or decrease: (New Value - Old Value) / Old Value * 100%
- Calculating a percentage of a percentage: Multiply the percentages as decimals.
- Determining the original value after a percentage change: This often involves using algebra to solve for the unknown variable.
Frequently Asked Questions (FAQs)
Q: How do I calculate a percentage of a number?
A: To calculate a percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, 20% of 50 is 50 * 0.20 = 10.
Q: What is the difference between a percentage and a percentage point?
A: A percentage represents a proportion of a whole, while a percentage point represents the absolute difference between two percentages.
Q: How can I improve my understanding of percentages?
A: Practice regularly by solving various percentage problems, use online calculators and tutorials, and focus on understanding the underlying concepts.
Conclusion
Converting 13/25 to a percentage is a simple yet fundamental calculation with far-reaching applications. By understanding the steps involved, the relationship between fractions, decimals, and percentages, and avoiding common pitfalls, you can confidently tackle a wide range of percentage-related problems. This knowledge will prove invaluable in various aspects of your personal and professional life, empowering you to make informed decisions and effectively analyze data. Remember, consistent practice is key to mastering this important mathematical skill. Through practice and a clear understanding of the underlying principles, you can become proficient in tackling even more complex percentage calculations.
Latest Posts
Latest Posts
-
19 0 Celsius To Fahrenheit
Sep 22, 2025
-
3 Divided By 56
Sep 22, 2025
-
3 4 Of A Tsp
Sep 22, 2025
-
1000 Divided By 8
Sep 22, 2025
-
31 35 As A Percentage
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 13 25 As Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.