1300 Divided By 3
renascent
Sep 14, 2025 · 6 min read
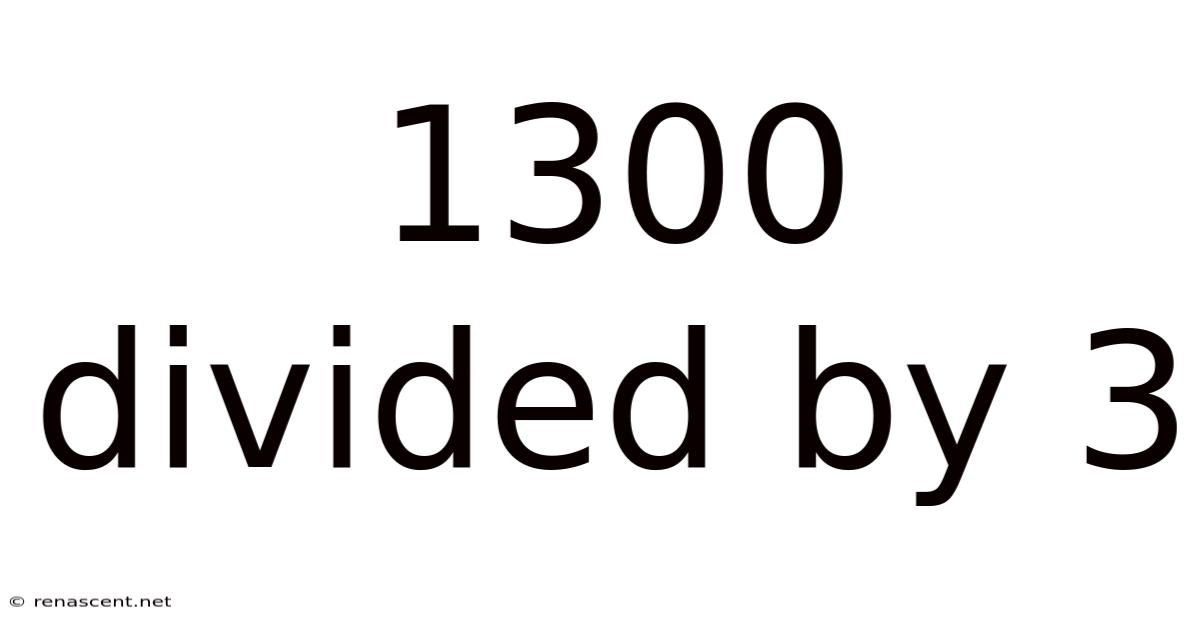
Table of Contents
Diving Deep into Division: Unveiling the Answer to 1300 Divided by 3
This article explores the seemingly simple problem of dividing 1300 by 3, delving far beyond the basic answer. We'll examine various methods for solving this problem, understand the underlying mathematical concepts, explore practical applications, and address common misconceptions. This comprehensive guide is perfect for anyone looking to improve their understanding of division, from elementary school students to adults refreshing their math skills. We'll uncover the beauty and logic behind this fundamental arithmetic operation.
I. Introduction: The Basics of Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. When we say "1300 divided by 3," we're asking: "How many times does 3 fit into 1300?" The answer to this question reveals the quotient, while any remaining amount is called the remainder. Understanding this foundational concept is key to mastering division.
II. Methods for Solving 1300 Divided by 3
Several methods exist to solve 1300 ÷ 3. Let's explore a few:
-
Long Division: This classic method is a systematic approach perfect for understanding the process.
-
Set up the problem: 3 | 1300
-
Divide the first digit (1) by 3. It doesn't go, so we move to the next digit.
-
Divide 13 by 3. 3 goes into 13 four times (3 x 4 = 12), with a remainder of 1. Write the 4 above the 3 in 1300.
-
Bring down the next digit (0). The remainder 1 becomes 10.
-
Divide 10 by 3. 3 goes into 10 three times (3 x 3 = 9), with a remainder of 1. Write the 3 above the 0 in 1300.
-
Bring down the next digit (0). The remainder 1 becomes 10.
-
Divide 10 by 3. 3 goes into 10 three times (3 x 3 = 9), with a remainder of 1. Write the 3 above the 0.
-
The final remainder is 1.
Therefore, 1300 ÷ 3 = 433 with a remainder of 1.
-
-
Repeated Subtraction: This method involves repeatedly subtracting 3 from 1300 until you reach 0 or a number less than 3. While effective for smaller numbers, it becomes tedious for larger numbers like 1300.
-
Using a Calculator: The simplest method, especially for larger numbers, is to use a calculator. Inputting "1300 ÷ 3" will instantly provide the answer: 433.333... This illustrates that the division results in a decimal answer.
III. Understanding the Result: Quotient and Remainder
As we discovered using long division, 1300 divided by 3 yields a quotient of 433 and a remainder of 1.
-
Quotient: This represents the number of times 3 divides evenly into 1300. In this case, it's 433.
-
Remainder: This is the amount left over after the even division. Here, the remainder is 1. This signifies that 1300 is not perfectly divisible by 3.
IV. Decimal Representation: Exploring the Remainder
The calculator's answer (433.333...) reveals a decimal representation. This decimal portion represents the remainder expressed as a fraction of the divisor (3). The repeating decimal .333... is equivalent to the fraction 1/3. Therefore, 433.333... can be written as 433 + 1/3, which is equivalent to the result obtained through long division: 433 with a remainder of 1.
V. Practical Applications: Real-World Examples
Division problems like 1300 ÷ 3 appear frequently in various real-world scenarios:
-
Sharing Equally: Imagine you have 1300 candies to distribute equally among 3 friends. Each friend would receive 433 candies, and you'd have 1 candy left over.
-
Averaging: If you've collected 1300 data points and need to find the average over 3 periods, dividing 1300 by 3 helps calculate the average per period.
-
Measurement Conversions: Many unit conversions involve division. For example, converting 1300 centimeters into meters (1 meter = 100 centimeters) would involve dividing 1300 by 100.
-
Resource Allocation: Businesses often use division to allocate resources fairly among different departments or projects.
VI. Expanding Understanding: Exploring Divisibility Rules
Understanding divisibility rules can help predict whether a number is evenly divisible by another without performing the actual division. A number is divisible by 3 if the sum of its digits is divisible by 3. Let's check 1300:
1 + 3 + 0 + 0 = 4
Since 4 is not divisible by 3, we know 1300 is not perfectly divisible by 3. This confirms our earlier findings.
VII. Beyond the Basics: Prime Factorization and Factors
Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). The prime factorization of 1300 is 2² x 5² x 13. This representation offers deeper insights into the number's properties. Similarly, understanding the factors of 1300 (the numbers that divide evenly into 1300) provides further understanding.
VIII. Connecting Division to Other Operations: Inverse Relationships
Division has an inverse relationship with multiplication. If 1300 ÷ 3 = 433 R 1, then 3 x 433 + 1 = 1300. This demonstrates the fundamental link between these two operations. Mastering one strengthens your understanding of the other.
IX. Addressing Common Misconceptions
-
Ignoring Remainders: Many students make the mistake of neglecting the remainder. The remainder is a crucial part of the division process and holds significant meaning in various applications.
-
Confusing Quotient and Remainder: Clearly distinguishing between the quotient (the result of the division) and the remainder (the leftover amount) is essential for accurate interpretation.
-
Approximations: While using a calculator might offer a decimal approximation, understanding the whole number quotient and the remainder provides a more precise and complete solution in many situations.
X. Further Exploration: Advanced Division Concepts
-
Modular Arithmetic: This branch of number theory focuses on remainders after division. In modular arithmetic, 1300 modulo 3 (written as 1300 mod 3) would be 1, indicating the remainder when 1300 is divided by 3.
-
Division with Negative Numbers: Extending division to include negative numbers introduces additional considerations regarding signs.
-
Division of Polynomials: This is an advanced topic involving dividing expressions containing variables.
XI. Frequently Asked Questions (FAQs)
-
Q: Can I express the answer as a decimal? A: Yes, 1300 ÷ 3 = 433.333... (a repeating decimal).
-
Q: What does the remainder represent? A: The remainder (1 in this case) represents the amount left over after dividing 1300 into equal groups of 3.
-
Q: What are some real-world applications beyond the examples given? A: Many situations in finance, engineering, and everyday life involve dividing quantities into equal parts or determining averages.
XII. Conclusion: The Power of Understanding Division
Mastering division is not just about finding an answer; it's about understanding the fundamental principles behind sharing, distributing, and averaging quantities. Through long division, repeated subtraction, and using calculators, we've explored various approaches to solving 1300 ÷ 3, understanding the significance of both the quotient and the remainder. The ability to perform and interpret division accurately is a critical skill applicable across numerous disciplines and everyday situations. By grasping the concepts outlined in this article, you can move beyond simply calculating the answer and develop a deeper, more intuitive understanding of this core arithmetic operation. Keep practicing, exploring, and never stop questioning—that's the key to unlocking the power of mathematics!
Latest Posts
Latest Posts
-
12590 Divided By 7
Sep 15, 2025
-
6 Oz To Tbsp
Sep 15, 2025
-
Great War For Civilization
Sep 15, 2025
-
150 Km To Miles
Sep 15, 2025
-
1 8 In Fraction Form
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1300 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.