15 Divided By 10
renascent
Sep 19, 2025 · 5 min read
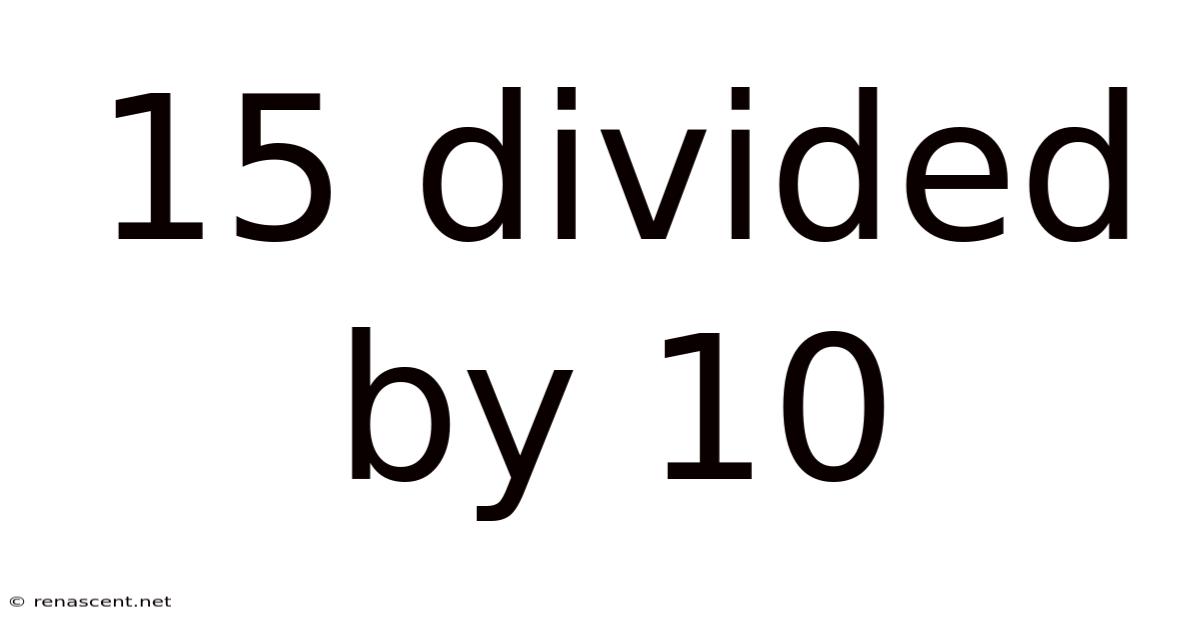
Table of Contents
15 Divided by 10: A Deep Dive into Division and Decimal Understanding
Introduction: This article explores the seemingly simple calculation of 15 divided by 10 (15 ÷ 10). While the answer might seem obvious at first glance – 1.5 – the process unveils fundamental concepts in mathematics, particularly division and the significance of decimal numbers. We'll delve into the mechanics of division, explore different methods for solving this problem, and discuss its practical applications and relevance in various contexts. Understanding this basic division problem provides a solid foundation for tackling more complex mathematical challenges.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. In the equation 15 ÷ 10, we are asking: "How many times does 10 fit into 15?". The number 15 is called the dividend (the number being divided), 10 is the divisor (the number by which we are dividing), and the result, 1.5, is the quotient.
The process of division can be visualized in several ways:
-
Sharing: Imagine you have 15 cookies and you want to share them equally among 10 friends. Each friend would receive 1.5 cookies.
-
Grouping: Consider arranging 15 objects into groups of 10. You would have one complete group of 10, and 5 objects remaining. This remainder represents the fractional part of the quotient.
Methods for Solving 15 ÷ 10
Several methods can be used to calculate 15 divided by 10:
1. Long Division:
Long division is a standard algorithm used to perform division manually. While seemingly cumbersome for this simple problem, it's crucial for understanding the process and applying it to more complex divisions.
1.5
10 | 15.0
-10
50
-50
0
This demonstrates that 10 goes into 15 once (1), leaving a remainder of 5. We add a decimal point and a zero to the dividend, effectively making it 15.0. Then, 10 goes into 50 five times (0.5), resulting in a quotient of 1.5.
2. Fraction Conversion:
Division can also be represented as a fraction. 15 ÷ 10 is equivalent to the fraction 15/10. This fraction can then be simplified:
15/10 = (5 x 3) / (5 x 2) = 3/2
This improper fraction (numerator larger than denominator) can be converted to a mixed number or decimal:
3/2 = 1 ½ = 1.5
3. Decimal Conversion:
Dividing by 10 is a particularly straightforward operation when working with decimals. Dividing a number by 10 simply moves the decimal point one place to the left. Since 15 is equivalent to 15.0, moving the decimal point one place to the left yields 1.5. This is a valuable shortcut to remember for quick calculations involving powers of 10.
Understanding the Decimal Result: 1.5
The result of 15 ÷ 10, 1.5, is a decimal number. Decimal numbers represent values between whole numbers using a decimal point. In 1.5, the '1' represents one whole unit, and the '.5' represents five-tenths (5/10) of a unit. Understanding decimal representation is crucial for many aspects of mathematics and everyday life.
Practical Applications of 15 ÷ 10
The calculation 15 ÷ 10, seemingly simple, has various practical applications across numerous fields:
-
Finance: Calculating discounts, splitting bills, or determining percentages often involves division. For example, a 10% discount on a $15 item would be calculated as 15 x 0.1 = $1.50.
-
Measurement: Converting units of measurement frequently requires division. For example, converting 15 centimeters to decimeters (1 decimeter = 10 centimeters) would involve dividing 15 by 10, resulting in 1.5 decimeters.
-
Data Analysis: Calculating averages, proportions, and ratios often uses division. For instance, if 15 out of 100 students passed an exam, the pass rate is 15 ÷ 100 = 0.15 or 15%.
-
Cooking and Baking: Dividing ingredients or adjusting recipes often involves fractions and decimals, based on the principles of division.
Extending the Concept: Division by Powers of 10
Understanding the division by 10 provides a springboard to grasp division by other powers of 10 (100, 1000, etc.). The pattern involves moving the decimal point to the left by the number of zeros in the divisor.
- 15 ÷ 100 = 0.15 (decimal point moves two places to the left)
- 15 ÷ 1000 = 0.015 (decimal point moves three places to the left)
Advanced Considerations: Remainders and Fractional Parts
While 15 ÷ 10 results in a clean decimal, many divisions result in remainders. Understanding how to handle remainders is crucial for comprehending division more comprehensively. Remainders can be expressed as fractions or decimals, depending on the context.
For instance, 17 ÷ 10 would leave a remainder of 7. This can be expressed as:
- Mixed Number: 1 ⁷⁄₁₀
- Decimal: 1.7
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 15/10?
A: The simplest form is 3/2. This is obtained by dividing both the numerator (15) and denominator (10) by their greatest common divisor, which is 5.
Q: Can 15 ÷ 10 be expressed as a percentage?
A: Yes, 15 ÷ 10 = 1.5, which is equivalent to 150%. This indicates that 15 is 150% of 10.
Q: What if I have to divide a number larger than 15 by 10?
A: The same principles apply. For example, 25 ÷ 10 = 2.5. The decimal point simply moves one place to the left.
Q: Why is understanding division by 10 important?
A: Division by 10 is fundamental for comprehending decimal numbers, percentages, and various real-world applications involving proportional reasoning and unit conversions.
Conclusion
The seemingly simple calculation of 15 divided by 10 provides a gateway to understanding fundamental mathematical concepts, including division, decimal numbers, fractions, and their practical applications. Mastering this basic operation lays a strong foundation for tackling more complex mathematical problems and builds a crucial skillset applicable in various aspects of life. From financial calculations to scientific measurements, the ability to perform and understand division is an invaluable asset. By exploring different methods of solving this problem and understanding the underlying principles, we gain a deeper appreciation for the power and versatility of mathematics. Remember that even simple calculations hold a wealth of knowledge and application, making the exploration of seemingly basic arithmetic incredibly rewarding.
Latest Posts
Latest Posts
-
136 Pounds To Kilograms
Sep 19, 2025
-
245 Lbs In Kilos
Sep 19, 2025
-
270 Kilometers To Miles
Sep 19, 2025
-
Convert Kpa To Mmhg
Sep 19, 2025
-
Stakeholder Power Interest Grid
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 15 Divided By 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.