15 Divided By 20
renascent
Sep 16, 2025 · 5 min read
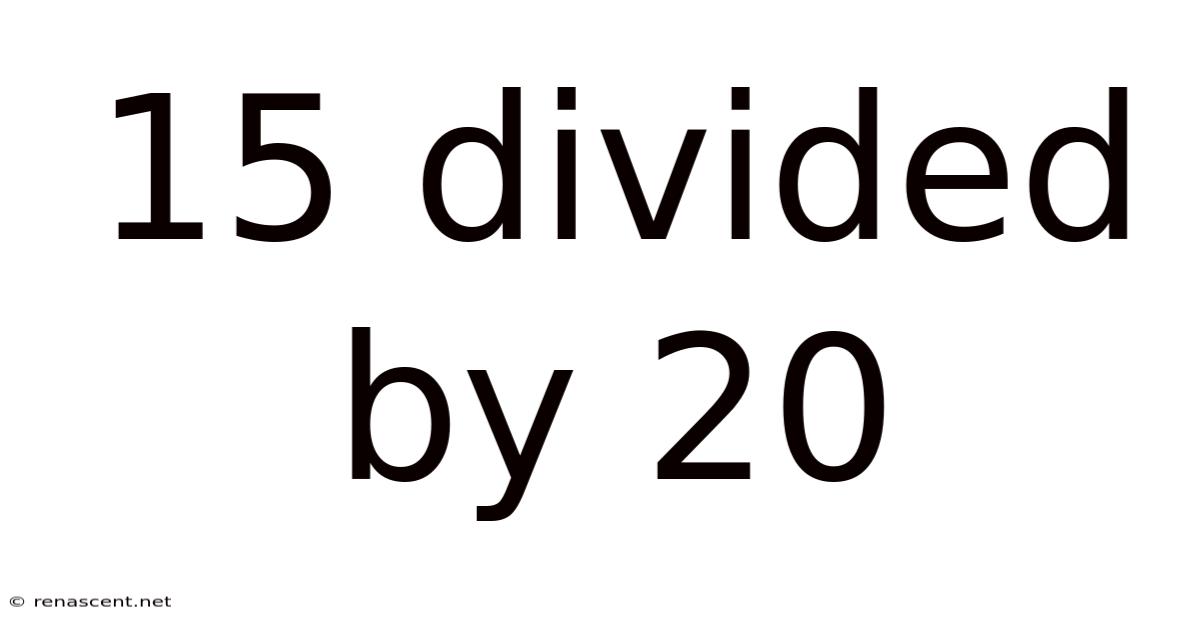
Table of Contents
Unpacking 15 Divided by 20: A Deep Dive into Division and Fractions
Dividing 15 by 20 might seem like a simple arithmetic problem, but it's a gateway to understanding fundamental mathematical concepts like fractions, decimals, percentages, and even ratios. This article will explore the different ways to solve this problem, delve into the underlying mathematical principles, and illustrate its practical applications. We'll move beyond a simple answer and uncover the rich tapestry of mathematical understanding woven into this seemingly straightforward calculation.
Understanding the Problem: 15 ÷ 20
The problem, 15 divided by 20 (15 ÷ 20), asks us to determine how many times 20 goes into 15. Since 20 is larger than 15, the answer will be less than 1. This immediately tells us that the result will be a fraction or a decimal less than one. This seemingly simple problem provides a fertile ground for exploring several important mathematical ideas.
Method 1: Direct Fraction Conversion
The most straightforward way to solve 15 ÷ 20 is to express it as a fraction: 15/20. This fraction represents 15 parts out of a total of 20 parts. The next step is to simplify this fraction by finding the greatest common divisor (GCD) of 15 and 20. The GCD is 5. Dividing both the numerator (15) and the denominator (20) by 5 gives us the simplified fraction:
15 ÷ 5 / 20 ÷ 5 = 3/4
Therefore, 15 divided by 20 is equal to 3/4. This is the simplest and most accurate representation of the answer.
Method 2: Decimal Conversion
While the fraction 3/4 is perfectly acceptable, it's often useful to express the answer as a decimal. To convert the fraction 3/4 to a decimal, we simply divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
So, 15 divided by 20 is equal to 0.75. This decimal representation is particularly useful when dealing with monetary values, measurements, or data analysis where decimal precision is required.
Method 3: Percentage Conversion
Percentages provide another useful way to represent the answer. To express 3/4 as a percentage, we multiply the fraction by 100%:
(3/4) * 100% = 75%
Therefore, 15 divided by 20 is equal to 75%. This representation is ideal when expressing proportions or comparing parts to a whole. For example, if you answered 15 out of 20 questions correctly on a test, you achieved a score of 75%.
The Concept of Ratios
The problem 15 ÷ 20 can also be interpreted as a ratio. A ratio is a comparison of two quantities. In this case, the ratio is 15:20, which simplifies to 3:4. This means that for every 3 units of one quantity, there are 4 units of another. Ratios are extensively used in various fields, including cooking (e.g., mixing ingredients), scaling models, and understanding proportions in various contexts.
Visual Representation: Understanding Fractions
A helpful way to visualize the fraction 3/4 is to imagine a pizza cut into 20 equal slices. If you eat 15 of these slices, you've consumed 15/20, or 3/4, of the pizza. This visual representation makes the concept of fractions more intuitive and easier to grasp. You can also use diagrams of bars, circles, or other shapes to represent the fraction visually, further enhancing understanding.
Long Division: A Step-by-Step Approach
While the previous methods are quicker for this specific problem, understanding long division is crucial for more complex division problems. Let’s perform long division for 15 ÷ 20:
- Set up the division: 20)15
- Add a decimal point and a zero: 20)15.0
- Divide: 20 does not go into 15, so we put a 0 before the decimal point. Now we divide 20 into 150. 20 goes into 150 seven times (20 x 7 = 140).
- Subtract: 150 - 140 = 10
- Add another zero: 20)15.00
- Divide: 20 goes into 100 five times (20 x 5 = 100).
- Subtract: 100 - 100 = 0
Therefore, the result of the long division is 0.75. This method demonstrates the process clearly, making it suitable for explaining division concepts to learners.
Practical Applications of 15/20 (0.75 or 75%)
The result of 15 divided by 20, expressed in various forms, has numerous real-world applications:
- Test Scores: As mentioned earlier, a score of 15 out of 20 translates to 75%.
- Sales and Discounts: A 75% discount means you pay only 25% of the original price.
- Cooking and Baking: Recipes often use ratios for ingredients.
- Measurements: Converting units of measurement might involve division and fractions.
- Data Analysis: Percentages are crucial in representing data proportions.
- Financial Calculations: Understanding percentages is fundamental for interest calculations, discounts, and profit margins.
Frequently Asked Questions (FAQ)
-
Can I express the answer as a mixed number? No, since the numerator (15) is smaller than the denominator (20), the result is a proper fraction, and a mixed number is not applicable in this case.
-
What if the numbers were larger? The same principles apply. You would simplify the fraction, convert to a decimal, or use long division.
-
Is there a calculator for this? Yes, any basic calculator can perform this division.
-
Why is simplifying fractions important? Simplifying fractions makes them easier to understand and compare. It provides the most concise representation of the ratio.
-
Why are different representations (fraction, decimal, percentage) useful? Different representations are useful depending on the context. Fractions are precise and easily visualized. Decimals are practical for calculations and measurements. Percentages are best for comparisons and proportions.
Conclusion: Beyond the Simple Answer
While the answer to 15 divided by 20 is seemingly simple (3/4, 0.75, or 75%), this problem offers a valuable opportunity to explore several key mathematical concepts. Understanding fractions, decimals, percentages, ratios, and long division are fundamental skills applicable across various disciplines and everyday situations. By breaking down this simple problem, we've gained a deeper appreciation for the interconnectedness of mathematical ideas and their practical relevance in our lives. This comprehensive exploration moves beyond a mere numerical answer, fostering a more robust and intuitive understanding of core mathematical principles.
Latest Posts
Latest Posts
-
39 Inches To Feet
Sep 16, 2025
-
9 12 As Percent
Sep 16, 2025
-
128 Millimeters To Inches
Sep 16, 2025
-
169 Pounds To Kilograms
Sep 16, 2025
-
Ecg Lead 3 Placement
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 15 Divided By 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.