15 Percent Of 25
renascent
Sep 14, 2025 · 6 min read
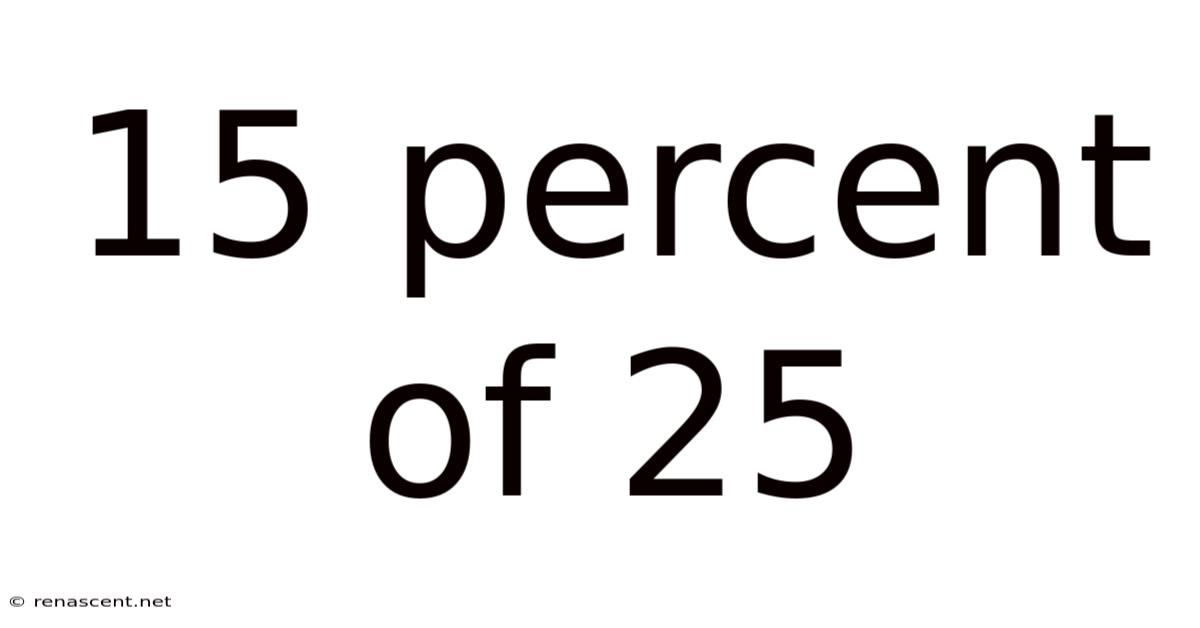
Table of Contents
Decoding 15 Percent of 25: A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article explores the seemingly simple calculation of "15 percent of 25," delving far beyond the immediate answer to illuminate the underlying concepts and practical applications of percentage calculations. Understanding percentages empowers you to make informed decisions, interpret data critically, and navigate the numerical world with confidence. This comprehensive guide will not only show you how to calculate 15% of 25 but will also equip you with the knowledge and tools to tackle any percentage problem with ease.
Understanding Percentages: The Basics
Before we dive into the specifics of calculating 15% of 25, let's solidify our understanding of percentages themselves. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 15% can be written as the fraction 15/100 or the decimal 0.15. This representation is crucial for performing percentage calculations effectively.
Method 1: Converting to Decimal
The most straightforward method for calculating 15% of 25 involves converting the percentage to its decimal equivalent. As mentioned above, 15% is equal to 0.15. To find 15% of 25, we simply multiply 25 by 0.15:
25 * 0.15 = 3.75
Therefore, 15% of 25 is 3.75.
Method 2: Using Fractions
Alternatively, we can use the fractional representation of 15%, which is 15/100. To find 15% of 25, we multiply 25 by 15/100:
25 * (15/100) = (25 * 15) / 100 = 375 / 100 = 3.75
This method reinforces the understanding that percentages are essentially fractions. Simplifying the fraction before multiplication can sometimes make the calculation easier, especially with larger numbers.
Method 3: Proportion Method
The proportion method offers a more visual and intuitive approach to solving percentage problems. We can set up a proportion to solve for the unknown value (x), which represents 15% of 25:
15/100 = x/25
To solve for x, we cross-multiply:
15 * 25 = 100 * x
375 = 100x
x = 375/100 = 3.75
This method highlights the relationship between the percentage, the whole value, and the part we are trying to find. It's particularly useful for understanding the underlying logic of percentage calculations.
Practical Applications: Where Percentages Matter
The ability to calculate percentages is a highly valuable skill with wide-ranging applications:
-
Finance and Budgeting: Calculating interest rates, discounts, taxes, tips, and investment returns all rely heavily on percentage calculations. Understanding these calculations is crucial for managing personal finances effectively. For example, calculating sales tax on a purchase, determining the discount on a sale item, or calculating the interest earned on a savings account all involve percentage calculations.
-
Retail and Sales: Businesses use percentages to determine markups, discounts, and profit margins. Analyzing sales data and forecasting future performance also requires a solid understanding of percentages. Calculating the percentage increase or decrease in sales from one period to another provides valuable insights into business trends and helps guide strategic decision-making.
-
Science and Statistics: Percentages are frequently used to express probabilities, error margins, and statistical significance in scientific research and data analysis. For instance, reporting the percentage of participants in a study who experienced a certain outcome or calculating the margin of error in a survey are common uses of percentages in scientific contexts.
-
Everyday Life: From calculating the percentage of a tip at a restaurant to determining the nutritional value of food products (e.g., percentage of daily value), percentages are integral to our daily lives. Understanding percentage change allows us to compare values over time, such as tracking progress on a fitness goal or analyzing changes in the price of goods.
-
Education: Understanding percentages is essential for students to analyze their academic performance (e.g., calculating their percentage grade), interpret data in various subjects, and even prepare for standardized tests. Many standardized tests include questions related to percentage calculations and their applications in various scenarios.
Beyond the Basics: More Complex Percentage Problems
While calculating 15% of 25 is relatively straightforward, the principles involved extend to more complex scenarios:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to determine what percentage one number is of another. For example, what percentage is 5 of 20? (Answer: 25%)
-
Finding the Original Value: You might know the percentage and the resulting value, but need to find the original number. For example, if 20% of a number is 10, what is the original number? (Answer: 50)
-
Percentage Increase/Decrease: Calculating percentage changes is crucial for analyzing trends and growth. This involves finding the difference between two values and expressing that difference as a percentage of the original value. For example, if a price increases from $10 to $12, the percentage increase is 20%.
-
Compound Interest: Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, requires a solid grasp of percentage calculations. This is crucial for understanding long-term investments and loan repayments.
-
Tax Calculations: Calculating various types of taxes, including income tax, sales tax, and property tax, relies heavily on percentage calculations. Different tax brackets and tax rates often involve intricate percentage calculations.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate percentages?
A: The easiest method is usually converting the percentage to a decimal and multiplying it by the number you're finding the percentage of.
Q: Are there any online calculators for percentages?
A: Yes, numerous online percentage calculators are readily available. These tools can be particularly helpful for complex calculations or when you need quick results.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various examples, using different methods to solve the same problems. Focus on understanding the underlying concepts, not just memorizing formulas.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include incorrectly converting percentages to decimals, misplacing decimal points during multiplication, and failing to understand the context of the problem. Careful attention to detail is crucial.
Conclusion: Mastering the Power of Percentages
Calculating 15% of 25, while seemingly simple, serves as a gateway to understanding the broader world of percentage calculations. Mastering these calculations empowers you to navigate various aspects of your personal and professional life more effectively. By understanding the different methods and their applications, you can confidently tackle any percentage problem, from simple calculations to complex financial analyses. The ability to work with percentages is a crucial skill that will serve you well in numerous aspects of life. Remember to practice regularly and apply your knowledge to real-world scenarios to solidify your understanding and build confidence in your numerical abilities. The seemingly small skill of calculating percentages unlocks a world of analytical power and informed decision-making.
Latest Posts
Latest Posts
-
46 Kilos In Stone
Sep 14, 2025
-
45 Degrees To Rad
Sep 14, 2025
-
128 F In C
Sep 14, 2025
-
80 Inches To Feet
Sep 14, 2025
-
Foreshadowing In The Outsiders
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.