15 Percent Of 70
renascent
Sep 16, 2025 · 5 min read
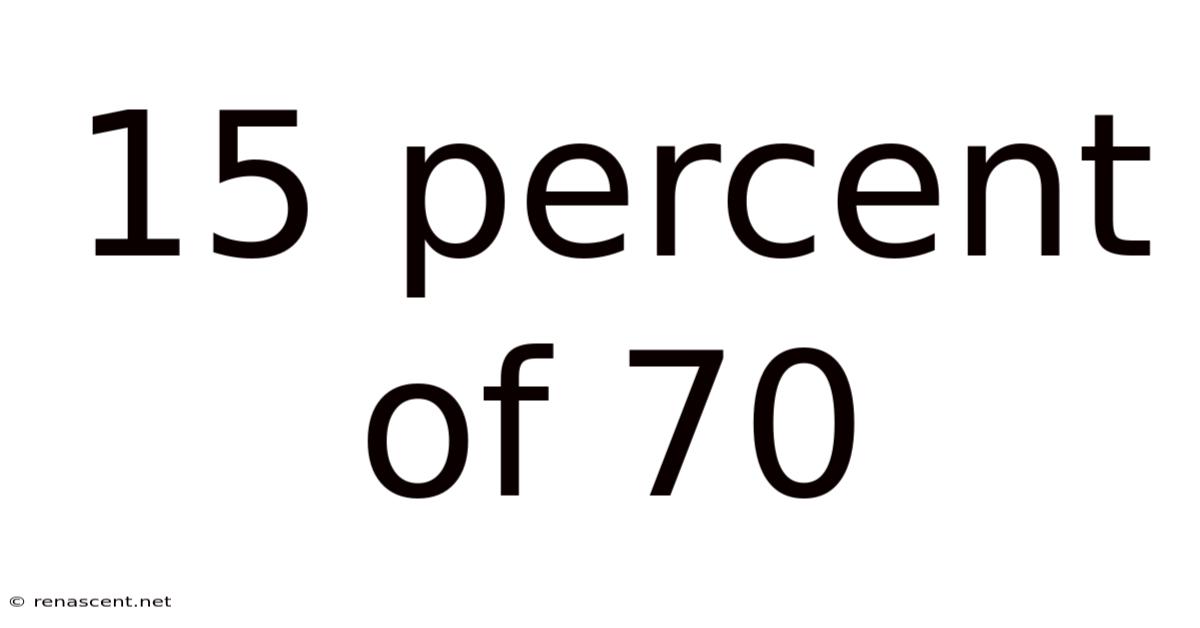
Table of Contents
Unlocking the Power of Percentages: A Deep Dive into Calculating 15% of 70
Finding 15% of 70 might seem like a simple arithmetic problem, but it's a gateway to understanding a fundamental concept crucial in various aspects of life – percentages. This seemingly small calculation underlies everything from calculating sales tax and discounts to understanding financial reports and analyzing statistical data. This article will not only show you how to calculate 15% of 70 using various methods but also delve into the broader understanding of percentages, their applications, and the importance of mastering this fundamental skill.
Understanding Percentages: The Foundation
Before we tackle the specific problem of finding 15% of 70, let's establish a solid understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." So, 15% means 15 out of 100, or 15/100. This fraction can be simplified to 3/20. Understanding this fundamental relationship is key to solving any percentage problem.
Method 1: Converting Percentage to Decimal
The most straightforward method involves converting the percentage into its decimal equivalent. To do this, we divide the percentage by 100. In our case:
15% ÷ 100 = 0.15
Now, we simply multiply this decimal by the number we're interested in (70):
0.15 * 70 = 10.5
Therefore, 15% of 70 is 10.5. This method is efficient and easily adaptable to various percentage calculations.
Method 2: Using Fractions
As mentioned earlier, 15% can be represented as the fraction 15/100 or its simplified form, 3/20. Using this fractional representation, we can calculate 15% of 70 as follows:
(3/20) * 70
We can simplify this expression by canceling out common factors:
(3/20) * 70 = (3 * 70) / 20 = 210 / 20 = 10.5
Again, we arrive at the answer: 15% of 70 is 10.5. This method emphasizes the underlying fractional nature of percentages.
Method 3: Proportion Method
This method utilizes the concept of proportionality. We set up a proportion where we equate the ratio of the percentage to 100 with the ratio of the unknown value (x) to the total value (70):
15/100 = x/70
To solve for x, we cross-multiply:
15 * 70 = 100 * x
1050 = 100x
x = 1050 / 100 = 10.5
This method reinforces the relationship between percentages and ratios and provides a structured approach to solving percentage problems.
Method 4: Using a Calculator
Modern calculators make percentage calculations incredibly easy. Most calculators have a percentage key (%). Simply enter 70, press the multiplication key (*), enter 15, and press the percentage key (%). The calculator will automatically perform the calculation and display the result: 10.5. This is the quickest method, particularly for more complex percentage calculations.
Real-World Applications of Percentage Calculations
The seemingly simple calculation of 15% of 70 has far-reaching applications in numerous real-world scenarios:
-
Sales and Discounts: Imagine a store offering a 15% discount on an item priced at $70. Using our calculation, the discount amount is $10.50, making the final price $59.50. Understanding percentage discounts is crucial for savvy shoppers.
-
Tax Calculations: Sales tax is often expressed as a percentage. If the sales tax in your area is 15%, you would pay $10.50 in tax on a $70 item.
-
Financial Analysis: Percentage changes are widely used in finance to track growth or decline in investments, profits, or expenses. Understanding these changes is vital for informed financial decisions.
-
Statistical Analysis: Percentages are essential for representing data in a clear and concise manner. For example, if 15% of 70 survey respondents answered "yes" to a particular question, this indicates that 10.5 respondents provided a "yes" answer.
-
Grade Calculations: In many educational systems, grades are often expressed as percentages. If a student scores 15 out of a possible 70 points on a test, their percentage score is calculated similarly.
Expanding Your Understanding: Beyond the Basics
While calculating 15% of 70 is a straightforward task, it serves as a stepping stone to mastering more complex percentage problems. Consider these extensions:
-
Calculating Percentage Increase or Decrease: Instead of simply finding a percentage of a number, you might need to calculate the percentage change between two numbers. For example, if a price increases from $70 to $80, what is the percentage increase?
-
Finding the Original Value: You might know the final value after a percentage increase or decrease and need to determine the original value. For instance, if a price is $59.50 after a 15% discount, what was the original price?
-
Compounding Percentages: In scenarios involving interest or growth, percentages can compound over time. Understanding how to calculate compound percentages is crucial in various financial applications.
Frequently Asked Questions (FAQ)
-
What is the easiest way to calculate percentages? Using a calculator is generally the quickest and easiest method, especially for complex calculations. However, understanding the underlying principles (converting percentages to decimals or fractions) is essential for problem-solving.
-
Why are percentages important? Percentages provide a standardized and easily understandable way to represent parts of a whole. They are used extensively in various fields, including finance, statistics, and everyday life.
-
Can I calculate percentages without a calculator? Yes, absolutely! You can use the decimal or fraction method to calculate percentages manually.
Conclusion: Mastering Percentages – A Lifelong Skill
Calculating 15% of 70, while seemingly trivial, is a valuable exercise in understanding the fundamental concept of percentages. This skill transcends simple arithmetic; it's a crucial tool applicable across numerous domains. By mastering the various methods presented here and exploring the related concepts, you'll equip yourself with a powerful skill applicable throughout your life, both personally and professionally. The ability to quickly and accurately calculate percentages is not just a mathematical skill; it's a practical life skill that enhances your ability to interpret data, make informed decisions, and navigate the numerical world around you. So, embrace the power of percentages – they are much more than just numbers; they are a key to unlocking deeper understanding and informed decision-making.
Latest Posts
Latest Posts
-
16 9 Oz To Ml
Sep 16, 2025
-
465 As A Fraction
Sep 16, 2025
-
Early Sunday Morning Painting
Sep 16, 2025
-
2 3 Of 17
Sep 16, 2025
-
91 6 Kg In Pounds
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.