15 Percent Off 64
renascent
Sep 20, 2025 · 5 min read
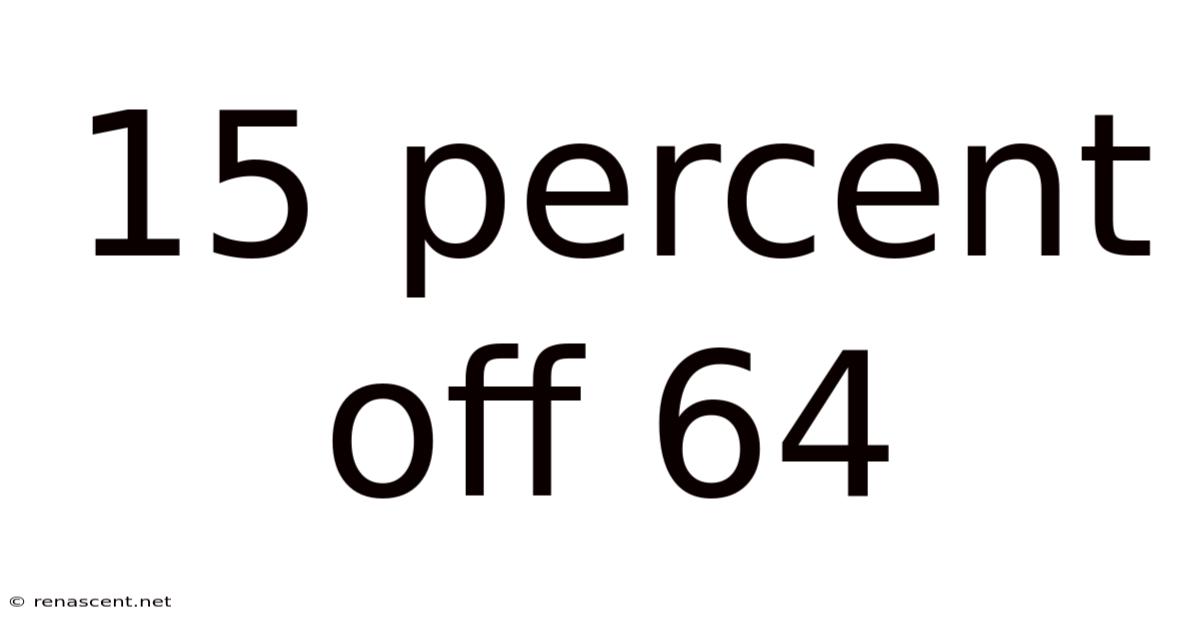
Table of Contents
Decoding the Discount: Understanding 15% Off 64
Calculating discounts is a fundamental skill in everyday life, from shopping for groceries to managing personal finances. Understanding how discounts work, especially percentage-based ones, empowers you to make informed decisions and save money. This article dives deep into the calculation of a 15% discount on 64, explaining the process step-by-step, exploring different calculation methods, and addressing common misconceptions. We will also explore the broader application of percentage calculations and how to confidently navigate similar scenarios in various contexts.
Understanding Percentage Discounts
A percentage discount represents a reduction in the original price of an item or service. It's expressed as a fraction of 100, indicating the amount of reduction relative to the original price. For example, a 15% discount means you'll pay 85% (100% - 15%) of the original price. The core concept lies in converting the percentage into a decimal and then applying it to the original value.
Calculating 15% Off 64: A Step-by-Step Guide
Let's break down the calculation of a 15% discount on 64 using several methods.
Method 1: Finding the Discount Amount First
-
Convert the percentage to a decimal: Divide the percentage by 100. In this case, 15% / 100 = 0.15.
-
Calculate the discount amount: Multiply the original price by the decimal equivalent of the percentage. This gives us 64 * 0.15 = 9.6. This means the discount is $9.60.
-
Calculate the final price: Subtract the discount amount from the original price. Therefore, 64 - 9.6 = 54.4. The final price after a 15% discount is $54.40.
Method 2: Finding the Percentage Remaining Directly
This method is slightly faster and avoids an intermediate step.
-
Calculate the percentage remaining: If the discount is 15%, then the remaining percentage is 100% - 15% = 85%.
-
Convert the percentage remaining to a decimal: 85% / 100 = 0.85.
-
Calculate the final price directly: Multiply the original price by the decimal equivalent of the remaining percentage. This gives us 64 * 0.85 = 54.4. The final price is again $54.40.
Alternative Calculation Methods
While the methods above are straightforward, other approaches exist, particularly useful with more complex scenarios or when using calculators with limited functionality.
Method 3: Using Fractions
Percentages can be represented as fractions. 15% can be written as 15/100, which simplifies to 3/20.
-
Express the percentage as a fraction: 15% = 3/20
-
Calculate the discount: Multiply the original price by the fraction: 64 * (3/20) = 9.6. This represents the discount amount ($9.60).
-
Calculate the final price: Subtract the discount from the original price: 64 - 9.6 = 54.4. The final price remains $54.40.
Method 4: Using Proportions
Proportions offer another approach to solving percentage problems.
-
Set up a proportion: Let 'x' represent the discount amount. We can set up the proportion: 15/100 = x/64
-
Solve for x: Cross-multiply and solve the equation: 100x = 15 * 64 => 100x = 960 => x = 9.6. This again yields the discount amount of $9.60.
-
Calculate the final price: Subtract the discount from the original price: 64 - 9.6 = 54.4. The final price is $54.40.
Practical Applications and Real-World Scenarios
Understanding percentage discounts is vital in many everyday situations:
-
Shopping: Identifying the best deals, comparing prices from different stores, and maximizing savings during sales.
-
Finance: Calculating interest on loans, savings accounts, and investments. Understanding tax deductions and other financial adjustments based on percentages.
-
Sales and Marketing: Analyzing sales data, calculating profit margins, and setting pricing strategies based on desired profit percentages.
-
Statistics and Data Analysis: Interpreting data presented as percentages, calculating percentages of change, and understanding statistical significance.
Common Mistakes and Misconceptions
Several common errors can occur when calculating percentage discounts:
-
Incorrect decimal conversion: Failing to correctly convert the percentage to a decimal (e.g., using 15 instead of 0.15) leads to significantly inaccurate results.
-
Adding the discount instead of subtracting: The discount amount must be subtracted from the original price to find the final price, not added.
-
Calculating the discount on the discounted price: Applying a second discount on an already discounted price will lead to an incorrect final price. Each discount should be calculated sequentially based on the previous price.
-
Confusing percentage increase and decrease: Understanding the difference between calculating a percentage increase (adding to the original value) and a percentage decrease (subtracting from the original value) is crucial.
Frequently Asked Questions (FAQs)
Q: What if the original price wasn't a whole number?
A: The calculation methods remain the same. You'll simply work with decimal numbers throughout the process. For example, if the original price was 64.50, you would multiply 64.50 by 0.15 to find the discount amount.
Q: Can I use a calculator to solve this?
A: Absolutely! Calculators make the process much faster. Simply input the calculations as described in the methods above.
Q: How do I calculate multiple discounts?
A: For multiple discounts, you apply them sequentially. Don't simply add the percentages together. Calculate the first discount, then apply the second discount to the resulting price, and so on.
Q: What if I need to calculate the original price from a discounted price?
A: To find the original price, work backward. If the discounted price is 54.4 and the discount was 15%, this means 85% of the original price is 54.4. Divide the discounted price by the remaining percentage (0.85) to get the original price: 54.4 / 0.85 = 64.
Q: Are there any online tools to help with this calculation?
A: Many websites offer percentage calculators that can automate the process, saving you manual calculation time. However, understanding the underlying concepts is crucial for applying this knowledge in various situations.
Conclusion
Calculating a 15% discount on 64, or any similar percentage discount problem, involves a straightforward process. By understanding the different methods and avoiding common pitfalls, you can confidently calculate discounts in various real-world contexts. This ability extends far beyond simple shopping scenarios, contributing to better financial literacy and informed decision-making in numerous aspects of life. Mastering these fundamental calculations empowers you to become a more astute consumer, a more effective financial manager, and a more insightful problem-solver. Remember, the key is to break down the problem into smaller, manageable steps and to double-check your work to avoid errors. With practice, these calculations will become second nature, enhancing your numerical fluency and empowering you to navigate the world of percentages with ease and confidence.
Latest Posts
Latest Posts
-
230 Lbs In Kg
Sep 20, 2025
-
6 10 As A Percentage
Sep 20, 2025
-
63 Degrees Fahrenheit Celsius
Sep 20, 2025
-
45 Percent Of 30
Sep 20, 2025
-
4600 Divided By 20
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent Off 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.