16 X 2 0
renascent
Sep 18, 2025 · 6 min read
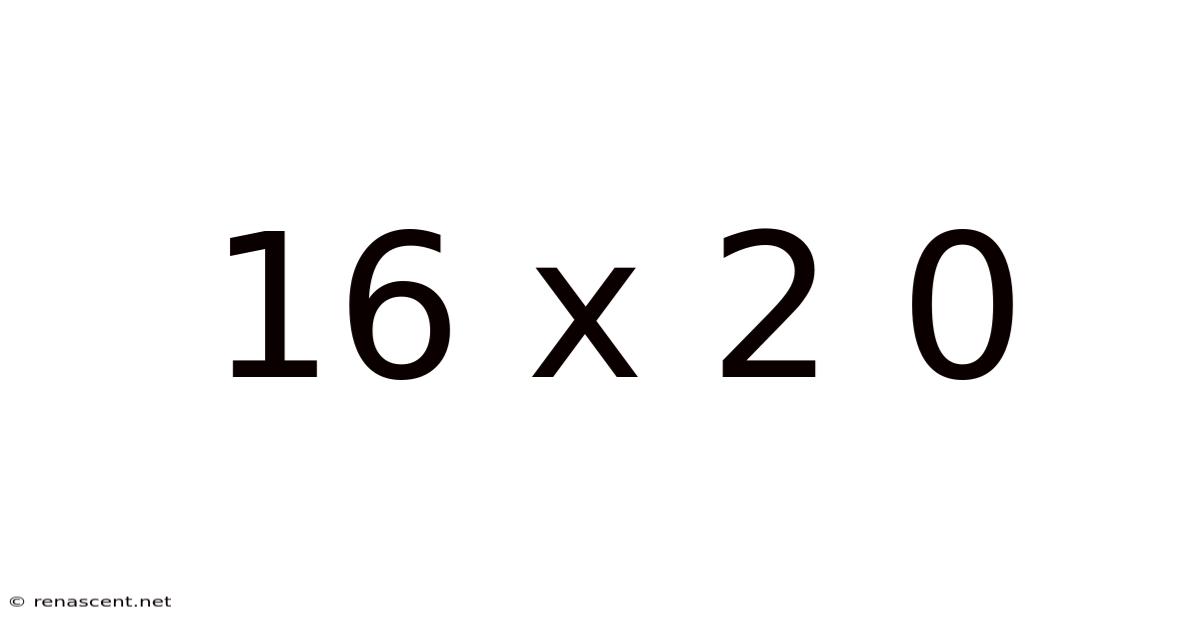
Table of Contents
Decoding 16 x 20: A Deep Dive into the Mathematics and Applications of Rectangular Dimensions
The seemingly simple expression "16 x 20" represents far more than just two numbers multiplied together. It signifies a rectangular area, a fundamental concept in mathematics with widespread applications in various fields, from construction and design to data analysis and computer graphics. This article will explore the mathematical underpinnings of 16 x 20 dimensions, delve into its practical applications, and uncover some of its less obvious implications. We'll cover everything from calculating area and perimeter to understanding scale and proportion, ultimately showing how this seemingly simple expression underpins a wealth of complex concepts.
Understanding the Fundamentals: Area and Perimeter
The core mathematical concepts associated with 16 x 20 are area and perimeter. The dimensions 16 and 20 represent the length and width (or vice-versa) of a rectangle.
-
Area: The area of a rectangle is calculated by multiplying its length by its width. In this case, the area of a 16 x 20 rectangle is 16 x 20 = 320 square units. The units could be square inches, square feet, square meters, or any other appropriate unit of area, depending on the context.
-
Perimeter: The perimeter of a rectangle is the total distance around its edges. It's calculated by adding up the lengths of all four sides: 2(length + width). For a 16 x 20 rectangle, the perimeter is 2(16 + 20) = 72 units. Again, the units depend on the context (inches, feet, meters, etc.).
Understanding these basic calculations is crucial for any application involving rectangular dimensions. Whether you're calculating the amount of paint needed for a wall, the space required for furniture, or the size of a digital image, knowing how to find area and perimeter is essential.
Applications Across Various Disciplines
The 16 x 20 dimensions, or variations thereof, appear in a surprisingly broad range of applications:
1. Construction and Architecture:
- Room dimensions: A 16 x 20 foot room is a common size for bedrooms, living rooms, or smaller offices. Understanding these dimensions is crucial for floor planning, furniture placement, and material estimation.
- Building footprints: The footprint of a building, especially smaller structures like garages or sheds, might be based on 16 x 20 feet or a multiple thereof.
- Land surveying: Land parcels often have dimensions expressed in feet or meters, and understanding rectangular areas is essential for calculating land area and property boundaries.
2. Graphic Design and Image Processing:
- Image dimensions: While not a standard aspect ratio for photography, 16 x 20 might represent the dimensions of a digital image in pixels or other units. Understanding these dimensions is crucial for image scaling, resizing, and printing.
- Print design: Many print designs, especially posters or brochures, might use dimensions based on multiples of 16 and 20, depending on the desired aspect ratio and the print medium.
- Web design: While less common for screen resolutions, understanding rectangular dimensions allows for proportional scaling of web elements.
3. Data Analysis and Statistics:
- Data matrices: In data analysis, a 16 x 20 matrix could represent a dataset with 16 rows and 20 columns. Understanding the dimensions of such a matrix is crucial for various statistical operations.
- Spreadsheets: A spreadsheet with 16 rows and 20 columns provides a structured way to organize and analyze data.
- Image processing algorithms: Image processing often involves manipulating rectangular arrays of pixel data, where dimensions like 16 x 20 are frequently encountered.
4. Manufacturing and Production:
- Product dimensions: Many manufactured products, from packaging to components, have dimensions that are multiples or fractions of 16 x 20, depending on the design and manufacturing constraints.
- Material cutting: Efficient material cutting requires careful consideration of dimensions to minimize waste. Understanding rectangular area calculation ensures optimal utilization of materials.
- Assembly line planning: The dimensions of workspaces and component arrangements often rely on rectangular measurements to ensure efficient workflows.
Exploring Scale and Proportion
Beyond the basic calculations of area and perimeter, the 16 x 20 dimensions also illustrate concepts of scale and proportion. The ratio of 16:20 can be simplified to 4:5. This ratio can be scaled up or down to maintain the same proportions. For instance:
- Scaling up: A 32 x 40 rectangle maintains the same 4:5 ratio as a 16 x 20 rectangle, simply doubling the dimensions.
- Scaling down: An 8 x 10 rectangle also maintains the 4:5 ratio, halving the original dimensions.
Understanding these scaling properties is crucial for maintaining the aspect ratio of designs, images, or models when resizing or adjusting their dimensions. This is especially important in fields like architecture and graphic design, where maintaining visual consistency is crucial.
The Mathematical Significance of Rectangles
The rectangle, represented by dimensions like 16 x 20, is a fundamental geometric shape with a rich history in mathematics. Its properties have been studied for centuries, leading to advancements in areas like:
- Euclidean geometry: Rectangles are a cornerstone of Euclidean geometry, with properties like parallel sides and right angles forming the basis of many theorems and proofs.
- Coordinate geometry: Rectangles can be easily represented in coordinate systems, allowing for precise calculations of area, perimeter, and other properties.
- Calculus: Rectangles are used to approximate areas under curves in integral calculus, a fundamental concept in higher mathematics.
The simplicity of the rectangle's definition belies its importance in a wide range of mathematical contexts.
Beyond the Basics: Advanced Applications
While the basic calculations for area and perimeter are straightforward, the applications of 16 x 20 dimensions can extend to more complex scenarios:
- Three-dimensional applications: Imagine a rectangular prism with a base of 16 x 20. Adding a third dimension (height) allows for calculations of volume and surface area, crucial in fields like packaging design and construction.
- Optimization problems: Consider maximizing the area of a rectangle given a fixed perimeter. This type of optimization problem frequently arises in engineering and design, requiring a deeper understanding of geometric relationships.
- Advanced statistical analysis: In statistical analysis, the 16 x 20 dimensions might represent the dimensions of a covariance matrix or a correlation matrix, leading to more complex calculations.
These more advanced applications demonstrate how a seemingly simple concept, such as the dimensions 16 x 20, can serve as a foundation for much more complex mathematical modeling and problem-solving.
Frequently Asked Questions (FAQ)
-
Q: What are the different units I can use for 16 x 20 dimensions?
- A: The units depend on the context. It could be inches, feet, meters, centimeters, pixels, or any other relevant unit of measurement.
-
Q: How do I convert 16 x 20 feet to square meters?
- A: First, convert feet to meters (1 foot ≈ 0.3048 meters). Then, calculate the area in square meters.
-
Q: Can I use 16 x 20 for landscape orientation as well?
- A: Yes, the orientation (landscape or portrait) simply changes which dimension is considered the length and which is the width. The area and perimeter calculations remain the same.
Conclusion
The seemingly simple expression "16 x 20" represents a rich tapestry of mathematical concepts and practical applications. From the fundamental calculations of area and perimeter to the more sophisticated concepts of scale, proportion, and optimization, the 16 x 20 dimensions provide a compelling illustration of how basic mathematical principles underpin a vast array of fields. Understanding these dimensions and their underlying principles is valuable across a broad range of disciplines, highlighting the enduring relevance of fundamental mathematical concepts in our world. Whether you're a student, designer, engineer, or simply curious about the world around you, appreciating the implications of 16 x 20 opens up a deeper understanding of the mathematical structures that shape our reality.
Latest Posts
Latest Posts
-
Winkel Tripel Map Projection
Sep 18, 2025
-
0 4 Kg To Grams
Sep 18, 2025
-
Questions On Compound Interest
Sep 18, 2025
-
175 Divided By 5
Sep 18, 2025
-
Meaning Of Mitigating Factors
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 16 X 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.