17/50 As A Percentage
renascent
Sep 25, 2025 · 5 min read
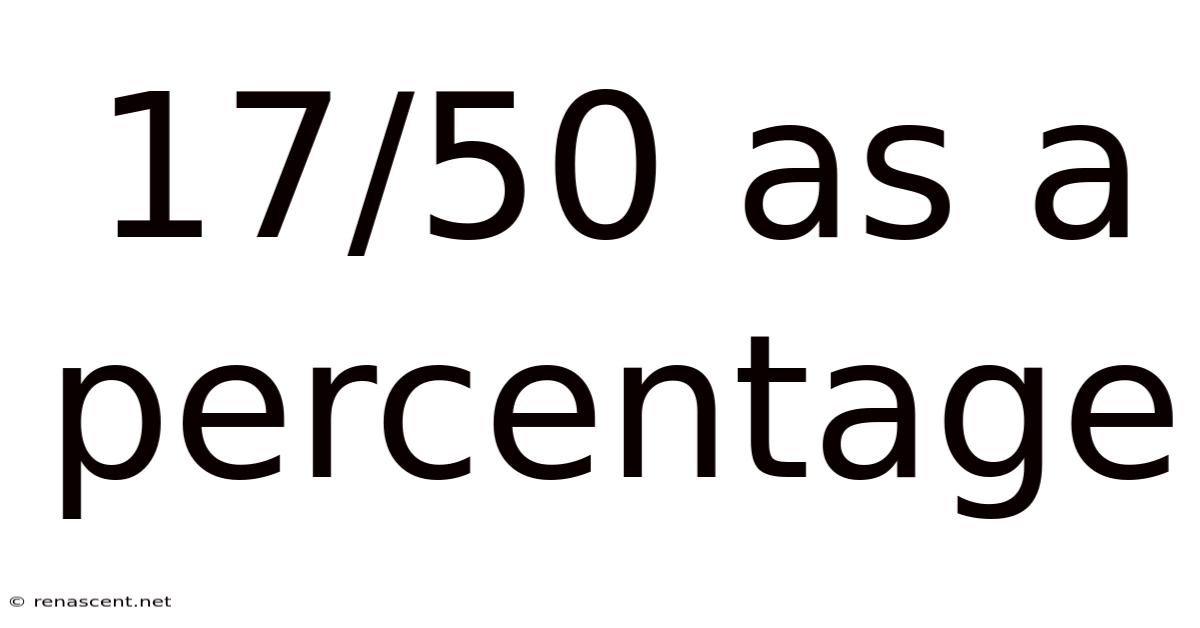
Table of Contents
Understanding 17/50 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax to understanding statistics and financial reports. This article will thoroughly explore how to convert the fraction 17/50 into a percentage, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also explore practical examples and address frequently asked questions to ensure a complete understanding of this concept.
Introduction: Fractions, Decimals, and Percentages
Before diving into the conversion of 17/50, let's briefly review the relationships between fractions, decimals, and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator/denominator). A decimal is a way of expressing a fraction using base-10, with a decimal point separating the whole number from the fractional part. A percentage is a way of expressing a fraction or decimal as a portion of 100, denoted by the symbol %.
These three representations are interchangeable. For example, 1/2 can be represented as 0.5 or 50%. Understanding this interchangeability is crucial for various mathematical operations and real-world problem-solving.
Converting 17/50 to a Percentage: The Step-by-Step Process
There are two primary methods for converting the fraction 17/50 to a percentage:
Method 1: Converting the Fraction to a Decimal First
This method involves two steps:
-
Convert the fraction to a decimal: To do this, we divide the numerator (17) by the denominator (50):
17 ÷ 50 = 0.34
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.34 × 100 = 34%
Therefore, 17/50 is equal to 34%.
Method 2: Direct Conversion using Proportion
This method utilizes the definition of percentage as a part of 100. We set up a proportion:
17/50 = x/100
To solve for 'x' (the percentage), we cross-multiply:
50x = 1700
Then, we divide both sides by 50:
x = 1700 ÷ 50 = 34
Therefore, x = 34, meaning 17/50 is equal to 34%.
Why These Methods Work: A Deeper Mathematical Look
The reason these methods work lies in the fundamental relationships between fractions, decimals, and percentages. Percentages are essentially fractions with a denominator of 100. When we divide the numerator of a fraction by its denominator, we obtain its decimal equivalent. Multiplying this decimal by 100 is equivalent to scaling the fraction to have a denominator of 100, thus giving us the percentage.
The proportion method directly establishes this relationship, setting up an equation where we solve for the equivalent value when the denominator is 100. Both methods achieve the same result, providing alternative approaches based on mathematical principles.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages has numerous practical applications across various fields:
-
Finance: Calculating interest rates, discounts, tax percentages, and profit margins. For example, a 34% discount on a $100 item would be a savings of $34.
-
Statistics: Representing data as percentages to facilitate comparisons and analysis. For instance, if 17 out of 50 students passed an exam, the pass rate is 34%.
-
Science: Expressing experimental results and probabilities as percentages. A 34% chance of rain indicates a significant probability of precipitation.
-
Everyday Life: Calculating tips, determining sale prices, and understanding survey results. Knowing that 17/50 is 34% allows for quick mental calculations in various scenarios.
Illustrative Examples Using 17/50 and 34%
Let's illustrate the practical application of converting 17/50 to 34% with a few examples:
Example 1: Sales Discount
A store offers a 34% discount on all items. If an item costs $200, the discount amount is:
$200 × 0.34 = $68
The final price after the discount would be:
$200 - $68 = $132
Example 2: Exam Results
In a class of 50 students, 17 students scored above 90%. The percentage of students who scored above 90% is 34%.
Example 3: Survey Results
A survey of 50 people shows that 17 prefer a particular brand of coffee. The percentage of people who prefer that brand is 34%.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A1: Yes, any fraction can be converted to a percentage by following the methods outlined above.
Q2: What if the fraction results in a repeating decimal?
A2: If the division results in a repeating decimal, you can round the decimal to a certain number of decimal places before converting it to a percentage. For example, 1/3 = 0.333... Rounding to two decimal places gives 0.33, which is 33%.
Q3: Are there any online calculators or tools that can help with this conversion?
A3: Yes, many online calculators and tools are available to perform fraction-to-percentage conversions quickly and accurately. However, understanding the underlying mathematical process is crucial for developing a solid understanding of the concept.
Q4: Why is understanding percentages important?
A4: Percentages are a fundamental tool for comparing quantities, expressing proportions, and understanding data in various contexts. They are used extensively in finance, statistics, science, and everyday life.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a vital mathematical skill with broad applications. The conversion of 17/50 to 34% exemplifies the straightforward process involved, whether using the decimal conversion method or the direct proportion method. By understanding the underlying mathematical principles and practicing with various examples, you can confidently perform these conversions and apply this knowledge to real-world situations. Remember, the ability to convert between fractions, decimals, and percentages is a key component of numerical literacy, enabling you to effectively interpret and analyze data across various fields. Mastering this skill provides you with a valuable tool for understanding and navigating the quantitative aspects of our world.
Latest Posts
Latest Posts
-
Ethanoic Acid Sodium Carbonate
Sep 25, 2025
-
Bel Canto Opera Style
Sep 25, 2025
-
Advantages To Selective Breeding
Sep 25, 2025
-
41 Degrees To Fahrenheit
Sep 25, 2025
-
Conjugate The Verb Vivir
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 17/50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.