17 Divided By 4
renascent
Sep 24, 2025 · 5 min read
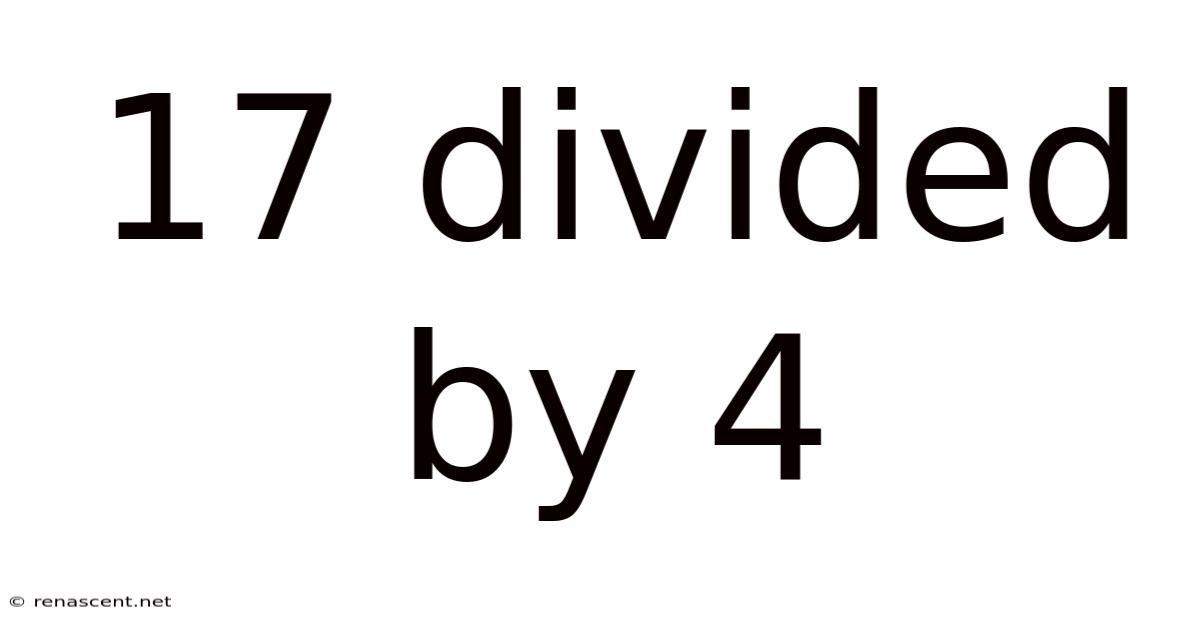
Table of Contents
Unveiling the Mystery: 17 Divided by 4 – A Deep Dive into Division
Dividing 17 by 4 might seem like a simple arithmetic problem, suitable only for elementary school students. However, a closer examination reveals a rich tapestry of mathematical concepts, highlighting the elegance and versatility of the division operation. This article will delve into the intricacies of 17 ÷ 4, exploring its various representations, the underlying principles, and its applications in real-world scenarios. We'll cover everything from the basic calculation to advanced interpretations, ensuring a comprehensive understanding for readers of all levels.
Understanding the Problem: 17 ÷ 4
The problem 17 ÷ 4 asks: "How many times does 4 fit into 17?" This seemingly straightforward question leads to a result that isn't a whole number, introducing us to the world of fractions and decimals. Understanding this fundamental concept is crucial for grasping the subsequent explanations.
The Basic Calculation: Quotient and Remainder
Performing the division, we find that 4 goes into 17 four times (4 x 4 = 16). This is our quotient. However, we have 1 left over, which is our remainder. Therefore, we can represent the result as:
- 4 remainder 1
This representation is perfectly valid and often the most practical answer, particularly when dealing with discrete objects. For example, if you have 17 apples and want to divide them equally among 4 people, each person gets 4 apples, and you have 1 apple left over.
Expressing the Result as a Fraction
The remainder doesn't tell the whole story. We can express the leftover portion as a fraction, representing the part of a whole. Since we had 1 leftover out of a group of 4, the fractional representation is:
- 4 1/4 (Four and one-quarter)
This mixed number combines the whole number quotient (4) with the fractional remainder (1/4). This offers a more precise and complete picture than simply stating the remainder.
Decimal Representation: Bringing in Precision
While fractions provide precision, decimal numbers offer another level of clarity, particularly in scenarios requiring calculations involving other numbers. To convert the fraction 1/4 to a decimal, we perform the division: 1 ÷ 4 = 0.25. This gives us the decimal representation of 17 ÷ 4:
- 4.25 (Four and twenty-five hundredths)
This representation is particularly useful for calculations that involve further arithmetic operations. For example, if we need to multiply the result by another number, using the decimal form simplifies the process.
Visual Representation: Understanding Division Geometrically
Visualizing the division can enhance understanding. Imagine a rectangle with an area of 17 square units. We want to divide this rectangle into four equal parts. We can fit four squares of side length 4 units within the rectangle (representing 4 x 4 = 16 square units), leaving a small rectangle of 1 square unit. This leftover square unit visually represents the remainder. This geometric representation reinforces the concept of the quotient and remainder.
Real-World Applications: Where Division Matters
The division of 17 by 4 isn't just an abstract mathematical exercise. It pops up in various real-world scenarios:
-
Resource Allocation: Dividing resources among a group of people. If you have 17 cookies to share amongst 4 friends, each friend gets 4 cookies, and you keep 1.
-
Measurement and Conversion: Converting units of measurement often involves division. For example, converting 17 inches into groups of 4 inches each.
-
Average Calculation: Finding the average score on a test where a group of 4 students have scores adding up to 17.
-
Pricing and Discounts: Calculating the price per unit or the discounted price after a percentage reduction might involve a division such as this.
Exploring the Concept Further: Beyond Basic Division
17 ÷ 4 also provides a springboard to explore more advanced mathematical concepts:
-
Long Division: The process of long division provides a systematic approach to handling larger numbers and complex divisions. This method allows for a step-by-step breakdown of the division process.
-
Algebraic Division: In algebra, dividing polynomials involves similar principles as the division of numbers. Understanding the concept of division in the context of numbers forms a solid foundation for algebraic manipulations.
-
Modular Arithmetic: The remainder (1 in this case) plays a crucial role in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). The remainder is the key element in this type of calculation.
Frequently Asked Questions (FAQs)
Q: Can you explain the difference between a quotient and a remainder?
A: The quotient is the whole number result of a division. It represents how many times the divisor (the number you are dividing by) fits completely into the dividend (the number being divided). The remainder is the amount left over after the complete divisions.
Q: Why are both the fractional and decimal representations important?
A: The fractional representation (4 1/4) provides a precise representation of the division, highlighting the leftover portion as a fraction of the whole. The decimal representation (4.25) offers a format suitable for further mathematical operations and comparisons.
Q: What are some other methods to calculate 17 divided by 4 besides long division?
A: Besides long division, you can use a calculator, mental math techniques (if you are familiar with fractions and decimals), or even repeated subtraction (subtracting 4 from 17 until you reach a number less than 4).
Q: Is there a way to express the result as a percentage?
A: Yes. If you want to express the result as a percentage of the total (17), you would calculate (17 ÷ 4) ÷ 17 x 100%. This would give you the percentage that 4 is of 17. Conversely, to find what percentage of 17 is 4, you'd calculate 4/17 x 100%.
Conclusion: More Than Just a Simple Calculation
The seemingly simple problem of 17 divided by 4 offers a pathway to a deeper understanding of division, fractions, decimals, and their applications in the real world. By exploring its different representations and interpretations, we uncover the underlying principles that govern this fundamental arithmetic operation. Mastering this seemingly basic concept serves as a strong foundation for tackling more complex mathematical problems. Remember, math is not just about numbers; it's about understanding the relationships between them and applying that understanding to solve problems in diverse contexts.
Latest Posts
Latest Posts
-
3370 Grams To Pounds
Sep 24, 2025
-
1 4 Of 14
Sep 24, 2025
-
1080 Divided By 4
Sep 24, 2025
-
4 And 8 Lcm
Sep 24, 2025
-
Feeling Of Ill Will
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 17 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.