177 Divided By 6
renascent
Sep 21, 2025 · 5 min read
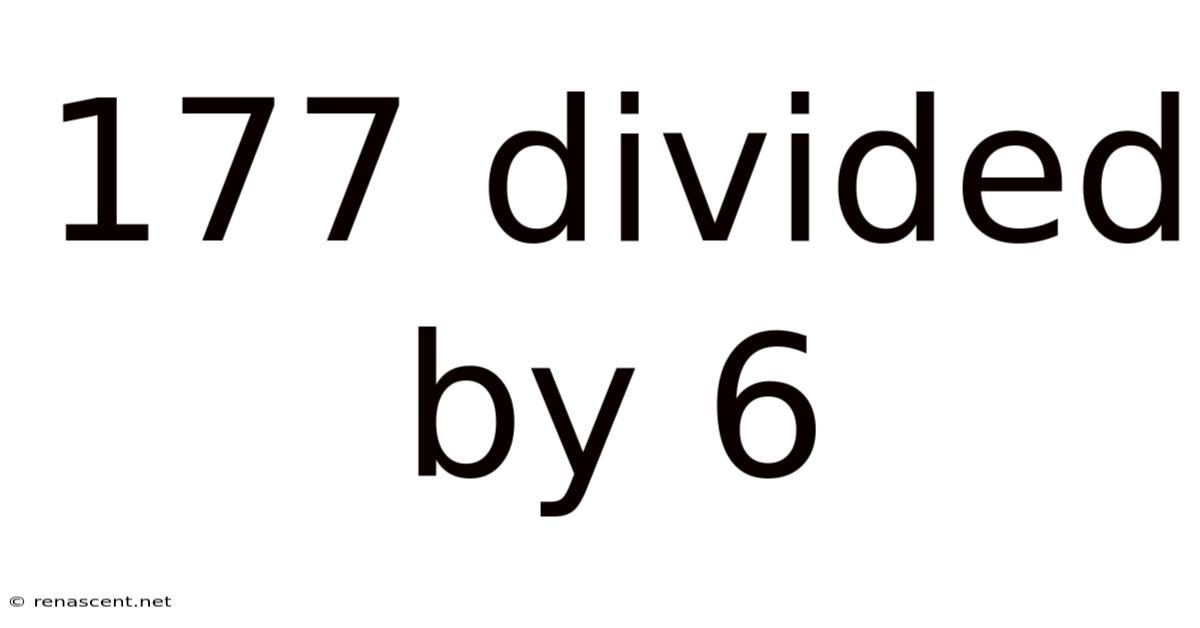
Table of Contents
Unpacking 177 Divided by 6: A Deep Dive into Division
Dividing 177 by 6 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a fantastic opportunity to explore several crucial mathematical concepts, from basic division to the nuances of remainders and their practical applications. This article will delve into the process of dividing 177 by 6, providing a comprehensive understanding accessible to all, regardless of their mathematical background. We will examine the solution through various methods, discuss the significance of the remainder, and explore real-world scenarios where such calculations are relevant.
Understanding the Problem: 177 ÷ 6
The core of the problem, 177 ÷ 6, asks: "How many times does 6 fit into 177?" This seemingly simple question lays the foundation for a deeper understanding of division as a process of repeated subtraction or the inverse operation of multiplication. It's not just about finding a numerical answer; it's about grasping the underlying mathematical principles. We will dissect this problem using different approaches, highlighting the conceptual underpinnings of each method.
Method 1: Long Division – The Traditional Approach
The most common method for solving this problem is long division. This method systematically breaks down the division into smaller, manageable steps. Let's walk through it:
-
Set up the problem: Write 177 inside the long division symbol (⟌) and 6 outside.
-
Divide the tens: How many times does 6 go into 17? The answer is 2 (6 x 2 = 12). Write the 2 above the 7 in 177.
-
Subtract: Subtract 12 from 17, leaving 5.
-
Bring down: Bring down the next digit (7) from 177, placing it next to the 5 to make 57.
-
Divide the ones: How many times does 6 go into 57? The answer is 9 (6 x 9 = 54). Write the 9 above the 7 in 177.
-
Subtract: Subtract 54 from 57, leaving 3.
-
Remainder: The number 3 is the remainder. This indicates that 6 goes into 177 twenty-nine times with 3 left over.
Therefore, 177 ÷ 6 = 29 with a remainder of 3. We can express this as 29 R 3 or using mixed numbers as 29 3/6, which simplifies to 29 ½.
Method 2: Repeated Subtraction
This method provides a more intuitive understanding of division. We repeatedly subtract 6 from 177 until we reach a number less than 6. Let's demonstrate:
177 - 6 = 171 171 - 6 = 165 165 - 6 = 159 ...and so on.
Continuing this process, we'll find that we subtract 6 a total of 29 times before reaching a remainder of 3. This visually reinforces the concept of division as repeated subtraction. While less efficient for larger numbers, this method clarifies the fundamental principle.
Method 3: Using Multiplication and Estimation
This method utilizes our understanding of multiplication tables to find an approximate answer and then refine it.
We know that 6 x 20 = 120 and 6 x 30 = 180. Since 177 falls between 120 and 180, we can estimate that the quotient will be between 20 and 30. Through trial and error, or by using a closer estimation (e.g., 6 x 25 = 150; 6 x 30 = 180), we can quickly approach the correct answer of 29 with a remainder of 3. This method enhances estimation skills, a valuable asset in various mathematical contexts.
The Significance of the Remainder
The remainder (3 in this case) is a crucial part of the answer and holds significant mathematical meaning. It represents the amount left over after the division is complete. In real-world applications, the remainder dictates how we interpret the result.
-
Sharing equally: If you have 177 cookies and want to share them equally among 6 friends, each friend would receive 29 cookies, and you would have 3 cookies left over.
-
Measurement: If you need to cut a 177-inch rope into 6 equal pieces, each piece would be 29 inches long, with a 3-inch piece remaining.
-
Fractions and Decimals: The remainder can be expressed as a fraction (3/6, which simplifies to ½) or a decimal (0.5). This allows for a more precise representation of the result, depending on the context.
Real-World Applications
Understanding division, including handling remainders, is essential in many everyday situations:
-
Finance: Calculating equal payments, splitting bills, or determining unit prices.
-
Cooking and Baking: Adjusting recipe quantities or dividing ingredients.
-
Construction and Engineering: Calculating material requirements or dividing spaces.
-
Data Analysis: Determining averages, ratios, or percentages.
-
Programming: Performing calculations and manipulating data within algorithms.
The seemingly simple problem of 177 divided by 6 becomes a gateway to understanding fundamental mathematical concepts and their broad applicability across diverse fields.
Frequently Asked Questions (FAQs)
-
What is the simplest form of the fraction representing the remainder? The remainder 3/6 simplifies to ½.
-
Can the remainder be expressed as a decimal? Yes, the remainder 3/6 is equivalent to 0.5.
-
Why is long division considered a standard method? Long division provides a systematic and structured approach to solving division problems, particularly those involving larger numbers.
-
Are there other methods to solve this problem? Yes, as demonstrated, repeated subtraction and estimation techniques can also be used, each offering a slightly different perspective on the division process.
-
What if we are working with negative numbers? The process of long division remains the same, although you need to be mindful of the rules governing the multiplication and subtraction of negative numbers. For example, dividing -177 by 6 would result in -29 with a remainder of -3.
Conclusion: Beyond the Numbers
Dividing 177 by 6 is more than just a simple calculation; it's a stepping stone to mastering crucial mathematical concepts. The process allows us to explore different approaches, understand the significance of remainders, and appreciate the practical applications of division in everyday life. By mastering these fundamentals, we equip ourselves with essential problem-solving skills transferable across various academic and professional domains. The beauty of mathematics lies not just in the answers, but in the journey of understanding the underlying principles and their practical implications. This exploration of 177 divided by 6 hopefully showcases that journey and inspires a deeper appreciation for the elegance and utility of mathematical concepts.
Latest Posts
Latest Posts
-
2000 Hrs To Days
Sep 21, 2025
-
Idiom For Work Hard
Sep 21, 2025
-
1 93 Metres In Feet
Sep 21, 2025
-
White Belt Blox Fruits
Sep 21, 2025
-
Alice In Wonderland Food
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 177 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.