18/30 As A Percent
renascent
Sep 16, 2025 · 5 min read
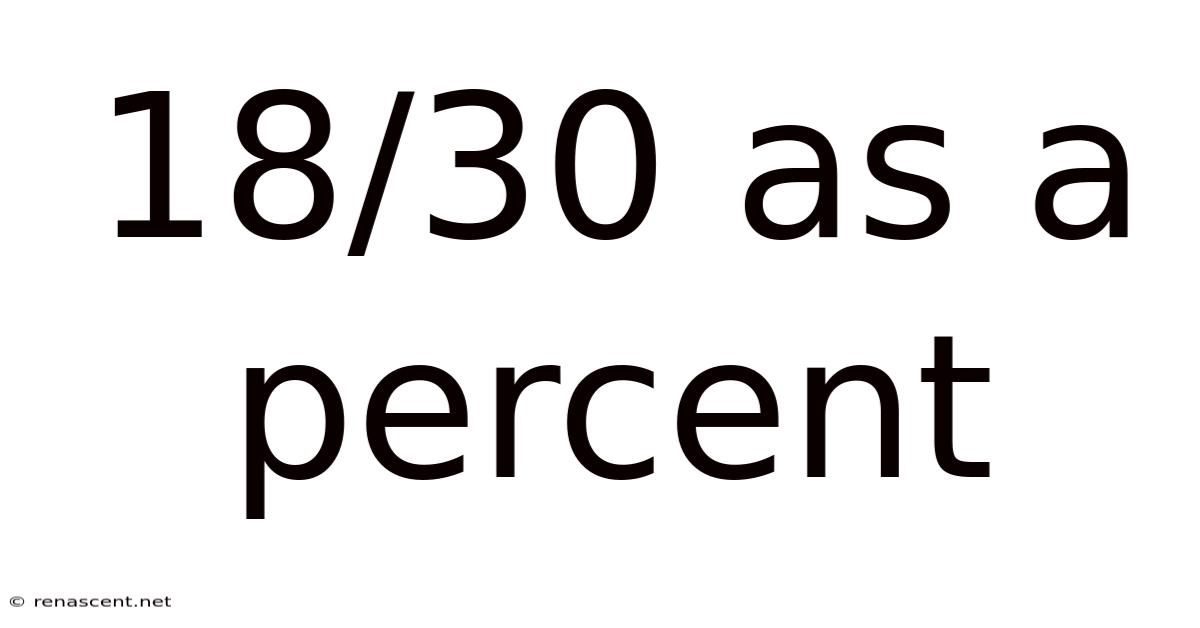
Table of Contents
Decoding 18/30 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, crucial for everyday life, from calculating discounts to understanding statistics. This comprehensive guide will delve into the conversion of the fraction 18/30 into a percentage, exploring the underlying principles, practical applications, and addressing common queries. We'll also examine related concepts to build a strong foundation in this area.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the specifics of 18/30, let's establish the relationship between fractions, decimals, and percentages. They are different ways of expressing the same value, representing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, 18/30 means 18 parts out of a total of 30 parts.
-
Decimal: A decimal is a way of expressing a fraction using a base-10 system. It uses a decimal point to separate the whole number part from the fractional part.
-
Percentage: A percentage represents a fraction or decimal as parts per hundred. The symbol "%" signifies "per cent," meaning "out of one hundred."
These three forms are interchangeable, and understanding their conversions is essential for mathematical fluency.
Converting 18/30 to a Percentage: A Step-by-Step Approach
There are several ways to convert the fraction 18/30 to a percentage. Here are two common methods:
Method 1: Simplifying the Fraction First
This method involves simplifying the fraction to its lowest terms before converting to a percentage. This simplifies the calculations and often makes the conversion easier to understand.
-
Simplify the Fraction: Find the greatest common divisor (GCD) of the numerator (18) and the denominator (30). The GCD of 18 and 30 is 6. Divide both the numerator and the denominator by the GCD:
18 ÷ 6 = 3 30 ÷ 6 = 5
This simplifies the fraction to 3/5.
-
Convert to a Decimal: Divide the numerator by the denominator:
3 ÷ 5 = 0.6
-
Convert to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.6 x 100 = 60%
Therefore, 18/30 simplifies to 3/5 and is equivalent to 60%.
Method 2: Direct Conversion to Percentage
This method involves converting the fraction directly to a percentage without simplifying first.
-
Convert to a Decimal: Divide the numerator by the denominator:
18 ÷ 30 = 0.6
-
Convert to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.6 x 100 = 60%
This method yields the same result: 60%. While seemingly quicker, simplifying first often leads to easier calculations, especially with larger numbers.
Understanding the Significance of 60%
60% represents a significant proportion. It's more than half (50%) but less than two-thirds (approximately 66.7%). Understanding this relative value is crucial for interpreting data and making informed decisions. For example, if a student answered 18 out of 30 questions correctly on a test, they achieved a score of 60%, indicating a satisfactory but not exceptional performance.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages has numerous practical applications in various fields:
- Finance: Calculating interest rates, discounts, profits, and losses.
- Statistics: Interpreting data, analyzing trends, and making predictions.
- Science: Expressing experimental results, calculating concentrations, and analyzing data.
- Everyday Life: Calculating tips, sales tax, and understanding proportions in recipes.
Expanding the Understanding: Further Exploration of Fractions and Percentages
Let's delve deeper into related concepts to enhance your understanding:
-
Percentage Increase and Decrease: Calculating the percentage change between two values is a common application. For example, if a price increases from $100 to $120, the percentage increase is calculated as follows:
((120 - 100) / 100) x 100% = 20%
-
Finding the Percentage of a Number: To find a certain percentage of a number, convert the percentage to a decimal and multiply it by the number. For instance, to find 60% of 250:
0.6 x 250 = 150
-
Working Backwards from a Percentage: If you know the percentage and the total, you can find the original value. For example, if 60% of a number is 150, the original number is:
150 / 0.6 = 250
Frequently Asked Questions (FAQ)
-
Q: Is there only one way to convert a fraction to a percentage?
A: No, there are several methods. The most efficient method often depends on the specific fraction and your comfort level with different calculation techniques.
-
Q: Why is simplifying a fraction important before converting to a percentage?
A: Simplifying makes the subsequent division and multiplication easier, reducing the chance of errors and making the calculations more manageable.
-
Q: What if the fraction results in a repeating decimal?
A: Some fractions, when converted to decimals, result in repeating decimals (e.g., 1/3 = 0.333...). In such cases, you can round the decimal to a reasonable number of places before converting it to a percentage.
-
Q: How can I improve my skills in converting fractions to percentages?
A: Practice is key! Try converting different fractions to percentages, using both methods described above. Start with simple fractions and gradually progress to more complex ones. Use online resources and practice problems to enhance your understanding.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental skill with broad applications. Understanding the underlying principles, employing efficient methods, and practicing regularly will significantly improve your mathematical proficiency. This guide has explored the conversion of 18/30 to 60% in detail, providing a step-by-step approach and addressing common questions. By mastering this skill, you'll be better equipped to tackle various mathematical challenges in both academic and real-world settings. Remember that consistent practice is the key to mastering this essential mathematical concept. Keep practicing, and you'll soon find yourself confidently navigating the world of fractions and percentages!
Latest Posts
Latest Posts
-
110 Km In Miles
Sep 17, 2025
-
Definition For Balanced Force
Sep 17, 2025
-
205 Minutes To Hours
Sep 17, 2025
-
63 2 Kg To Pounds
Sep 17, 2025
-
4 24 Equivalent Fractions
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 18/30 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.