2 1/2 As Decimal
renascent
Sep 23, 2025 · 6 min read
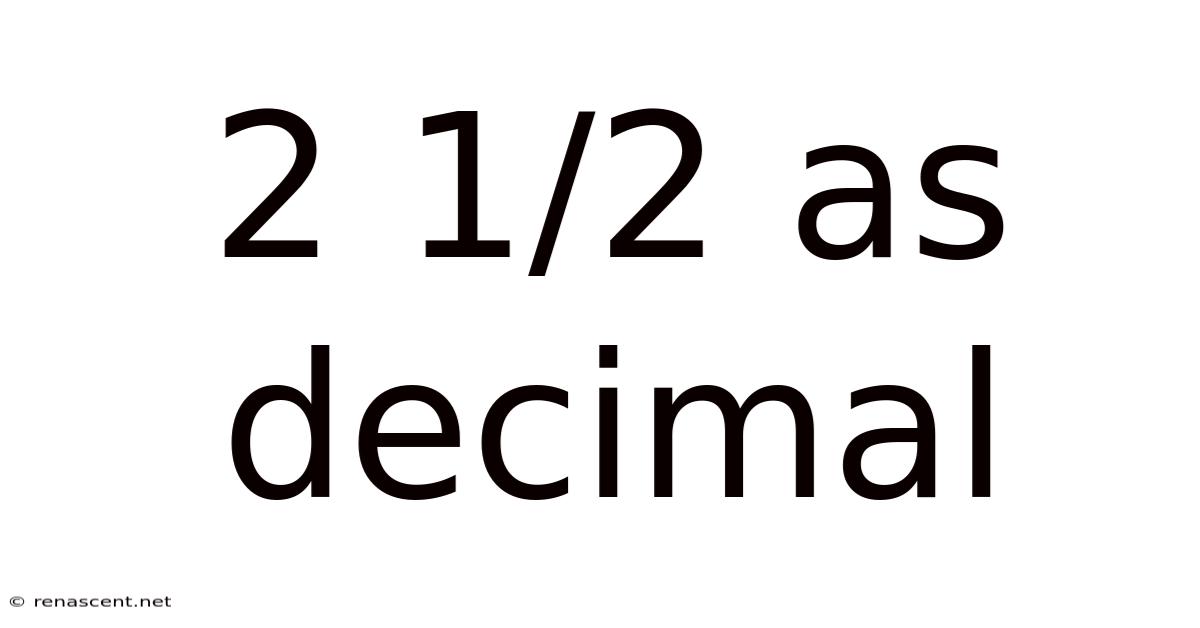
Table of Contents
Understanding 2 1/2 as a Decimal: A Comprehensive Guide
Mixed numbers, like 2 1/2, are a common part of everyday math. Understanding how to convert them into decimals is crucial for various applications, from calculating prices to solving complex equations. This comprehensive guide will walk you through the process of converting 2 1/2 to a decimal, explaining the underlying principles and providing additional examples to solidify your understanding. We'll explore different methods, delve into the mathematical concepts involved, and even address some frequently asked questions. By the end, you'll not only know the decimal equivalent of 2 1/2 but also possess a broader understanding of fraction-to-decimal conversions.
Understanding Mixed Numbers and Fractions
Before we dive into the conversion, let's briefly review the fundamentals. A mixed number combines a whole number and a fraction, like 2 1/2. The whole number (2) represents complete units, while the fraction (1/2) represents a part of a unit. A fraction, in its simplest form, represents a part of a whole. The number on top is called the numerator (1 in this case), and the number on the bottom is called the denominator (2 in this case). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have.
A decimal is a number expressed in base-10, using a decimal point to separate the whole number part from the fractional part. For instance, 2.5 is a decimal representing two whole units and five-tenths of a unit.
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This is arguably the most straightforward method for converting a mixed number like 2 1/2 into a decimal. We'll break it down into two steps:
Step 1: Convert the Fraction to a Decimal
To convert the fraction 1/2 to a decimal, we perform a simple division: divide the numerator (1) by the denominator (2).
1 ÷ 2 = 0.5
Step 2: Add the Whole Number
Now, we add the whole number part of the mixed number (2) to the decimal equivalent of the fraction (0.5):
2 + 0.5 = 2.5
Therefore, 2 1/2 as a decimal is 2.5.
Method 2: Converting the Mixed Number to an Improper Fraction, then to a Decimal
This method involves an intermediate step of converting the mixed number into an improper fraction before converting it to a decimal. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
Step 1: Convert the Mixed Number to an Improper Fraction
To convert 2 1/2 to an improper fraction, we multiply the whole number (2) by the denominator (2), add the numerator (1), and keep the same denominator (2):
(2 × 2) + 1 = 5
The improper fraction is 5/2.
Step 2: Convert the Improper Fraction to a Decimal
Now, we divide the numerator (5) by the denominator (2):
5 ÷ 2 = 2.5
Again, we arrive at the decimal equivalent of 2.5.
Method 3: Using Place Value Understanding
This approach relies on a deeper understanding of place value in the decimal system. We know that the place value immediately to the right of the decimal point represents tenths. The fraction 1/2 represents one-half, or five-tenths (5/10). Therefore, 2 1/2 can be directly written as 2.5.
Illustrative Examples: Extending the Concept
Let's apply these methods to a few more examples to reinforce your understanding:
Example 1: Converting 3 1/4 to a decimal
- Method 1: 1/4 = 0.25; 3 + 0.25 = 3.25
- Method 2: (3 × 4) + 1 = 13; 13/4 = 3.25
- Method 3: 1/4 is equivalent to 25/100 or 0.25. Therefore, 3 1/4 = 3.25
Example 2: Converting 1 3/5 to a decimal
- Method 1: 3/5 = 0.6; 1 + 0.6 = 1.6
- Method 2: (1 × 5) + 3 = 8; 8/5 = 1.6
- Method 3: 3/5 is equivalent to 6/10 or 0.6. Therefore, 1 3/5 = 1.6
Example 3: Converting 4 7/8 to a decimal
- Method 1: 7/8 = 0.875; 4 + 0.875 = 4.875
- Method 2: (4 × 8) + 7 = 39; 39/8 = 4.875
- Method 3: This requires understanding that 7/8 is 0.875. Therefore, 4 7/8 = 4.875
The Mathematical Principle Behind the Conversion
The core mathematical principle at play here is the relationship between fractions and decimals. Decimals are essentially fractions with denominators that are powers of 10 (10, 100, 1000, etc.). The conversion process involves expressing the fraction with a denominator that is a power of 10 or performing the division to find the decimal equivalent. For instance, 1/2 is easily converted to 5/10 or 0.5. More complex fractions may require long division or finding equivalent fractions with denominators that are powers of 10.
Frequently Asked Questions (FAQ)
Q1: What if the fraction doesn't easily convert to a decimal?
A1: Some fractions, such as 1/3 or 1/7, result in repeating decimals (0.333... and 0.142857142857...). In such cases, you can either express the decimal with a repeating bar notation (e.g., 0.3̅) or round the decimal to a certain number of decimal places for practical purposes.
Q2: Can I use a calculator to convert mixed numbers to decimals?
A2: Absolutely! Most calculators have the functionality to perform the division necessary for converting fractions to decimals. You can either convert the mixed number to an improper fraction first and then perform the division or divide the numerator by the denominator directly.
Q3: Are there any shortcuts for converting common fractions to decimals?
A3: Yes! Memorizing the decimal equivalents of common fractions like 1/2 (0.5), 1/4 (0.25), 1/5 (0.2), 1/8 (0.125), and 1/10 (0.1) can significantly speed up your calculations.
Q4: Why is understanding decimal conversion important?
A4: Decimal conversion is essential for various real-world applications, including:
- Financial calculations: Dealing with money often involves decimals.
- Measurements: Many measurements (length, weight, volume) use decimal systems.
- Scientific calculations: Decimals are widely used in scientific and engineering fields.
- Data analysis: Understanding decimals is crucial for interpreting data presented in decimal format.
Conclusion: Mastering Decimal Conversions
Converting mixed numbers, such as 2 1/2, to decimals is a fundamental skill in mathematics with widespread practical applications. By understanding the different methods outlined above – converting the fraction separately, converting to an improper fraction first, or using place value understanding – you can confidently tackle such conversions. Remember to practice regularly and utilize available resources like calculators to reinforce your understanding and improve your speed and accuracy. With enough practice, you'll master this essential mathematical concept and be well-equipped to handle more complex calculations involving fractions and decimals.
Latest Posts
Latest Posts
-
What Is Social Surplus
Sep 23, 2025
-
584 Calories To Kilojoules
Sep 23, 2025
-
200 G In Oz
Sep 23, 2025
-
10 Divided By 30
Sep 23, 2025
-
What Is Bill Exchange
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 1/2 As Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.