2 10 5 10
renascent
Sep 23, 2025 · 6 min read
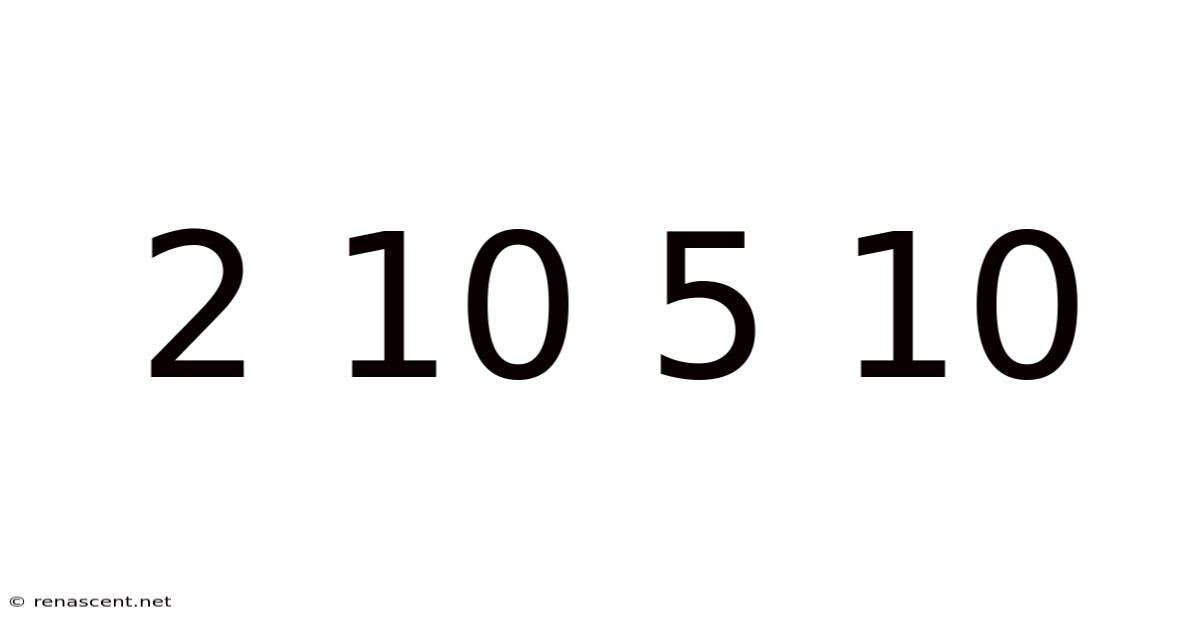
Table of Contents
Decoding the Sequence: Exploring the Mathematical and Logical Possibilities of "2 10 5 10"
The seemingly simple sequence "2 10 5 10" presents a fascinating challenge. At first glance, it might appear random. However, a deeper dive reveals a number of potential underlying patterns and mathematical relationships. This article will explore several interpretations of this sequence, examining different logical and mathematical approaches, and ultimately demonstrating how a seemingly straightforward puzzle can unveil a wealth of analytical possibilities. This exploration will cover various mathematical concepts and problem-solving strategies, making it suitable for anyone with a basic understanding of mathematics and a curiosity for puzzles.
Potential Interpretations and Patterns
The beauty of this sequence lies in its ambiguity. There's no single "correct" answer, but rather multiple plausible explanations depending on the assumptions and rules we apply. Let's explore some possibilities:
1. A Pattern Based on Simple Arithmetic Operations
One approach is to look for simple arithmetic relationships between consecutive numbers. Let's examine the differences and ratios:
-
Difference: The differences between consecutive numbers are 8, -5, and 5. This doesn't immediately reveal a clear pattern.
-
Ratio: The ratios are 5, 0.5, and 2. Again, no obvious pattern emerges.
However, we could consider more complex arithmetic operations. For instance, we could explore combinations of addition, subtraction, multiplication, and division. This would require a systematic approach, potentially testing various combinations until a consistent pattern is found.
2. A Pattern Based on Number Properties
We can also investigate the properties of the numbers themselves. Consider the following:
- Prime Factorization: The prime factorization of the numbers are:
- 2 = 2
- 10 = 2 x 5
- 5 = 5
- 10 = 2 x 5
This reveals a common factor of 2 and 5, suggesting a potential relationship. However, further analysis is needed to determine a concrete pattern.
- Odd and Even Numbers: The sequence alternates between even and odd numbers (2, 10, 5, 10). This could be a structural element of the pattern, but it doesn't provide a definitive solution on its own.
3. A Pattern Based on Geometric or Fibonacci-like Sequences
While the sequence doesn't directly follow a standard geometric or Fibonacci progression, we could explore modified versions of these sequences. For example:
-
Modified Geometric Sequence: A geometric sequence involves multiplying each term by a constant ratio. While the ratios in our sequence are inconsistent, it's possible to imagine a more complex pattern involving alternating ratios or a change in the ratio after a certain number of terms.
-
Modified Fibonacci Sequence: A Fibonacci sequence adds the two preceding terms to obtain the next term. This doesn't directly apply here, but we could explore a variation where, for example, we add or subtract specific numbers to the preceding terms to produce the next one. This could involve a combination of addition, subtraction, or other operations.
4. A Pattern Based on External References or Codes
It's possible that the sequence represents a code or refers to an external system. This would require additional context or information. For example:
-
Calendar Dates: Could the numbers represent days or months?
-
Measurement Units: Could they be related to specific units of measurement?
-
Codes or Ciphers: Could the sequence be part of a larger code or cipher that requires a key for decryption?
Without further information, this approach is largely speculative.
Advanced Mathematical Approaches
If simple arithmetic patterns prove elusive, we can explore more advanced mathematical techniques:
1. Polynomial Interpolation
Polynomial interpolation is a method used to find a polynomial function that passes through a given set of points. In this case, our points would be (1,2), (2,10), (3,5), (4,10). While this approach can find a polynomial that fits these points, it may not necessarily represent an underlying pattern or rule. The resulting polynomial might be complex and lack intuitive meaning.
2. Recurrence Relations
A recurrence relation defines a sequence recursively, meaning each term is defined based on the preceding terms. We could attempt to find a recurrence relation that generates our sequence. This would require solving a system of equations to determine the coefficients of the recurrence relation. However, due to the short length of the sequence, there might be multiple recurrence relations that could fit.
3. Generating Functions
Generating functions provide a powerful tool for analyzing sequences. A generating function represents a sequence as a power series. By manipulating this power series, we could potentially uncover hidden patterns or properties of the sequence. However, this approach would be more suitable for longer sequences or sequences with more apparent patterns.
Step-by-Step Problem-Solving Strategy
To systematically analyze the sequence "2 10 5 10", we can follow a structured approach:
-
Data Analysis: Start by examining the basic properties of the sequence – differences, ratios, prime factorization, odd/even numbers, etc.
-
Pattern Recognition: Look for obvious patterns based on arithmetic operations, geometric sequences, Fibonacci-like structures, or number properties.
-
Hypothesis Formulation: Based on the observations, formulate a hypothesis about the underlying pattern.
-
Hypothesis Testing: Test the hypothesis by applying it to the sequence. If it holds, try to extend the pattern to predict the next number(s) in the sequence.
-
Refinement: If the hypothesis doesn't hold, refine the hypothesis based on further observations and analysis. Iterate steps 3-5 until a plausible pattern is found.
-
Alternative Explanations: Consider alternative explanations, such as codes, external references, or more complex mathematical relationships.
-
Documentation: Keep detailed records of each step of the process, including hypotheses, calculations, and results. This helps to trace the steps and identify areas for improvement.
Frequently Asked Questions (FAQ)
Q: Is there a single correct answer to this sequence puzzle?
A: No, there isn't a single definitive answer. Multiple patterns and interpretations are possible depending on the assumptions and methods used. The solution depends on the context and the constraints applied.
Q: What are the limitations of applying simple arithmetic operations to solve this problem?
A: Simple arithmetic operations might fail to uncover complex patterns or relationships within the sequence. A more complex pattern could require more advanced mathematical techniques or require additional information or context.
Q: How can I improve my ability to solve these types of sequence puzzles?
A: Practice is key! Work through various sequence puzzles, exploring different techniques and strategies. Develop a systematic approach to problem-solving, and document your work carefully. The more familiar you become with different mathematical concepts and problem-solving methods, the easier these problems will become.
Conclusion
The sequence "2 10 5 10" serves as an excellent example of how a seemingly simple mathematical puzzle can unveil numerous possibilities. While there is no single "correct" answer, the process of exploring different patterns and applying various mathematical techniques enhances our problem-solving skills and reveals the rich interconnectedness of mathematical concepts. This exercise highlights the importance of a systematic approach, creative thinking, and persistence in tackling seemingly intractable problems. By exploring this sequence, we’ve not only examined specific patterns but also gained a broader appreciation for the diverse methods used in mathematical problem-solving, emphasizing the importance of careful analysis, hypothesis formulation, and testing in reaching a plausible conclusion. The inherent ambiguity of the sequence encourages a multifaceted approach, allowing us to delve into different mathematical realms and appreciate the beauty of mathematical exploration itself.
Latest Posts
Latest Posts
-
1 12 As A Decimal
Sep 23, 2025
-
Dr Catherine Harris Medicare
Sep 23, 2025
-
Histogram Or Bar Graph
Sep 23, 2025
-
Square Root Of 216
Sep 23, 2025
-
Gcf 15 And 25
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 10 5 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.