2 10 X 2
renascent
Sep 25, 2025 · 6 min read
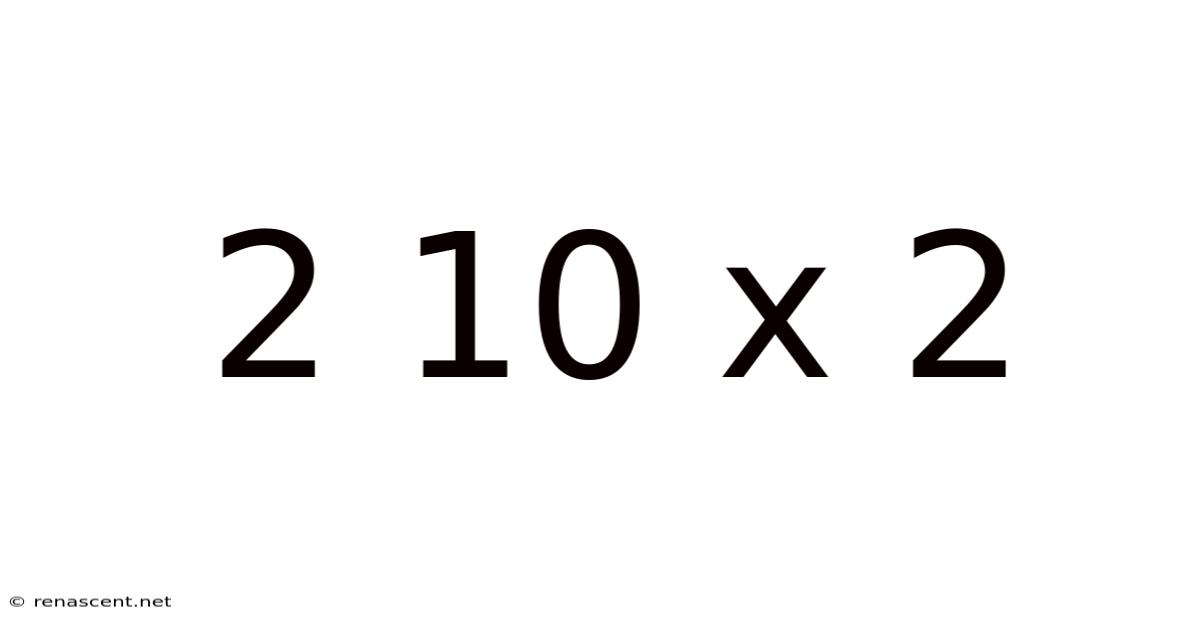
Table of Contents
Decoding 2 x 10 x 2: Exploring Multiplication, Area, and Volume
This article delves into the seemingly simple mathematical expression "2 x 10 x 2," exploring its various interpretations and applications across different areas of mathematics, particularly in calculating area and volume. We'll move beyond the basic arithmetic and delve into the underlying concepts, examining how this expression can represent real-world scenarios and providing a deeper understanding of its implications. This exploration will benefit students learning about basic arithmetic, area calculations, and volume calculations. We will cover everything from the fundamental principles of multiplication to practical examples.
Understanding the Fundamentals: Multiplication
At its core, "2 x 10 x 2" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that signifies repeated addition. In this instance, we are repeatedly adding the number 2, ten times, and then doubling the result. The order of operations doesn't matter in this case because multiplication is commutative (meaning the order of the numbers doesn't affect the outcome). Therefore, 2 x 10 x 2 is equivalent to 10 x 2 x 2, 2 x 2 x 10, and so on.
The calculation is straightforward:
- 2 x 10 = 20
- 20 x 2 = 40
Therefore, the answer to 2 x 10 x 2 is 40.
Application 1: Calculating Area
The expression "2 x 10 x 2" can be interpreted as a calculation of area, particularly when dealing with three-dimensional objects. Imagine a rectangular prism or box. Let's break it down:
-
2 x 10: This could represent the area of one face of the rectangular prism. For example, it could be a rectangle with a length of 10 units and a width of 2 units. The area of this rectangle is 20 square units (length x width).
-
2 x 10 x 2: Now, if the height of this rectangular prism is also 2 units, we're essentially calculating the volume, not just the area of one face. We'll cover volume in more detail in the next section. However, it's important to note that the expression, in itself, can represent the calculation of area if we consider a 2D context. Consider a scenario where we have two rectangular regions, both 10 units long and 2 units wide, placed side by side. The total area of this combined region will be 2 * (2 x 10) = 40 square units.
Application 2: Calculating Volume
"2 x 10 x 2" is most readily applied to the calculation of volume. This expression represents the volume of a rectangular prism (also called a cuboid). The dimensions are:
- Length: 10 units
- Width: 2 units
- Height: 2 units
The formula for the volume of a rectangular prism is: Volume = Length x Width x Height
Therefore, 2 x 10 x 2 represents a volume calculation:
- 2 (height) x 10 (length) x 2 (width) = 40 cubic units
This means the prism has a volume of 40 cubic units. This could represent 40 cubic centimeters, 40 cubic meters, or any other cubic unit, depending on the context of the problem.
Visualizing the Problem
Imagine building a rectangular structure using blocks. If each block represents one cubic unit, to build a structure with the dimensions 2 x 10 x 2, you would need 40 blocks. Visualizing the structure helps understand how the multiplication works in three dimensions. You would create a layer of 10 blocks (10 x 2), then stack another layer on top, giving you a total of 40 blocks (2 layers x 20 blocks per layer).
Real-World Applications
The concept of calculating volume using 2 x 10 x 2 has numerous real-world applications:
- Packaging and Shipping: Determining the volume of a box needed to ship a product.
- Construction: Calculating the amount of material needed to fill a space, such as concrete for a foundation.
- Aquariums: Determining the volume of water needed to fill a tank.
- Agriculture: Calculating the volume of soil needed for a planter box or raised bed garden.
Expanding the Concept: Exploring Different Dimensions
While we've focused on a rectangular prism, the principles of multiplication can be applied to calculate the volume of other shapes. Understanding the basic principle of "2 x 10 x 2" allows a deeper understanding of more complex volume calculations which use different equations. The fundamental idea remains the same: multiplying the relevant dimensions to obtain the total volume. The more complex shapes may require more advanced mathematical tools such as calculus or integral methods, but the underlying concept of using repeated multiplication to calculate volume remains crucial.
Beyond the Numbers: Understanding Units
It's crucial to emphasize the importance of units when dealing with area and volume calculations. "40" by itself is just a number. The complete answer must include units to provide context and meaning. If the dimensions are in centimeters, the volume is 40 cubic centimeters (cm³). If the dimensions are in meters, the volume is 40 cubic meters (m³). Understanding units is essential for accurate communication and problem-solving in real-world applications.
Frequently Asked Questions (FAQ)
Q: What if the order of the numbers is changed? Does it affect the result?
A: No. Multiplication is commutative, meaning the order of the numbers doesn't affect the product. 2 x 10 x 2 is equal to 10 x 2 x 2, 2 x 2 x 10, and so on. The result will always be 40.
Q: Can this expression represent something other than area and volume?
A: While area and volume are the most common applications, it could represent other scenarios involving repeated multiplication. For example, it could represent the number of items arranged in a specific arrangement. Imagine 2 stacks of 10 items, each stack having 2 distinct types of items. This would total 40 items. The context is crucial in interpreting the meaning.
Q: How does this relate to more complex mathematical concepts?
A: This simple expression lays the foundation for understanding more complex mathematical concepts such as algebra, calculus, and even linear algebra. It helps develop the ability to visualize multi-dimensional spaces and perform calculations that are essential for solving more complex problems in various fields like physics and engineering.
Q: What are some common mistakes students make when calculating volume?
A: A common mistake is forgetting to cube the units (using cm² instead of cm³ for cubic centimeters). Another is misinterpreting the dimensions or applying the wrong formula. Careful attention to detail and a clear understanding of the formula are essential to avoid errors.
Conclusion: A Simple Expression, Endless Possibilities
The seemingly simple mathematical expression "2 x 10 x 2" offers a rich opportunity to explore fundamental mathematical concepts such as multiplication, area, and volume. By understanding its application in various contexts, students can develop a deeper appreciation for the importance of these concepts in real-world scenarios. The ability to visualize the problem and correctly apply the relevant formula is crucial for achieving accuracy in calculations. Moving forward, this fundamental understanding will prove invaluable as they progress to more advanced mathematical concepts. Remember to always pay close attention to the units used in measurements to ensure accurate and meaningful results. This simple equation opens doors to a deeper understanding of the mathematical world and its practical applications.
Latest Posts
Latest Posts
-
Kadalai Maavu In English
Sep 25, 2025
-
1 L To Qt
Sep 25, 2025
-
Pt To Ml Converter
Sep 25, 2025
-
16 20 In Percent
Sep 25, 2025
-
Ethanoic Acid Sodium Carbonate
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 2 10 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.