2 3 7 9
renascent
Sep 18, 2025 · 5 min read
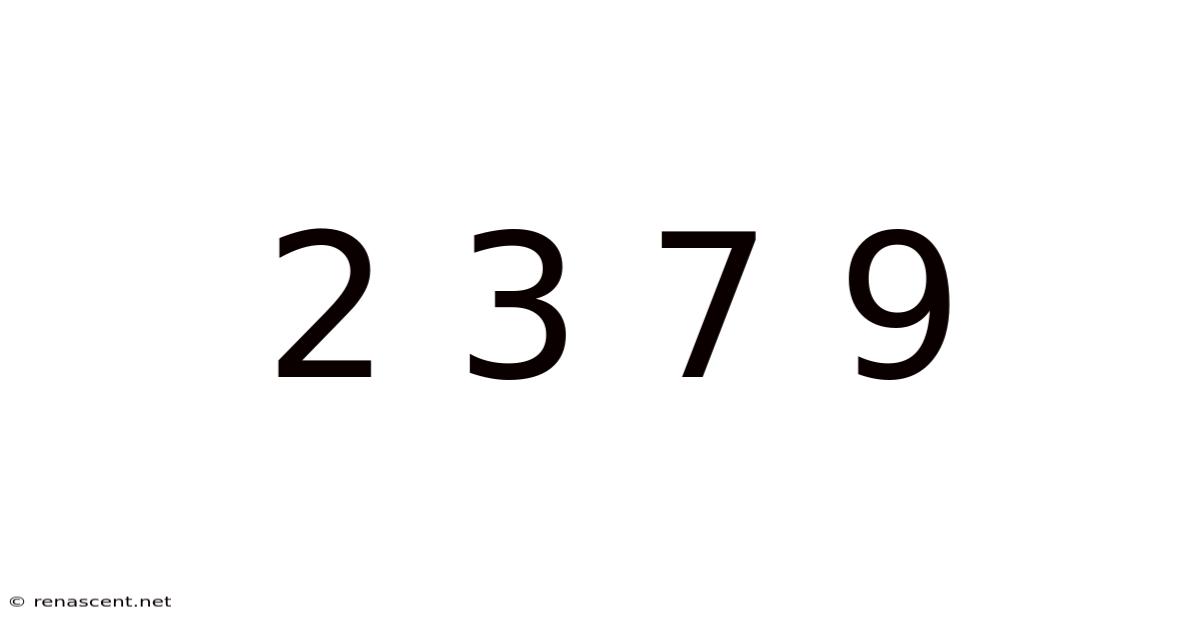
Table of Contents
Unlocking the Mysteries: Exploring the Mathematical Significance and Patterns within the Sequence 2, 3, 7, 9
The seemingly simple sequence of numbers, 2, 3, 7, 9, might at first glance appear random. However, a deeper dive into the world of mathematics reveals that this sequence, while short, offers a fertile ground for exploring various mathematical concepts, patterns, and potential extensions. This article will delve into different interpretations and perspectives on this sequence, examining its properties from the viewpoints of number theory, sequence analysis, and even creative problem-solving. We will uncover potential underlying patterns, discuss possible generalizations, and address frequently asked questions.
Understanding the Sequence: Initial Observations
Before venturing into complex analysis, it’s crucial to establish a baseline understanding of the sequence 2, 3, 7, 9. Initially, no immediately obvious arithmetic or geometric progression is apparent. The differences between consecutive numbers (1, 4, 2) are not consistent. This lack of a straightforward pattern suggests we need to explore more sophisticated mathematical tools and perspectives to unlock the hidden structure.
Exploring Potential Patterns and Relationships
One approach to understanding this sequence is to investigate potential relationships between the numbers. Let's explore some possibilities:
-
Prime Numbers: Notice that 2, 3, and 7 are all prime numbers (numbers divisible only by 1 and themselves). 9, however, is a composite number (9 = 3 x 3). This observation partially explains the lack of a simple arithmetic progression but might suggest a relationship with prime numbers and their squares.
-
Modulo Operations: Analyzing the sequence modulo various integers can reveal hidden patterns. For instance, considering the sequence modulo 2, we get 0, 1, 1, 1. Modulo 3, we have 2, 0, 1, 0. While these don't immediately reveal clear patterns, they demonstrate a method for exploring underlying structures.
-
Differences and Second Differences: Calculating the differences between consecutive terms, and then the differences between those differences (second differences), is a common technique in sequence analysis. As mentioned earlier, the first differences (1, 4, 2) are irregular. The second differences (-3, -2) are also irregular, suggesting a non-quadratic relationship.
Generating Functions and Recursive Relationships
A more advanced approach involves constructing a generating function for the sequence. A generating function is a formal power series where the coefficients correspond to the terms of the sequence. While it's challenging to derive a simple, closed-form generating function for this specific sequence, exploring this avenue opens possibilities for representing the sequence in a more concise and potentially revealing way.
Another avenue is exploring recursive relationships. A recursive relationship defines a term in the sequence based on previous terms. Again, finding a simple recursive relationship for this sequence is not straightforward. This lack of a readily apparent recursive formula highlights the sequence's complexity and lack of an easily identifiable pattern.
Expanding the Sequence: Hypothetical Extensions
Given the lack of a clearly defined pattern, the question of how to extend this sequence becomes a matter of speculation and hypothesis. Several approaches could be considered:
-
Prime Number Focus: If we hypothesize that the sequence is related to prime numbers, we might extend it by including the next prime numbers (11, 13, 17, 19...). This approach, however, neglects the inclusion of 9, which is not prime.
-
Modulo-Based Extension: Building upon the modulo analysis, we could try to identify a consistent modulo pattern and use it to predict subsequent terms. However, the irregularity of the modulo results for different moduli makes this approach challenging and unreliable for creating a consistent extension.
-
Polynomial Approximation: We could attempt to fit a polynomial function to the given data points (assuming the sequence represents a discrete function). This approach might provide an approximate extension, but the accuracy of the approximation would depend on the degree of the polynomial and might not reflect the underlying (if any) true mathematical relationship.
The Significance of Context and Problem Definition
The difficulty in identifying a definitive pattern within the sequence 2, 3, 7, 9 highlights the importance of context and a well-defined problem statement. If this sequence emerged from a specific mathematical problem, riddle, or puzzle, the solution might lie in understanding the context within which the sequence was generated. Without this context, the numerous possibilities for interpretation and extension make it impossible to define a unique, universally accepted continuation of the sequence.
Frequently Asked Questions (FAQs)
Q1: Is there a definitive mathematical formula for this sequence?
A1: No, there's no universally accepted, simple mathematical formula or closed-form expression that perfectly generates this sequence. The lack of readily apparent arithmetic or geometric progression, as well as the absence of a simple recursive relationship, suggests the sequence's nature is more complex and potentially context-dependent.
Q2: Can this sequence be extended uniquely?
A2: No. Without a clearly defined generating mechanism or pattern, extending the sequence uniquely is impossible. Multiple plausible extensions can be proposed based on different interpretations and assumptions about the sequence's underlying structure.
Q3: What mathematical concepts are relevant to analyzing this sequence?
A3: Several mathematical concepts are relevant, including number theory (prime numbers, divisibility), sequence analysis (differences, generating functions, recursive relationships), and polynomial approximation. The analysis also showcases the importance of context and problem definition in mathematical problem-solving.
Q4: What if the sequence were longer? Would that help?
A4: A longer sequence might reveal more subtle patterns or relationships that are currently obscured by the limited number of terms. However, even with a longer sequence, there's no guarantee of finding a simple, universally accepted mathematical formula or recursive relationship.
Conclusion: The Enduring Mystery of 2, 3, 7, 9
The sequence 2, 3, 7, 9, despite its brevity, presents a fascinating case study in mathematical exploration. It demonstrates that not all numerical sequences adhere to straightforward patterns. The lack of an easily identifiable formula or recursive relationship underscores the importance of considering various mathematical techniques and the crucial role of context in mathematical problem-solving. While we haven't found a definitive answer, the process of investigating this sequence illustrates the beauty and challenges inherent in unraveling the mysteries of numbers and their patterns. The quest to understand this simple-looking sequence opens doors to a deeper appreciation of the power and limitations of various mathematical tools and the importance of creative thinking in exploring the unknown. Further exploration might involve investigating more advanced mathematical concepts and employing computational methods to explore potential patterns and relationships within larger datasets inspired by this initial sequence. The journey of discovery continues.
Latest Posts
Latest Posts
-
Mark And Release Method
Sep 18, 2025
-
24 Percent Of 30
Sep 18, 2025
-
As Sharp As Simile
Sep 18, 2025
-
150 Seconds To Minutes
Sep 18, 2025
-
What Is 30 5
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 3 7 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.