2/3 Divided By 2
renascent
Sep 22, 2025 · 6 min read
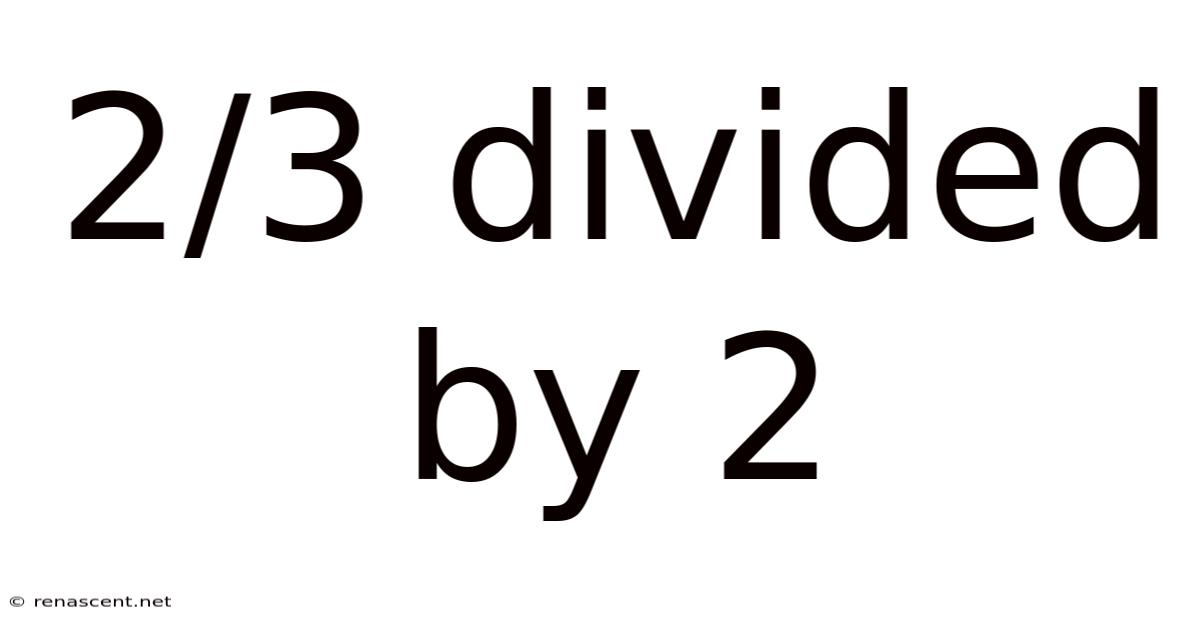
Table of Contents
2/3 Divided by 2: A Deep Dive into Fraction Division
Understanding fraction division can be tricky, but it's a fundamental skill in mathematics with applications across various fields. This comprehensive guide will walk you through the process of dividing the fraction 2/3 by 2, explaining the underlying principles and providing multiple approaches to solve this problem. We'll explore various methods, address common misconceptions, and delve into the practical implications of such calculations. By the end of this article, you'll not only know the answer but also confidently tackle similar fraction division problems.
Understanding Fraction Division: The Basics
Before we tackle 2/3 divided by 2, let's refresh our understanding of fraction division. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. This principle is crucial for solving any fraction division problem.
In essence, when you divide a fraction by a whole number, you're essentially dividing the numerator (the top number) by that whole number. However, understanding the reciprocal method offers a more robust and versatile approach, especially when dealing with more complex fractions.
Method 1: Dividing the Numerator Directly
The simplest approach to solving 2/3 divided by 2 involves directly dividing the numerator by the divisor. Remember, the whole number 2 can be written as a fraction: 2/1. Therefore, our problem becomes (2/3) ÷ (2/1).
To solve this, we can apply the rule of dividing fractions: keep the first fraction (2/3), change the division sign to multiplication, and flip the second fraction (2/1 becomes 1/2). This gives us:
(2/3) x (1/2) = (2 x 1) / (3 x 2) = 2/6
We can then simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
2/6 = 1/3
Therefore, 2/3 divided by 2 equals 1/3.
Method 2: Using the Reciprocal Method
This method reinforces the understanding of reciprocals and offers a more generalized approach applicable to various fraction division problems. Again, we start with (2/3) ÷ 2. We rewrite 2 as 2/1.
Now, we apply the reciprocal rule:
(2/3) ÷ (2/1) = (2/3) x (1/2)
Multiply the numerators together and the denominators together:
(2 x 1) / (3 x 2) = 2/6
Simplify the resulting fraction:
2/6 = 1/3
This confirms our earlier result: 2/3 divided by 2 equals 1/3.
Visualizing Fraction Division
Understanding fraction division can be significantly enhanced through visualization. Imagine you have a chocolate bar divided into three equal pieces (representing 2/3). Now, you want to divide these two-thirds into two equal shares. You would split each of the two existing pieces in half, resulting in four smaller pieces. You would then take one of the two pieces from the original two-thirds of the chocolate bar. This visual representation shows that you end up with 2 out of 6 pieces, or 1/3 of the original chocolate bar.
Understanding the Concept of Reciprocal
The concept of the reciprocal is central to understanding fraction division. The reciprocal, or multiplicative inverse, of a number is the number that, when multiplied by the original number, equals 1. For example, the reciprocal of 2/3 is 3/2 because (2/3) x (3/2) = 1.
Understanding reciprocals allows us to convert a division problem into a multiplication problem, which is often easier to solve. This is particularly helpful when dealing with more complex fractions.
Addressing Common Misconceptions
A frequent mistake is to divide both the numerator and the denominator by the divisor. While this works for some operations, it's incorrect in fraction division. You are dividing the entire fraction by the divisor, not just its parts. Incorrectly dividing both the numerator and the denominator by 2 in this case would yield (2/2)/(3/2) = 1/(3/2), leading to the wrong answer. Always remember the steps of converting the division into multiplication by using the reciprocal.
Extending the Concept: More Complex Problems
The methods outlined above can be extended to solve more complex fraction division problems. For instance, consider the problem (5/8) ÷ (3/4).
-
Rewrite: The problem becomes (5/8) x (4/3).
-
Multiply: Multiply the numerators and the denominators: (5 x 4) / (8 x 3) = 20/24.
-
Simplify: Simplify the fraction by finding the greatest common divisor (GCD) of 20 and 24, which is 4. Dividing both by 4 gives us 5/6.
Therefore, (5/8) ÷ (3/4) = 5/6. This demonstrates the versatility of the reciprocal method in solving more challenging fraction division problems.
Practical Applications of Fraction Division
Fraction division is not merely an abstract mathematical concept; it has many practical applications in daily life and various professional fields.
-
Cooking & Baking: Dividing recipes to adjust serving sizes frequently involves fraction division. If a recipe calls for 2/3 cup of flour, and you want to make half the recipe, you would need to divide 2/3 by 2 to determine the amount of flour needed.
-
Construction & Engineering: Precise measurements in construction and engineering often involve fractions. Dividing materials or lengths requires understanding fraction division.
-
Finance: Calculating proportions of investments or splitting costs often involves fractions and their division.
-
Data Analysis: Working with datasets that involve fractions or proportions necessitates understanding fraction division for accurate calculations and interpretations.
Frequently Asked Questions (FAQ)
Q1: Can I divide the numerator and denominator separately when dividing a fraction by a whole number?
A1: No. This method only works for multiplying or dividing fractions by the same number, but it does not apply to dividing a fraction by a whole number. Always use the reciprocal method or the direct numerator division method explained above.
Q2: What if I get a mixed number as a result of the division?
A2: If you obtain a mixed number, you can convert it to an improper fraction for simplification and further calculations.
Q3: What happens if I divide by a fraction instead of a whole number?
A3: The process remains the same. You still change the division sign to multiplication and use the reciprocal of the fraction you are dividing by.
Q4: How can I improve my understanding of fraction division?
A4: Practice regularly with various problems. Visual aids like diagrams or real-world examples can greatly help in grasping the concept.
Conclusion: Mastering Fraction Division
Dividing fractions, including the seemingly simple problem of 2/3 divided by 2, is a crucial skill in mathematics. This article has explored multiple methods, addressed common misconceptions, and highlighted the practical applications of this skill. By understanding the reciprocal method and applying the steps consistently, you can confidently tackle fraction division problems of varying complexity. Remember, consistent practice and a solid understanding of fundamental principles are key to mastering this essential mathematical skill. Through practice and the techniques explained, you can build your confidence and competence in working with fractions. Remember that mastering mathematics is a journey, not a sprint, and each step you take toward understanding these fundamental concepts is a step closer to achieving greater mathematical fluency.
Latest Posts
Latest Posts
-
Molecular Mass Of Cl2
Sep 22, 2025
-
Mg To Milliliters Calculator
Sep 22, 2025
-
Blue Eyed Dark Hair
Sep 22, 2025
-
1 8 In Decimals
Sep 22, 2025
-
150 Mins In Hours
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.