2/5 Divided By 5
renascent
Sep 23, 2025 · 6 min read
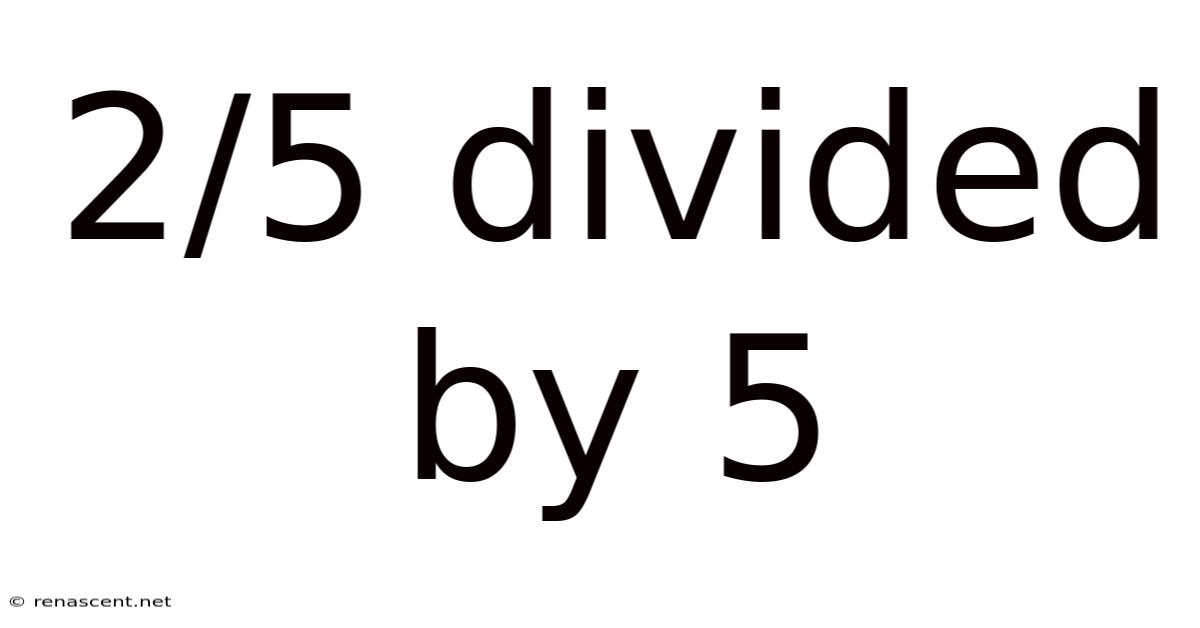
Table of Contents
Decoding 2/5 Divided by 5: A Deep Dive into Fraction Division
Understanding fraction division can feel daunting, but with the right approach, it becomes surprisingly straightforward. This article will dissect the problem of 2/5 divided by 5, guiding you through the process step-by-step and exploring the underlying mathematical principles. We'll cover various methods, offering a comprehensive understanding suitable for students and anyone looking to refresh their fraction skills. By the end, you'll not only know the answer to 2/5 divided by 5 but also possess a strong foundation for tackling similar problems confidently.
Introduction: Why Fraction Division Matters
Fractions are fundamental to mathematics and appear frequently in everyday life, from cooking and construction to finance and data analysis. Mastering fraction operations, especially division, is crucial for navigating these real-world scenarios. This article focuses on the seemingly simple problem of 2/5 divided by 5, but the principles we explore apply to a wide range of fraction division problems. We'll demystify the process, showing you that fraction division isn't as intimidating as it might first appear.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is arguably the most popular method for dividing fractions. It’s efficient and easy to remember. The steps are as follows:
- Keep: Keep the first fraction exactly as it is. In our case, this remains 2/5.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (find the reciprocal of) the second fraction. The reciprocal of 5 (which can be written as 5/1) is 1/5.
Therefore, the problem 2/5 ÷ 5 transforms into:
2/5 × 1/5
- Multiply: Now, multiply the numerators (top numbers) together and the denominators (bottom numbers) together.
(2 × 1) / (5 × 5) = 2/25
Therefore, 2/5 divided by 5 is equal to 2/25.
Method 2: Converting to a Decimal
Another approach involves converting the fractions into decimals before performing the division. This method is particularly helpful when using a calculator.
- Convert the fraction to a decimal: 2/5 is equivalent to 0.4 (because 2 ÷ 5 = 0.4).
- Perform decimal division: Now, divide the decimal by 5: 0.4 ÷ 5 = 0.08
Therefore, 2/5 divided by 5 is equal to 0.08. Note that 0.08 is the decimal representation of 2/25. This demonstrates the equivalence of the two methods.
Method 3: Visual Representation with Area Models
Visualizing the problem can enhance understanding, especially for beginners. Imagine a rectangle representing a whole unit. Divide this rectangle into five equal parts. Two of these five parts represent 2/5.
Now, imagine dividing these 2/5 into five equal groups. Each group will represent a smaller fraction of the whole. Each of the original five sections is now further subdivided into five smaller sections. This results in a total of 25 smaller sections.
Two of the original five sections are shaded (representing 2/5). If we split those two shaded sections into five equal smaller parts each, we'll have 10 smaller sections shaded. But we only want to show one-fifth of the original shaded sections. So we look at only two of the ten smaller shaded sections. Those two sections represent 2 out of the 25 smaller sections. Therefore, the resulting fraction is 2/25. This visual approach reinforces the result obtained through the other methods.
Method 4: Understanding the Concept of Division
Division fundamentally asks "how many times does one number go into another?" When dividing fractions, we're asking how many times 5 goes into 2/5. Since 5 is larger than 2/5, the answer will be a fraction less than 1.
The "Keep, Change, Flip" method essentially rephrases this question. Instead of asking "how many times does 5 go into 2/5?", we are asking "what fraction of 5 is needed to get 2/5?" This is where the reciprocal comes in; flipping the 5/1 to 1/5 gives us the fraction of 5 that results in 2/5. Multiplying these then gives the correct answer.
Explanation with Scientific Notation and Significant Figures:
While not strictly necessary for this simple problem, let's briefly touch upon how this would be handled with scientific notation and significant figures, which is important in scientific and engineering contexts.
2/5 can be expressed as 0.4 or 4 x 10⁻¹. Dividing this by 5 gives us 8 x 10⁻². This is equivalent to 0.08. In this simple case, both the initial fraction and the final answer have only one significant figure (as 2 and 5 can be considered exact numbers).
Frequently Asked Questions (FAQ)
-
Q: Can I divide fractions using a calculator? A: Yes, most calculators can handle fraction division. You might need to use the fraction function (often represented as a/b) or convert the fractions to decimals before division.
-
Q: Why does the "Keep, Change, Flip" method work? A: This method is a shortcut derived from the rules of fraction multiplication and reciprocals. Dividing by a number is the same as multiplying by its reciprocal.
-
Q: What if the second number is also a fraction? A: The "Keep, Change, Flip" method works perfectly well even if both numbers are fractions. You would simply keep the first fraction, change the division to multiplication, and flip the second fraction before multiplying.
-
Q: Are there other methods for dividing fractions? A: While the methods discussed here are the most common and efficient, other methods exist, often involving finding a common denominator and then dividing the numerators. These methods are generally less efficient than the "Keep, Change, Flip" method.
-
Q: How do I check my answer? A: You can verify your answer by multiplying the result (2/25) by the divisor (5). The result should be the original dividend (2/5).
Conclusion: Mastering Fraction Division
Dividing fractions might seem intimidating initially, but with practice and a clear understanding of the underlying principles, it becomes a manageable skill. The "Keep, Change, Flip" method provides a simple and efficient way to tackle these problems. Remember to always check your answer to ensure accuracy. The more you practice, the more comfortable you will become with fraction division and its various applications in math and beyond. This comprehensive guide, coupled with regular practice, will equip you with the necessary tools to confidently approach any fraction division problem. By understanding the different methods, the underlying principles, and by answering common questions, you gain a strong command of this essential mathematical skill. Remember that mathematics is built upon a foundation of understanding and practice; by mastering this concept, you're not just solving a single problem, but building a stronger mathematical foundation for future learning.
Latest Posts
Latest Posts
-
Gluten Free Slider Buns
Sep 23, 2025
-
Electrons In Carbon Atom
Sep 23, 2025
-
30 Out Of 32
Sep 23, 2025
-
Model Lock And Key
Sep 23, 2025
-
Electron Configuration For Mg
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2/5 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.