2 9 As Percent
renascent
Sep 17, 2025 · 5 min read
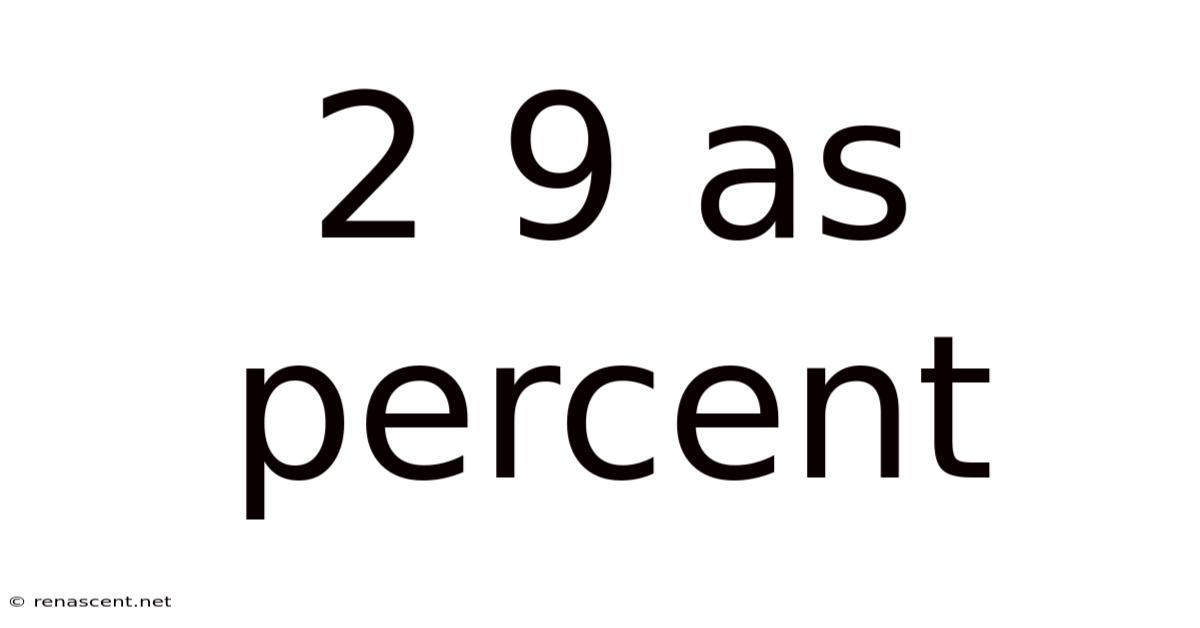
Table of Contents
Decoding 2/9 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, with applications spanning various fields from finance to science. This article provides a comprehensive guide on how to convert the fraction 2/9 into a percentage, explaining the process step-by-step and exploring related concepts. We will delve into the methodology, offer practical examples, and address frequently asked questions to ensure a thorough understanding of this crucial mathematical concept. This guide is designed for students, professionals, and anyone seeking a clearer grasp of percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion of 2/9 to a percentage, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 2/9, 2 is the numerator and 9 is the denominator. This means we are considering 2 parts out of a total of 9 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion relative to a whole, where the whole is considered as 100%. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100 and then expressing this as a percentage.
Converting 2/9 to a Percentage: Step-by-Step
There are several ways to convert the fraction 2/9 into a percentage. Let's explore the most common and straightforward methods:
Method 1: Direct Conversion using Division
-
Divide the numerator by the denominator: Divide 2 by 9. This gives us 0.2222... (a repeating decimal).
-
Multiply the result by 100: Multiply 0.2222... by 100. This gives us 22.222...
-
Express the result as a percentage: The result, 22.222..., is expressed as 22.22%. Since the decimal is repeating, we typically round to a suitable number of decimal places, depending on the context of the problem. In many cases, rounding to two decimal places (22.22%) is sufficient.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding a number that, when multiplied by 9 (the denominator), results in 100. However, this isn't directly possible since 9 doesn't divide evenly into 100. Therefore, we use the decimal approach as outlined in Method 1. We can, however, use this method to conceptualize the problem: Imagine dividing a whole into 9 equal parts. If you take 2 of these parts, what percentage of the whole do you have? The answer will be approximately 22.22%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply input 2/9 and then use the percentage function or multiply the result by 100. The calculator will directly display the percentage equivalent.
Understanding the Repeating Decimal
The conversion of 2/9 results in a repeating decimal (0.222...). This is because 9 is a factor of 10 (10 = 2 x 5), but not of 100 (100 = 2^2 x 5^2). The repeating nature of the decimal emphasizes the fact that 2/9 is a rational number that cannot be precisely represented as a finite decimal. The repeating decimal 0.222... is often written as 0.2̅ to indicate that the digit 2 repeats infinitely.
Practical Applications and Examples
The ability to convert fractions to percentages is vital in many real-world situations:
-
Calculating Discounts: A store offers a 2/9 discount on an item. To determine the exact percentage discount, we convert 2/9 to a percentage (approximately 22.22%).
-
Analyzing Data: In statistical analysis, representing data as percentages often provides a clearer and more intuitive understanding than using fractions. For instance, if 2 out of 9 students passed an exam, this could be represented as approximately 22.22% pass rate.
-
Financial Calculations: Percentage calculations are fundamental in finance, used for calculating interest rates, returns on investments, and profit margins.
-
Scientific Research: Percentages are widely used in scientific research to express proportions, ratios, and experimental results.
Further Exploration: Understanding Ratios and Proportions
The concept of 2/9 as a percentage is closely related to ratios and proportions. A ratio is a comparison of two quantities. The ratio 2:9 represents the same relationship as the fraction 2/9. A proportion is a statement that two ratios are equal. Understanding ratios and proportions can deepen your understanding of percentage calculations.
Frequently Asked Questions (FAQ)
Q: Why does 2/9 result in a repeating decimal when converted to a percentage?
A: The repeating decimal arises because the denominator (9) does not divide evenly into 100. When converting fractions to decimals, a repeating decimal occurs when the denominator contains prime factors other than 2 and 5.
Q: Is it always necessary to round the percentage?
A: Depending on the context, rounding may be necessary for practical purposes. In some cases, expressing the exact repeating decimal (22.222...) might be preferred for higher accuracy.
Q: Can I use a different method to convert 2/9 to a percentage?
A: While the methods described above are common, other approaches using more advanced mathematical concepts might exist, but they would likely be more complex for this specific example.
Q: How do I convert other fractions to percentages?
A: The same principles apply to other fractions. Divide the numerator by the denominator and multiply the result by 100.
Q: What if I have a mixed number, not just a simple fraction?
A: Convert the mixed number to an improper fraction first, and then follow the same process as described above.
Conclusion
Converting 2/9 to a percentage involves a straightforward process, primarily involving division and multiplication. Understanding the steps involved and the underlying mathematical concepts is crucial for applying this skill in various contexts. Whether you are a student mastering fundamental mathematical concepts or a professional utilizing percentages in your work, this comprehensive guide provides a solid foundation for understanding and confidently applying percentage conversions. Remember to always consider the level of precision needed for your specific application when rounding repeating decimals.
Latest Posts
Latest Posts
-
3 Of 1 Million
Sep 18, 2025
-
3 5 Gallons In Litres
Sep 18, 2025
-
76 F In C
Sep 18, 2025
-
55 Gallons To Litres
Sep 18, 2025
-
2 7 To Percent
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 9 As Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.