2 Percent Of 8
renascent
Sep 23, 2025 · 5 min read
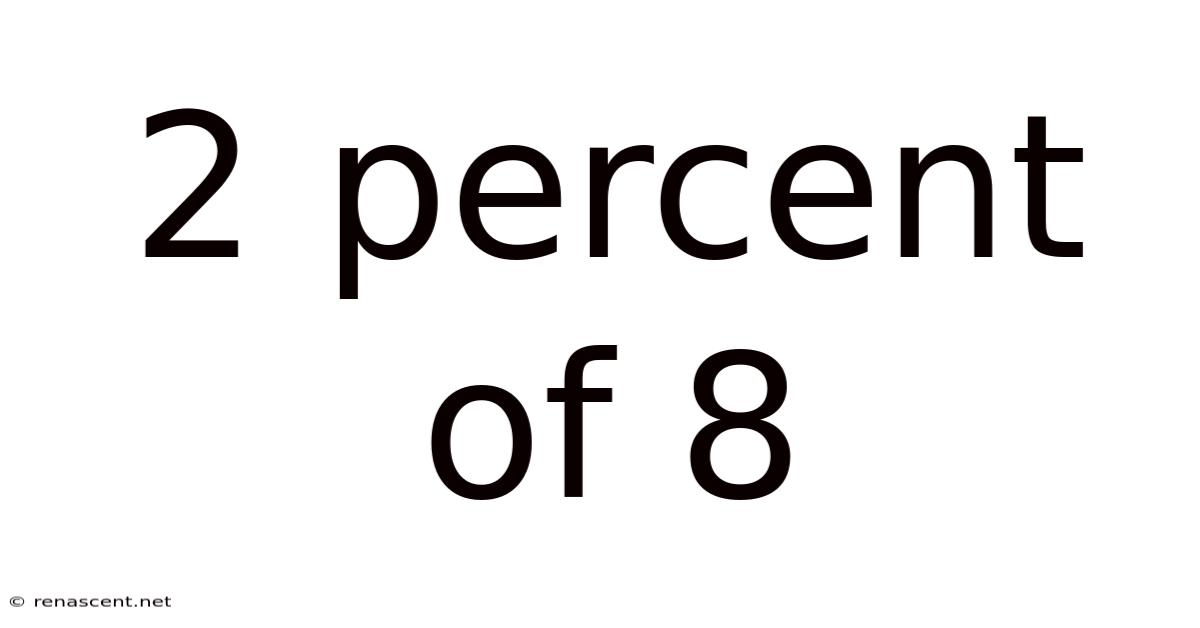
Table of Contents
Decoding 2 Percent of 8: A Deep Dive into Percentages and Their Applications
Finding 2 percent of 8 might seem like a simple calculation, a task easily handled by a calculator. However, understanding the underlying principles of percentages is crucial for numerous applications in everyday life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will not only solve the problem of "2 percent of 8" but will also explore the broader concept of percentages, demonstrating their importance and providing various methods for calculating them. We'll delve into the mathematical foundations, explore real-world examples, and address frequently asked questions to ensure a comprehensive understanding of this fundamental mathematical concept.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 2 percent (written as 2%) means 2 out of every 100. This can be represented as a fraction (2/100) or as a decimal (0.02). Understanding these different representations is key to performing percentage calculations efficiently.
The core concept revolves around the relationship between a part, a whole, and the percentage representing the part's proportion relative to the whole. In the case of "2 percent of 8," 8 represents the whole, and we need to find the part that constitutes 2% of this whole.
Method 1: Using the Fraction Method
This is arguably the most intuitive method, especially for those who prefer a more visual approach. We convert the percentage into a fraction and then multiply it by the whole number.
-
Step 1: Convert the percentage to a fraction. 2% can be written as 2/100.
-
Step 2: Simplify the fraction (if possible). 2/100 simplifies to 1/50.
-
Step 3: Multiply the fraction by the whole number. (1/50) * 8 = 8/50
-
Step 4: Simplify the resulting fraction (if possible). 8/50 simplifies to 4/25
-
Step 5: Convert the fraction to a decimal (optional). 4/25 = 0.16
Therefore, 2 percent of 8 is 0.16 or 4/25.
Method 2: Using the Decimal Method
This method uses the decimal equivalent of the percentage. It's often faster for those comfortable with decimal calculations.
-
Step 1: Convert the percentage to a decimal. 2% is equal to 0.02 (move the decimal point two places to the left).
-
Step 2: Multiply the decimal by the whole number. 0.02 * 8 = 0.16
This method directly gives us the answer in decimal form: 0.16.
Method 3: Using Proportions
This method employs the concept of ratios and proportions, providing a more algebraic approach to solving percentage problems.
-
Step 1: Set up a proportion. We can express the problem as a proportion: x/8 = 2/100, where 'x' represents the unknown value (2% of 8).
-
Step 2: Cross-multiply. 100x = 16
-
Step 3: Solve for x. x = 16/100 = 0.16
This method confirms that 2 percent of 8 is 0.16.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in a wide variety of real-world scenarios. Here are just a few examples:
-
Sales and Discounts: Calculating discounts offered during sales events. For example, a 20% discount on a $50 item.
-
Taxes: Determining the amount of sales tax or income tax payable.
-
Interest Rates: Calculating simple and compound interest on loans and investments.
-
Tips and Gratuities: Calculating appropriate tips in restaurants or for service providers.
-
Statistics and Data Analysis: Interpreting statistical data, such as percentages representing market share, population growth, or survey results.
-
Financial Reports: Understanding financial statements, analyzing profit margins, and assessing investment performance.
-
Cooking and Baking: Scaling recipes up or down based on percentage increases or decreases of ingredients.
Beyond the Basics: More Complex Percentage Problems
While finding 2% of 8 is a straightforward calculation, many real-world applications involve more complex percentage problems. These often involve:
-
Finding the Percentage: Determining what percentage one number is of another. For example, what percentage is 5 of 20? (Answer: 25%)
-
Finding the Original Value: Calculating the original value before a percentage increase or decrease. For example, if a price increased by 10% to $110, what was the original price? (Answer: $100)
-
Consecutive Percentages: Applying multiple percentages successively. For example, a 10% increase followed by a 5% decrease.
These more advanced problems require a deeper understanding of percentage principles and often involve a multi-step approach.
Frequently Asked Questions (FAQ)
Q: Why are percentages important?
A: Percentages provide a standardized way to express proportions and ratios, making it easier to compare and analyze data across different contexts. They are essential for making informed decisions in various aspects of life, from personal finance to professional applications.
Q: What is the difference between percentage and fraction?
A: A percentage is a specific type of fraction where the denominator is always 100. A fraction can have any denominator. Percentages are generally used for expressing proportions in a more readily understandable format.
Q: How can I improve my skills in calculating percentages?
A: Practice is key! Start with simple problems and gradually work towards more complex ones. Familiarize yourself with different methods of calculation (fraction, decimal, proportion) and choose the method you find most comfortable and efficient. Use online resources, worksheets, and real-world examples to reinforce your understanding.
Q: Are there any online tools to help with percentage calculations?
A: While this article avoids external links, many websites and apps offer percentage calculators. These can be useful for checking your answers and gaining additional practice. Many scientific and standard calculators also have built-in percentage functions.
Q: Can percentages be greater than 100%?
A: Yes, percentages can be greater than 100%. This represents a quantity that is more than the whole. For example, a 150% increase means the quantity has increased by 1.5 times its original value.
Conclusion
Calculating 2 percent of 8, while seemingly trivial, serves as a gateway to understanding the broader concept of percentages. The ability to perform percentage calculations is a fundamental skill applicable across diverse fields. Mastering this skill involves not only knowing the different calculation methods but also appreciating their relevance in various real-world situations. By understanding the underlying principles and practicing different approaches, you can confidently tackle percentage problems of increasing complexity and apply this knowledge effectively in your daily life and professional endeavors. From managing personal finances to interpreting complex data sets, a solid grasp of percentages empowers you to make informed decisions and navigate a numerically driven world with confidence.
Latest Posts
Latest Posts
-
1 9 2 0
Sep 23, 2025
-
Happy Anniversary In French
Sep 23, 2025
-
Basin Of Holy Water
Sep 23, 2025
-
13 16 As A Percentage
Sep 23, 2025
-
Maclaurin Series For Cosx
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.