2 X 2 1
renascent
Sep 15, 2025 · 5 min read
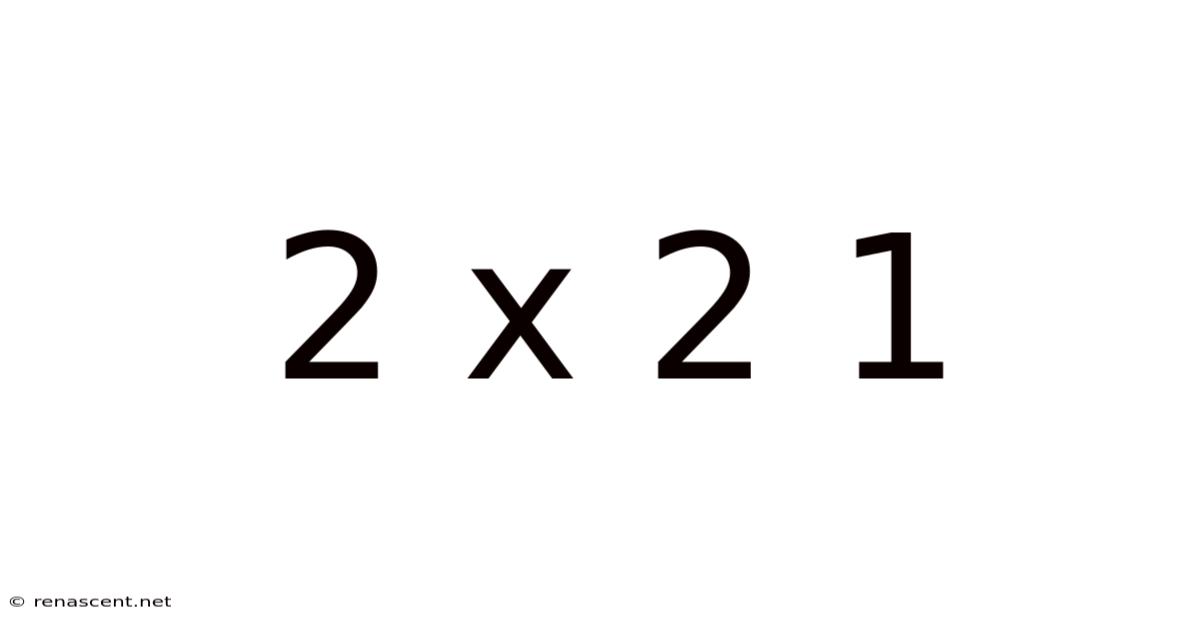
Table of Contents
Decoding the Enigma: A Deep Dive into 2 x 2 = 1 (and Why it's Not True in Standard Arithmetic)
The seemingly simple equation, 2 x 2 = 1, immediately strikes us as incorrect. In standard arithmetic, the answer is unequivocally 4. However, understanding why this seemingly false statement holds no merit in our conventional mathematical framework opens the door to explore fascinating concepts in abstract algebra, modular arithmetic, and the limitations of assuming a single, universal system. This article will delve into the intricacies of this equation, exploring its potential meanings within specific contexts and highlighting why it’s crucial to understand the underlying mathematical structures.
Introduction: The World Beyond Standard Arithmetic
Our initial reaction to 2 x 2 = 1 is a justifiable sense of disbelief. We’re taught from a young age that multiplication represents repeated addition. Two groups of two objects undeniably equal four objects. But mathematics extends far beyond the familiar realm of elementary arithmetic. The statement 2 x 2 = 1 can be true, but only within specific, well-defined mathematical systems, not within the realm of real numbers.
Exploring Modular Arithmetic: A System of Remainders
One area where a similar result can appear is in modular arithmetic. Modular arithmetic deals with remainders after division. We denote this as "modulo," often abbreviated as "mod." For example, 7 mod 3 = 1 because when 7 is divided by 3, the remainder is 1. Let’s consider a modulo 3 system.
-
In modulo 3:
- 2 + 2 = 4 ≡ 1 (mod 3)
- 2 x 2 = 4 ≡ 1 (mod 3)
In this system, the numbers "wrap around" after reaching a certain point (in this case, 3). Therefore, 4 is equivalent to 1 (mod 3). This does not mean 4 equals 1 in the traditional sense; it simply means they have the same remainder when divided by 3. This is a crucial distinction.
Group Theory: A Framework of Abstract Algebra
Group theory, a branch of abstract algebra, provides a more sophisticated perspective. Groups are sets of elements with a defined operation that satisfies specific axioms (rules). These axioms ensure the operation behaves in a predictable way. One crucial axiom is the existence of an identity element – an element that, when operated on another element, leaves that element unchanged. In standard multiplication, the identity element is 1 (any number multiplied by 1 remains the same).
Let’s imagine a simplified group with only two elements, {0, 1}. We can define a multiplication operation in a non-standard way:
- 0 x 0 = 0
- 0 x 1 = 0
- 1 x 0 = 0
- 1 x 1 = 1
Notice that under this system, 1 acts as an identity element. However, this system doesn't resemble standard arithmetic. In this specific group structure, the equation 2 x 2 = 1 simply doesn't make sense because the numbers 2 are not part of the group's defined elements.
Boolean Algebra and Logical Operations
Boolean algebra, named after George Boole, deals with binary values, typically represented as 0 (false) and 1 (true). In this system, operations are defined using logical AND, OR, and NOT. While not directly related to the equation 2 x 2 = 1 in a numerical sense, the concept of a binary system sheds light on how seemingly unconventional results can arise within specific contexts. In Boolean algebra, the operators operate differently than in standard arithmetic, making direct numerical comparison meaningless.
The Importance of Context and Defining Operations
The core takeaway is that the meaning of an equation, such as 2 x 2 = 1, is entirely dependent on the context in which it's presented and the operations defined within that context. In standard arithmetic over real numbers, this equation is unequivocally false. However, within specific algebraic structures or modular arithmetic systems, a similar result might be obtained due to the specific rules and definitions of those systems.
Frequently Asked Questions (FAQ)
Q: Can 2 x 2 ever truly equal 1?
A: No, in standard arithmetic using real numbers, 2 x 2 will always equal 4. The equation 2 x 2 = 1 can only be true within specific mathematical systems with non-standard definitions of multiplication or within modular arithmetic where the result refers to a remainder rather than an absolute value.
Q: What are some real-world applications of modular arithmetic?
A: Modular arithmetic has numerous real-world applications, including:
- Cryptography: Encryption and decryption algorithms heavily rely on modular arithmetic to ensure data security.
- Computer Science: Hashing functions and checksums use modular arithmetic to detect errors in data transmission and storage.
- Calendar Systems: Determining the day of the week for a given date often involves modular arithmetic.
- Music Theory: Musical scales and intervals can be represented using modular arithmetic.
Q: Is this equation a mathematical trick or a fallacy?
A: It's not a trick or fallacy in the sense of being deliberately deceptive. It's a demonstration of how different mathematical systems operate under different rules. It highlights the importance of understanding the underlying mathematical framework before attempting to interpret equations or results.
Q: Are there other examples of unexpected results in different mathematical systems?
A: Yes, many! Consider the concept of infinity in calculus. Different types of infinity can have unexpected relationships with each other, leading to counterintuitive results. The study of complex numbers also introduces properties and operations that aren't present in real numbers.
Conclusion: Expanding Mathematical Horizons
The seemingly simple equation, 2 x 2 = 1, serves as a powerful reminder that mathematics extends far beyond the basic arithmetic we learn in school. By exploring modular arithmetic and abstract algebra, we glimpse the rich tapestry of mathematical systems, each with its own unique rules and properties. Understanding these different systems enhances our appreciation for the flexibility and power of mathematics, reminding us that seemingly contradictory results can arise when working within different mathematical frameworks. The equation serves not as a falsehood, but as a gateway to broader mathematical concepts and the crucial role of context in interpreting mathematical statements. While 2 x 2 will always equal 4 in our everyday arithmetic, exploring the exceptions and nuances broadens our understanding and appreciation of the vast and fascinating field of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.