20/25 As A Percentage
renascent
Sep 16, 2025 · 6 min read
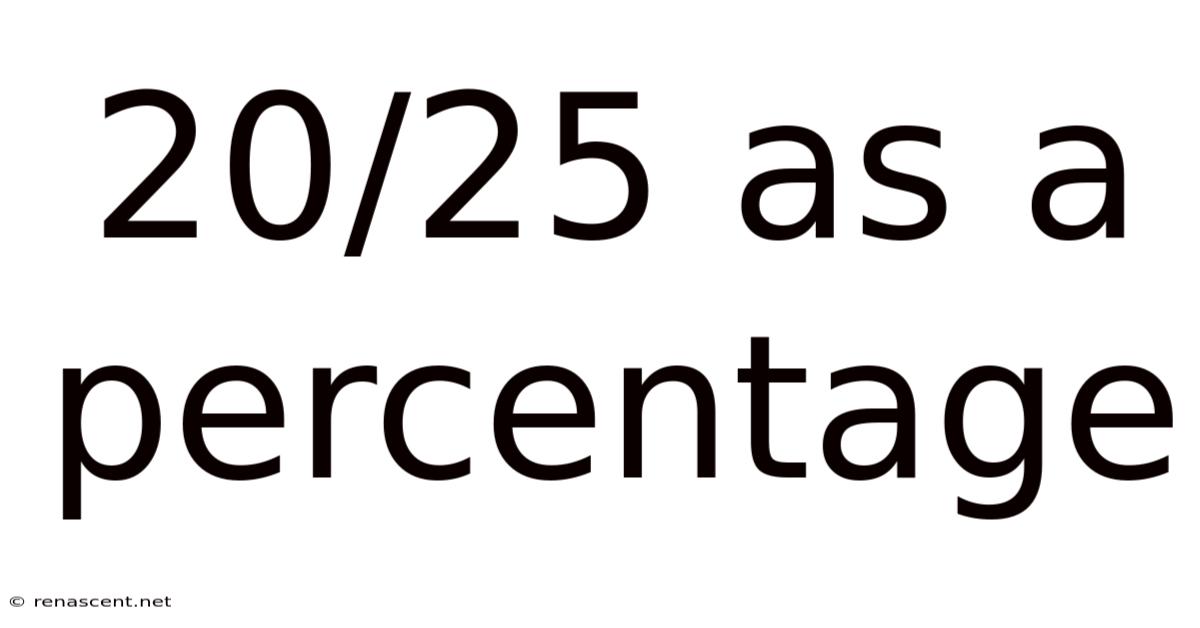
Table of Contents
Understanding 20/25 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across various fields, from calculating grades to understanding financial data. This article provides a comprehensive guide to understanding how to convert the fraction 20/25 into a percentage, explaining the process step-by-step and exploring related concepts. We'll delve into the underlying principles, offer practical examples, and address frequently asked questions, ensuring a thorough understanding for learners of all levels. This guide will equip you with the knowledge to confidently tackle similar fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion of 20/25, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 20/25, 20 is the numerator and 25 is the denominator.
A percentage is a way of expressing a number as a fraction of 100. The symbol % represents "per cent," meaning "out of 100." Percentages are widely used to express proportions, rates, and changes. For example, 80% means 80 out of 100, or 80/100.
Converting 20/25 to a Percentage: Method 1 - Direct Conversion
The most straightforward way to convert 20/25 to a percentage is to first convert the fraction to an equivalent fraction with a denominator of 100. Since 25 multiplied by 4 equals 100, we can multiply both the numerator and the denominator of 20/25 by 4:
(20 x 4) / (25 x 4) = 80/100
Since 80/100 means 80 out of 100, this is equivalent to 80%.
Therefore, 20/25 is equal to 80%.
Converting 20/25 to a Percentage: Method 2 - Decimal Conversion
Another common method involves first converting the fraction to a decimal and then converting the decimal to a percentage.
To convert 20/25 to a decimal, we divide the numerator (20) by the denominator (25):
20 ÷ 25 = 0.8
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage sign (%):
0.8 x 100 = 80
Therefore, 0.8 is equal to 80%.
This confirms that 20/25 is indeed equal to 80%.
Simplifying Fractions Before Conversion
Before performing either of the above methods, it's often helpful to simplify the fraction to its lowest terms. This simplifies the calculations and makes the conversion process easier. In this case, both 20 and 25 are divisible by 5:
20 ÷ 5 = 4 25 ÷ 5 = 5
This simplifies the fraction to 4/5. Now we can use either method:
Method 1 (Direct Conversion):
To convert 4/5 to a percentage with a denominator of 100, we multiply both the numerator and the denominator by 20:
(4 x 20) / (5 x 20) = 80/100 = 80%
Method 2 (Decimal Conversion):
To convert 4/5 to a decimal, we divide 4 by 5:
4 ÷ 5 = 0.8
Then, we multiply the decimal by 100:
0.8 x 100 = 80%
Again, we arrive at the same answer: 80%. Simplifying the fraction first often makes the calculation smoother and less prone to errors.
Real-World Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in many real-world scenarios. Here are a few examples:
- Academic Performance: If a student answers 20 out of 25 questions correctly on a test, their score is 80%.
- Sales and Discounts: A store offering a 20% discount on an item priced at $25 is effectively reducing the price by $5 (20% of $25).
- Financial Calculations: Calculating interest rates, profit margins, and tax percentages all require converting fractions to percentages.
- Data Analysis: Representing data visually using charts and graphs often involves converting fractions or ratios into percentages for easier interpretation.
- Surveys and Polls: Results from surveys and polls are frequently presented as percentages to show the proportion of respondents who chose a particular option.
Further Exploration: Understanding Percentage Increase and Decrease
The conversion of 20/25 to 80% can be further understood in the context of percentage increase and decrease. Let's say you started with a quantity of 25 and increased it by 20 units. You can express this change as a percentage increase.
- Original Quantity: 25
- Increase: 20
- New Quantity: 45
The percentage increase is calculated as: (Increase / Original Quantity) x 100% = (20 / 25) x 100% = 80%
This means the quantity increased by 80%. Conversely, if you started with 45 and decreased it by 20 units, you would end up with 25, representing an 80% decrease from 45. This demonstrates the interconnectedness of percentage increase, decrease, and the underlying fractional representation.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert 20/25 to a percentage?
A1: Yes, absolutely! Most calculators have a percentage function. You can either divide 20 by 25 and then multiply the result by 100, or use the fraction function directly to convert 20/25 to a decimal and then to a percentage.
Q2: What if the fraction doesn't easily convert to a denominator of 100?
A2: If the denominator isn't a simple factor of 100, you can still use the decimal conversion method. Divide the numerator by the denominator to obtain the decimal equivalent, and then multiply by 100 to get the percentage. For example, converting 7/13 to a percentage involves dividing 7 by 13 (approximately 0.538) and then multiplying by 100 (approximately 53.8%).
Q3: Is there a difference between 20/25 and 80%?
A3: No, there is no mathematical difference. 20/25 and 80% represent the same proportion or quantity. They are simply different ways of expressing the same value. The choice of which to use depends on context and clarity. Percentages are generally preferred for ease of understanding and comparison in many situations.
Q4: How can I improve my understanding of fraction-to-percentage conversions?
A4: Practice is key! Try converting different fractions to percentages using both methods. Start with simple fractions and gradually work your way up to more complex ones. Online resources, worksheets, and practice problems can provide ample opportunities to improve your skills. Understanding the fundamental concepts of fractions and decimals is essential for mastering percentage conversions.
Conclusion
Converting fractions to percentages is a vital mathematical skill with broad applications. This article has demonstrated two effective methods for converting 20/25 to a percentage, highlighting the equivalence between 20/25 and 80%. We explored the underlying principles of fractions and percentages, discussed the advantages of simplifying fractions before conversion, and illustrated the relevance of percentage conversions in various real-world situations. By mastering this skill, you'll improve your ability to interpret data, analyze information, and solve problems across various academic and professional fields. Remember to practice regularly to enhance your understanding and build confidence in tackling similar calculations.
Latest Posts
Latest Posts
-
163 Pounds To Kilos
Sep 16, 2025
-
390 Minutes To Hours
Sep 16, 2025
-
Demonic Wisp Blox Fruits
Sep 16, 2025
-
2000 Pounds In Kilograms
Sep 16, 2025
-
238 Pounds To Kg
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 20/25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.