20 Percent Of 25
renascent
Sep 21, 2025 · 5 min read
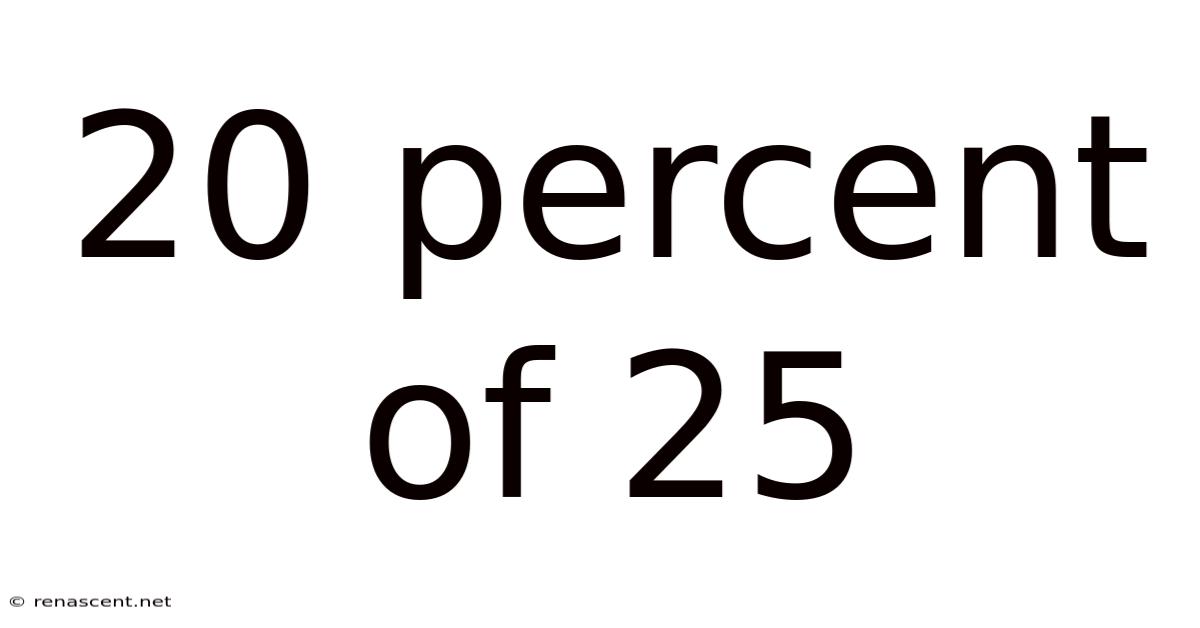
Table of Contents
Calculating 20% of 25: A Deep Dive into Percentages and Their Applications
Finding 20% of 25 might seem like a simple calculation, easily solved with a calculator. However, understanding the underlying principles of percentages is crucial for numerous applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This article will not only show you how to calculate 20% of 25 but will also explore the broader context of percentages, different methods of calculation, and real-world examples. This comprehensive guide aims to provide a solid foundation in percentage calculations, making you confident in tackling similar problems in the future.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" (from Latin per centum). Therefore, 20% means 20 out of 100, which can be represented as a fraction (20/100) or a decimal (0.20). Understanding this fundamental concept is key to solving percentage problems.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method for calculating percentages. We convert the percentage to its decimal equivalent and then multiply it by the number.
Steps:
-
Convert the percentage to a decimal: To convert 20% to a decimal, divide it by 100: 20% ÷ 100 = 0.20
-
Multiply the decimal by the number: Multiply the decimal equivalent (0.20) by the number you want to find the percentage of (25): 0.20 x 25 = 5
Therefore, 20% of 25 is 5.
Method 2: Using Fractions
Percentages can also be expressed as fractions. This method offers a deeper understanding of the underlying mathematical principles.
Steps:
-
Express the percentage as a fraction: 20% can be written as 20/100.
-
Simplify the fraction (if possible): 20/100 simplifies to 1/5 by dividing both the numerator and denominator by 20.
-
Multiply the fraction by the number: Multiply the simplified fraction (1/5) by 25: (1/5) x 25 = 5
Therefore, 20% of 25 is 5. This method clearly demonstrates that finding 20% of 25 is equivalent to finding one-fifth of 25.
Method 3: Using Proportions
The proportion method is a more formal approach, particularly useful for solving more complex percentage problems.
Steps:
-
Set up a proportion: We can set up a proportion as follows:
20/100 = x/25
Where 'x' represents the unknown value (20% of 25).
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa:
20 x 25 = 100x
-
Solve for x: Divide both sides by 100:
500 = 100x x = 500/100 = 5
Therefore, 20% of 25 is 5. This method highlights the relationship between the percentage, the whole number, and the part representing the percentage.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for navigating numerous real-world scenarios. Here are some examples:
-
Discounts: Retail stores frequently offer discounts. If a $25 item is discounted by 20%, you would save $5 (20% of 25).
-
Sales Tax: Sales tax is added to the price of goods and services. If the sales tax is 6% and you buy a $25 item, you will pay an additional $1.50 (6% of 25).
-
Tips: When dining out, it's customary to tip the server. A 20% tip on a $25 meal would be $5.
-
Interest Rates: Interest rates are percentages that determine the cost of borrowing money or the return on investment. Understanding interest calculations is fundamental to personal finance.
-
Commission: Sales representatives often earn a commission, a percentage of their sales. If a salesperson earns a 10% commission on a $250 sale, they earn $25 (10% of 250).
-
Statistical Data: Percentages are frequently used to represent data in graphs, charts, and reports. For example, understanding that 20% of respondents chose a particular option in a survey is a key piece of information.
Calculating Other Percentages of 25
Let's expand our understanding by calculating other percentages of 25 using the decimal method:
- 10% of 25: 0.10 x 25 = 2.5
- 50% of 25: 0.50 x 25 = 12.5
- 75% of 25: 0.75 x 25 = 18.75
- 100% of 25: 1.00 x 25 = 25
- 15% of 25: 0.15 x 25 = 3.75
More Complex Percentage Problems
While 20% of 25 is a relatively simple calculation, the principles extend to more complex problems. For example, you might need to calculate the percentage increase or decrease between two numbers or determine the original price after a percentage discount has been applied. These problems often require a multi-step approach, employing the methods discussed above.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The decimal method is generally considered the easiest and most efficient way, especially for simple calculations. Convert the percentage to a decimal (by dividing by 100) and multiply it by the number.
Q: Can I use a calculator for percentage calculations?
A: Absolutely! Calculators are invaluable tools for percentage calculations, especially for more complex problems or those involving larger numbers. Most calculators have a percentage button (%) which simplifies the process.
Q: How do I calculate the percentage one number represents of another?
A: To find what percentage one number is of another, divide the first number by the second number and then multiply by 100. For example, to find what percentage 5 is of 25: (5/25) x 100 = 20%.
Q: What if I need to calculate a percentage increase or decrease?
A: For percentage increase: (New Value - Original Value) / Original Value x 100%. For percentage decrease: (Original Value - New Value) / Original Value x 100%.
Conclusion
Calculating 20% of 25, while seemingly straightforward, provides a gateway to understanding the broader world of percentage calculations. Mastering these calculations equips you with essential skills applicable in diverse fields, from personal finance and shopping to interpreting statistical data and solving more complex mathematical problems. Remember the three methods explained – using decimals, fractions, and proportions – each offers a different perspective and can be adapted to various scenarios. The key is to grasp the fundamental concept of percentages as ratios out of 100, and practice applying these methods to different problems. With consistent practice, you will become confident and proficient in tackling any percentage-related challenge.
Latest Posts
Latest Posts
-
Australia Longitude And Latitude
Sep 22, 2025
-
Hydrogen Gas Pop Test
Sep 22, 2025
-
Quotes From Hedda Gabler
Sep 22, 2025
-
1 2 Of 57
Sep 22, 2025
-
Street Names For Cocaine
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.