20 Percent Of 3000
renascent
Sep 14, 2025 · 5 min read
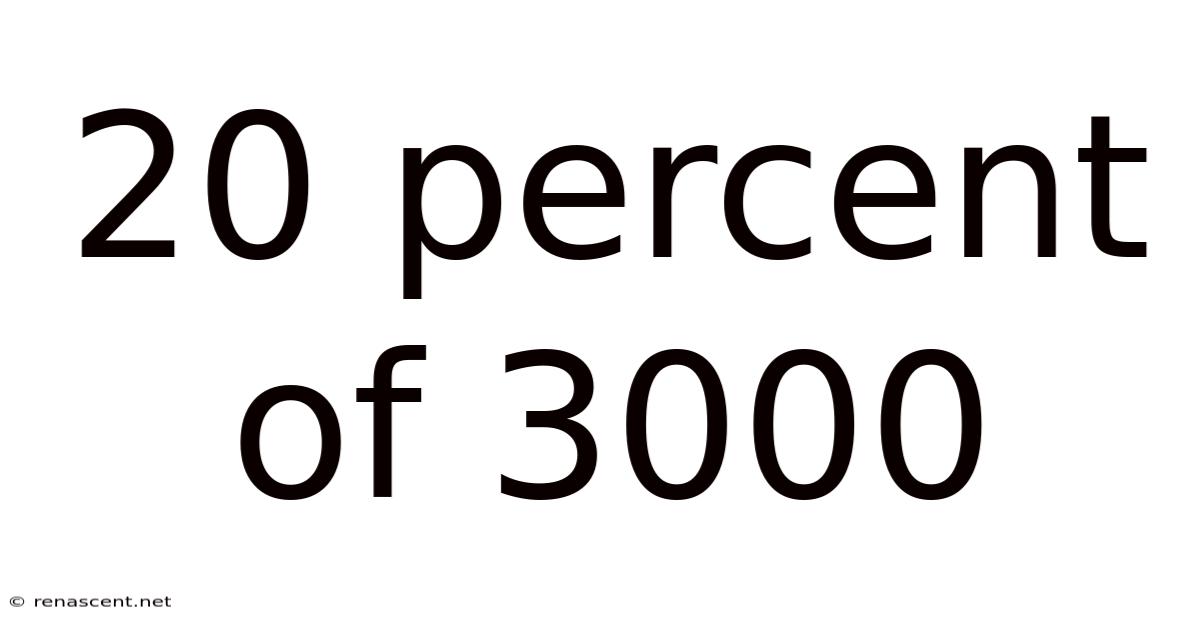
Table of Contents
Decoding 20% of 3000: A Deep Dive into Percentages and Their Applications
Finding 20% of 3000 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to calculate percentages and their real-world applications is a crucial skill applicable across numerous fields, from budgeting and finance to scientific analysis and data interpretation. This article will not only show you how to calculate 20% of 3000 but also explore the underlying concepts, different calculation methods, and various practical examples to solidify your understanding of percentages.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin phrase "per centum," meaning "out of one hundred." Therefore, 20% literally means 20 out of 100, or 20/100, which simplifies to 1/5. This fundamental understanding is key to grasping percentage calculations.
Calculating 20% of 3000: Three Methods
There are several ways to calculate 20% of 3000. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent by dividing the percentage by 100. 20% divided by 100 is 0.20 (or simply 0.2). We then multiply this decimal by the number we're finding the percentage of:
3000 x 0.2 = 600
Therefore, 20% of 3000 is 600.
Method 2: Using Fractions
As mentioned earlier, 20% is equivalent to the fraction 1/5. We can calculate 20% of 3000 by dividing 3000 by 5:
3000 / 5 = 600
This method provides a quicker calculation, especially when dealing with percentages that have simple fractional equivalents (like 20%, 25%, 50%, etc.).
Method 3: Using Proportions
This method utilizes the concept of proportions. We set up a proportion where we equate the ratio of the percentage to 100 with the ratio of the unknown value (x) to the total value (3000):
20/100 = x/3000
To solve for x, we cross-multiply:
20 * 3000 = 100 * x 60000 = 100x x = 60000 / 100 x = 600
This method demonstrates the underlying mathematical relationship between percentages and proportions, making it valuable for understanding the concept at a deeper level.
Real-World Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple arithmetic exercises. Here are some practical applications:
-
Finance: Calculating interest earned on savings accounts, determining discounts on sales, understanding tax rates, figuring out loan payments, and analyzing investment returns all rely heavily on percentage calculations. For example, if a bank offers a 5% annual interest rate on a savings account with a balance of $3000, you would earn $150 in interest ($3000 * 0.05 = $150).
-
Sales and Marketing: Businesses use percentages to determine profit margins, calculate discounts for promotions, and analyze sales performance. Understanding percentage change is vital for tracking sales growth or decline over time. For instance, if a company's sales increased from $2000 to $3000, the percentage increase is 50% (($3000 - $2000) / $2000 * 100 = 50%).
-
Science and Data Analysis: Percentages are fundamental in scientific research, statistical analysis, and data representation. Scientists often express their findings as percentages to convey proportions and probabilities. For example, a survey might reveal that 20% of participants prefer a certain product.
-
Everyday Life: Calculating tips in restaurants, understanding nutrition labels (percentage of daily value for nutrients), or determining the percentage of completion for a project all involve percentage calculations. Knowing how to quickly compute percentages allows for informed decision-making in daily life.
Beyond the Basics: Advanced Percentage Concepts
While calculating 20% of 3000 is a fundamental skill, understanding more advanced concepts can enhance your ability to work with percentages effectively:
-
Percentage Increase and Decrease: Calculating the percentage increase or decrease between two values requires understanding the formula: [(New Value - Old Value) / Old Value] * 100. This is useful for tracking changes in various metrics, such as stock prices, population growth, or economic indicators.
-
Percentage Points: It’s important to distinguish between percentage points and percentage change. A change from 20% to 30% is a 10 percentage point increase, but a 50% percentage increase (10/20 * 100 = 50%).
-
Compounding Percentages: Compounding refers to the process of earning interest on both the principal amount and accumulated interest. This is a crucial concept in finance, particularly in understanding the growth of investments over time.
-
Working with Multiple Percentages: Often, you'll need to calculate multiple percentages sequentially or simultaneously. For instance, applying a discount and then a sales tax.
Frequently Asked Questions (FAQs)
Q: How do I calculate a different percentage of 3000, say 15%?
A: You can use any of the methods described above, simply substituting 15% (or 0.15 as a decimal) for 20%. For example, using the decimal method: 3000 x 0.15 = 450.
Q: What if I need to find what percentage 600 is of 3000?
A: To find what percentage one number is of another, divide the first number by the second number and multiply by 100: (600 / 3000) * 100 = 20%.
Q: Are there any online calculators or tools that can help with percentage calculations?
A: Yes, many online calculators are readily available that can perform percentage calculations quickly and accurately. These can be particularly useful for more complex calculations.
Q: How can I improve my understanding of percentages?
A: Practice is key! Try solving various percentage problems using different methods. Understanding the underlying concepts of fractions, decimals, and proportions will strengthen your ability to tackle more advanced percentage calculations. Working through real-world examples will also solidify your comprehension.
Conclusion
Calculating 20% of 3000, while seemingly basic, serves as a gateway to understanding the broader application of percentages in various fields. Mastering percentage calculations empowers you to interpret data more effectively, make informed financial decisions, and navigate everyday situations with greater confidence. By understanding the various methods and their underlying principles, you can move beyond simple calculations and tackle more complex percentage problems with ease. The key is consistent practice and a deep understanding of the concepts involved. Remember that this fundamental skill is a valuable tool in both personal and professional settings, making it a worthwhile investment of your time and effort.
Latest Posts
Latest Posts
-
161 Minutes To Hours
Sep 14, 2025
-
Comedian George Carlin Quotes
Sep 14, 2025
-
Factor 2x 2 X
Sep 14, 2025
-
7 5 In A Fraction
Sep 14, 2025
-
Abiotic Factors Of Desert
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of 3000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.