219 Divided By 8
renascent
Sep 22, 2025 · 6 min read
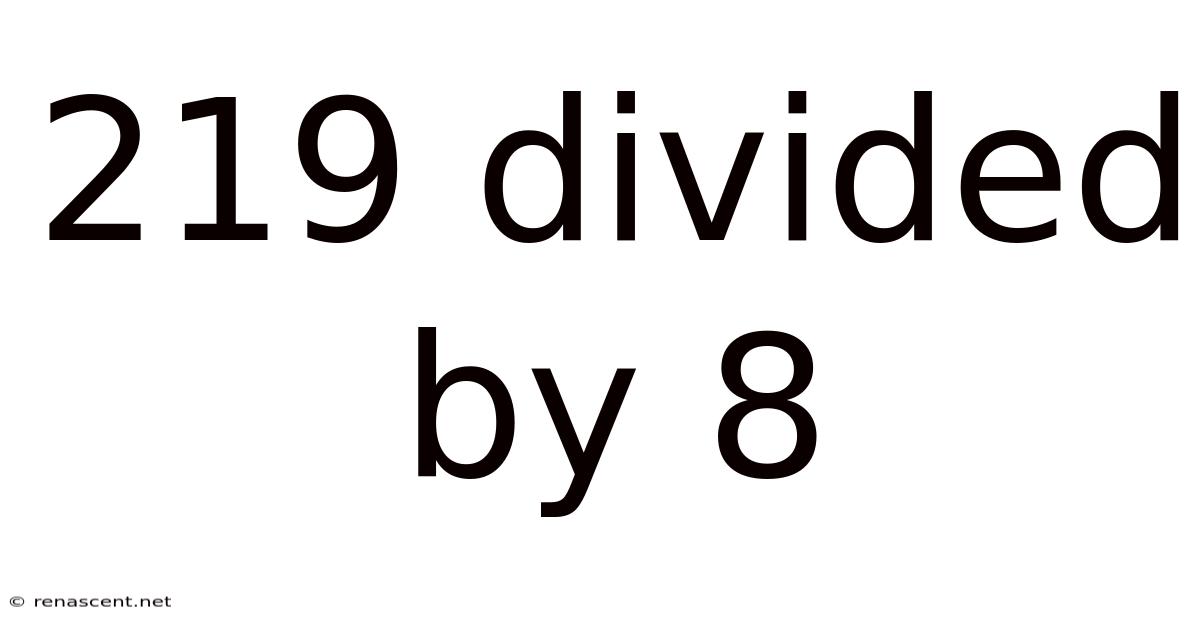
Table of Contents
Diving Deep into 219 Divided by 8: A Comprehensive Exploration of Division
This article explores the seemingly simple problem of 219 divided by 8, delving far beyond a mere numerical answer. We'll unravel the process, examine the different methods of solving it, and discuss the underlying mathematical concepts. Understanding division at this level is crucial for building a solid foundation in mathematics and developing problem-solving skills. This comprehensive guide will benefit students, educators, and anyone interested in gaining a deeper appreciation for arithmetic operations.
Introduction: More Than Just an Answer
The division problem 219 ÷ 8 might appear straightforward at first glance. Simply punching it into a calculator yields a decimal answer. However, a true understanding extends beyond obtaining a numerical result. This exploration will cover various approaches to solving the problem, emphasizing the conceptual understanding behind each method. We will cover long division, understanding remainders, and explore the practical applications of this type of calculation. We’ll also delve into related concepts such as fractions and decimals, showing how they interconnect and build upon each other.
Method 1: Long Division - A Step-by-Step Guide
Long division is a fundamental arithmetic process that systematically breaks down a division problem into smaller, manageable steps. Let's tackle 219 ÷ 8 using this method:
-
Setup: Write the problem in the long division format:
_____ 8 | 219 -
Divide the tens: How many times does 8 go into 21? The answer is 2 (8 x 2 = 16). Write the 2 above the 1 in 219.
2____ 8 | 219 -
Subtract: Subtract 16 from 21: 21 - 16 = 5.
2____ 8 | 219 -16 --- 5 -
Bring down the next digit: Bring down the 9 from 219, placing it next to the 5. You now have 59.
2____ 8 | 219 -16 --- 59 -
Divide the ones: How many times does 8 go into 59? The answer is 7 (8 x 7 = 56). Write the 7 above the 9 in 219.
27___ 8 | 219 -16 --- 59 -
Subtract: Subtract 56 from 59: 59 - 56 = 3.
27___ 8 | 219 -16 --- 59 -56 --- 3 -
Remainder: The 3 is the remainder. This means that 8 goes into 219 twenty-seven times with a remainder of 3.
Therefore, 219 ÷ 8 = 27 with a remainder of 3. We can express this as 27 R 3.
Method 2: Using Fractions
Division can also be represented as a fraction. The problem 219 ÷ 8 can be written as the fraction 219/8. This fraction represents the same value as the result of the long division.
To express this fraction as a mixed number (a whole number and a fraction), we perform the division:
219 ÷ 8 = 27 with a remainder of 3.
The whole number part of the mixed number is 27. The remainder (3) becomes the numerator of the fraction, and the divisor (8) remains the denominator. Therefore, 219/8 can be expressed as the mixed number 27 3/8.
Method 3: Decimal Representation
While long division gives us a whole number quotient and a remainder, we can also express the result as a decimal. Continuing the long division process beyond the remainder:
After obtaining the remainder 3, add a decimal point and a zero to the remainder (3.0). Now divide 30 by 8:
8 goes into 30 three times (8 x 3 = 24). This gives us 3 as the next digit in our decimal answer. The remainder is 6. Add another zero (60).
8 goes into 60 seven times (8 x 7 = 56). The remainder is 4. We can continue this process to obtain more decimal places but for practical purposes we might stop here.
Therefore, 219 ÷ 8 ≈ 27.375
Understanding Remainders
The remainder in a division problem represents the amount left over after the division is complete. In the case of 219 ÷ 8, the remainder is 3. This means that if we had 219 items to distribute equally among 8 groups, each group would receive 27 items, and there would be 3 items left over.
Remainders are essential in various real-world applications. For example, if you're dividing students into groups for a project, the remainder would represent the students who need to be added to an existing group or form a smaller group.
The Significance of the Decimal Representation
The decimal representation (27.375) offers a more precise representation of the result than the whole number with remainder (27 R 3). Decimals are crucial when dealing with measurements, percentages, and other situations requiring greater accuracy. The decimal form allows for more precise calculations and comparisons in various applications.
Practical Applications of Division
The ability to perform division accurately is fundamental to numerous practical applications across various fields:
- Resource allocation: Dividing resources (money, materials, time) equally among multiple recipients or projects.
- Measurement and scaling: Converting units, calculating averages, and determining proportions.
- Financial calculations: Calculating interest, dividing profits, and managing budgets.
- Engineering and design: Calculating dimensions, loads, and material requirements.
- Data analysis: Calculating averages, percentages, and ratios.
Frequently Asked Questions (FAQ)
-
Q: What is the most accurate way to represent the answer to 219 divided by 8?
A: The most accurate way is the decimal representation, 27.375, as it captures the entire value without losing information. However, depending on the context, the mixed number 27 3/8 or the whole number with a remainder 27 R 3 might be sufficient.
-
Q: Why do we use remainders?
A: Remainders provide essential information when we cannot achieve a perfect division. They show the amount left over, crucial for real-world problems involving distribution or measurement where fractional quantities might not be practical.
-
Q: Can I use a calculator for this problem?
A: Yes, a calculator provides a quick solution. However, understanding the underlying methods (long division, fractions) is vital for developing strong mathematical skills and solving more complex problems.
-
Q: What are the real-world applications of understanding division with remainders?
A: Understanding remainders is crucial in situations involving equal distribution where a perfect split isn’t possible. Think about distributing cookies evenly amongst friends or assigning tasks in a project.
Conclusion: A Deeper Understanding
Solving 219 ÷ 8 is more than simply getting the answer. This exploration aimed to move beyond a simple calculation and delve into the underlying principles of division, showcasing its versatility and importance in various mathematical contexts. Understanding different methods of calculation – long division, fractional representation, and decimal representation – is vital for building a solid mathematical foundation. The concepts of remainders and their practical applications further solidify this understanding, empowering you to tackle more complex problems and real-world scenarios with confidence. The ability to approach a seemingly simple problem like 219 ÷ 8 from multiple angles highlights the richness and depth of even fundamental mathematical concepts. By mastering these methods, you unlock a deeper understanding of the power and applicability of division in various aspects of life.
Latest Posts
Latest Posts
-
18 60 In Percentage
Sep 22, 2025
-
20 Of 1 3 Million
Sep 22, 2025
-
70 Miles Per Hour
Sep 22, 2025
-
1300 Divided By 5
Sep 22, 2025
-
Masque Meaning In Tempest
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 219 Divided By 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.