225 Divided By 3
renascent
Sep 23, 2025 · 6 min read
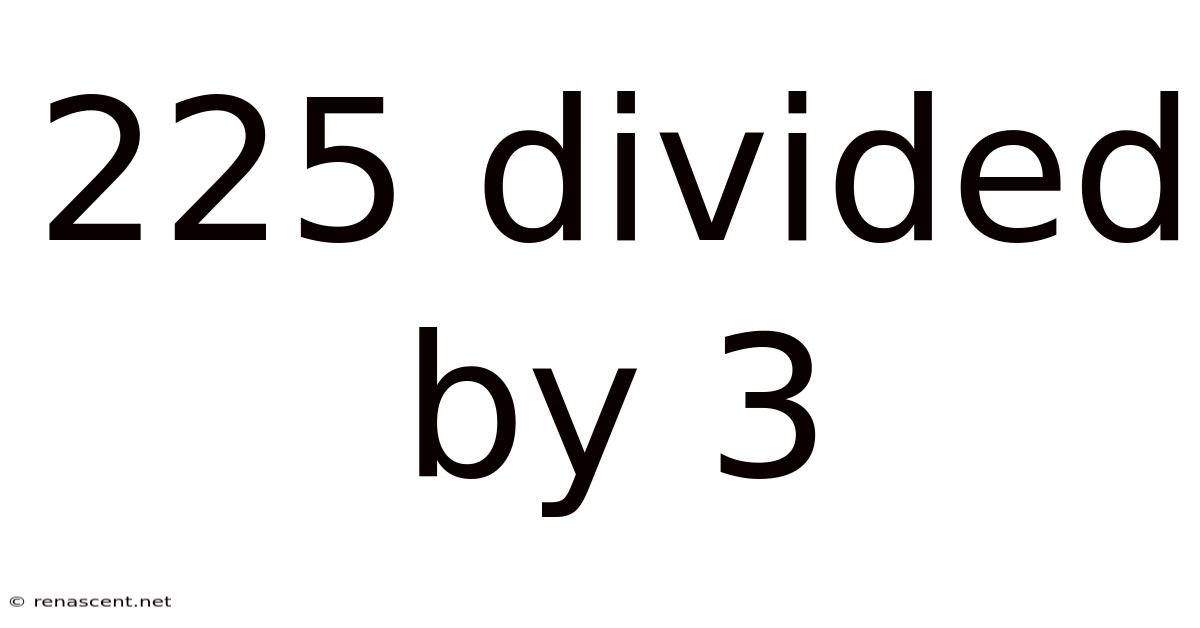
Table of Contents
225 Divided by 3: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 225 divided by 3, delving far beyond the immediate answer. We'll uncover the underlying principles of division, explore various methods for solving this problem, and examine its real-world applications across diverse fields. Understanding this basic operation unlocks a pathway to more complex mathematical concepts and problem-solving skills. This comprehensive guide is perfect for students, educators, and anyone curious about the beauty and practicality of mathematics.
Introduction: Understanding Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially represents the process of sharing or splitting a quantity into equal groups. In the expression 225 ÷ 3, we're asking: "If we have 225 items, and we want to divide them into 3 equal groups, how many items will be in each group?" The answer, as we'll soon discover, is 75. But the journey to finding this answer provides a rich opportunity to explore the mathematical concepts behind it.
Method 1: Long Division
Long division is a classic method for solving division problems, especially when dealing with larger numbers. It's a systematic approach that breaks the problem into smaller, manageable steps. Here's how to solve 225 ÷ 3 using long division:
-
Set up the problem: Write 225 inside the long division symbol (⟌) and 3 outside.
-
Divide the hundreds: How many times does 3 go into 2? It doesn't go in at all, so we move to the tens place.
-
Divide the tens: How many times does 3 go into 22? It goes in 7 times (7 x 3 = 21). Write 7 above the 2 in 225.
-
Subtract: Subtract 21 from 22, leaving a remainder of 1.
-
Bring down: Bring down the 5 from the ones place, creating the number 15.
-
Divide the ones: How many times does 3 go into 15? It goes in 5 times (5 x 3 = 15). Write 5 above the 5 in 225.
-
Subtract: Subtract 15 from 15, leaving a remainder of 0.
Therefore, 225 ÷ 3 = 75.
Method 2: Repeated Subtraction
This method is conceptually simpler, especially for beginners. It involves repeatedly subtracting the divisor (3) from the dividend (225) until you reach zero. Each subtraction represents one group.
- Start with 225.
- Subtract 3: 225 - 3 = 222
- Subtract 3 again: 222 - 3 = 219
- Continue subtracting 3 until you reach 0.
Counting the number of times you subtracted 3 will give you the answer. While tedious for larger numbers like 225, this method helps visually demonstrate the concept of division as repeated subtraction. For 225 divided by 3, you would perform this subtraction 75 times.
Method 3: Using Multiplication
Division and multiplication are inverse operations. This means that if you know the multiplication facts, you can use them to solve division problems. We're looking for a number that, when multiplied by 3, equals 225. Knowing your multiplication tables, or using a calculator, you'll quickly find that 75 x 3 = 225. Therefore, 225 ÷ 3 = 75.
The Scientific Explanation: Understanding Quotients and Remainders
From a purely mathematical perspective, division involves finding the quotient and the remainder. The quotient represents the number of times the divisor goes into the dividend evenly, while the remainder is what's left over. In the case of 225 ÷ 3, the quotient is 75, and the remainder is 0. This indicates that 3 divides 225 perfectly without any leftover.
Real-World Applications: Where Division Matters
The simple division of 225 by 3 might seem insignificant on its own, but the principle of division is fundamental to countless applications across various fields:
-
Everyday Life: Dividing up resources, sharing costs among friends, calculating portions, and determining unit prices all involve division. Imagine sharing 225 candies equally among 3 friends – each friend gets 75 candies.
-
Engineering and Design: Engineers frequently use division to calculate dimensions, material quantities, and load distribution. For example, dividing a 225-meter long bridge into 3 equal sections for construction purposes.
-
Computer Science: Division operations are at the core of many computer algorithms and programs, from data processing to game development.
-
Finance: Calculating interest rates, dividing investments, and determining profit margins heavily rely on division.
-
Science: Dividing experimental results, calculating averages, and converting units all require division. For instance, dividing the total weight of a sample by the number of units to find the average weight.
-
Cooking and Baking: Scaling recipes, dividing ingredients, and determining serving sizes involve the application of division principles.
Exploring Divisibility Rules: A Quick Check
Before engaging in long division, knowing divisibility rules can be helpful for quick estimations. A number is divisible by 3 if the sum of its digits is divisible by 3. In this case, 2 + 2 + 5 = 9, and 9 is divisible by 3, confirming that 225 is divisible by 3.
Beyond the Basics: Exploring Prime Factorization
Understanding prime factorization offers a deeper insight into the relationship between 225 and 3. The prime factorization of 225 is 3² x 5². This clearly shows that 225 contains the prime factor 3 (twice), explaining why it's divisible by 3.
Frequently Asked Questions (FAQ)
-
Q: What if the remainder wasn't 0? A: If the remainder was not 0, it would mean that 225 is not perfectly divisible by 3. For instance, if we were dividing 226 by 3, the quotient would be 75, and the remainder would be 1.
-
Q: Are there other ways to calculate 225 ÷ 3? A: Yes, you could use a calculator, a spreadsheet program, or even mental math techniques depending on your comfort level and the complexity of the problem.
-
Q: Why is division important? A: Division is a fundamental mathematical operation crucial for solving a vast array of problems in various fields, from everyday life to advanced scientific research. It's the basis for understanding ratios, proportions, and many other mathematical concepts.
-
Q: What happens if I divide by zero? A: Dividing by zero is undefined in mathematics. It's a concept that lacks a meaningful numerical interpretation.
Conclusion: The Significance of Simple Calculations
While 225 divided by 3 might seem like a trivial problem, it offers a gateway to exploring the wider world of mathematics and its pervasive applications. Mastering basic arithmetic operations like division is crucial for building a solid foundation in mathematics, empowering you to tackle more complex challenges with confidence and efficiency. Understanding the underlying principles, different methods of calculation, and real-world applications significantly enhances your mathematical literacy and problem-solving skills. The seemingly simple act of dividing 225 by 3 opens doors to a vast universe of mathematical exploration and understanding.
Latest Posts
Latest Posts
-
32 Cm To In
Sep 23, 2025
-
Ml To Micrograms Conversion
Sep 23, 2025
-
Mean Aerodynamic Chord Definition
Sep 23, 2025
-
4 6 As A Percentage
Sep 23, 2025
-
6 Multiples Of 9
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 225 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.