23 Divided By 3
renascent
Sep 19, 2025 · 6 min read
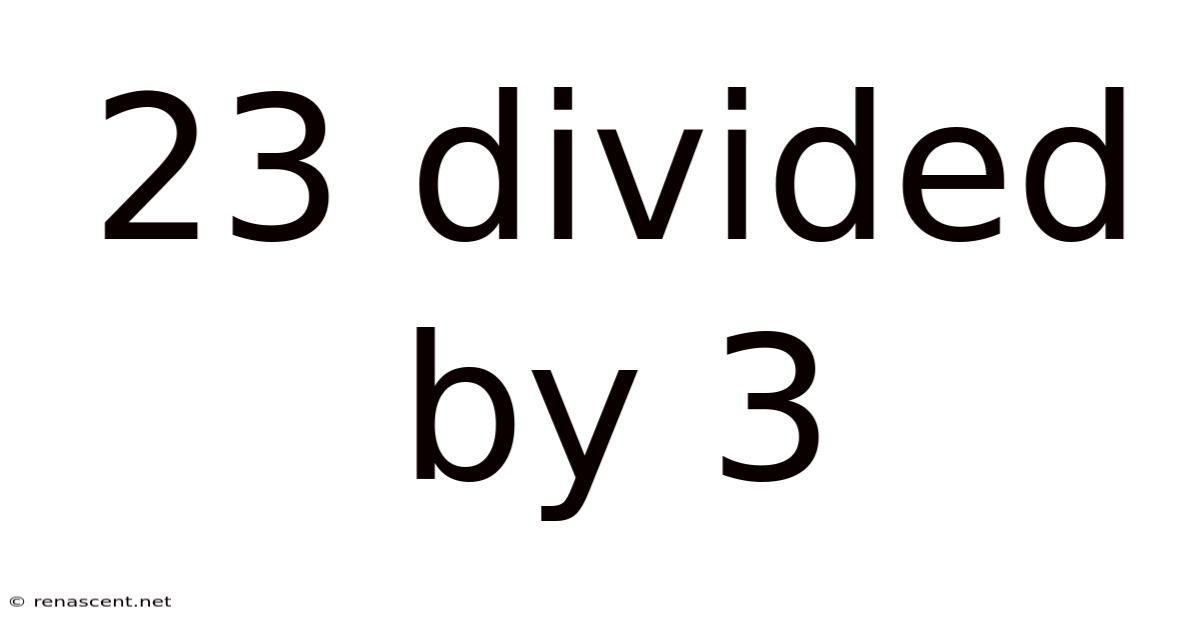
Table of Contents
23 Divided by 3: Exploring Division, Remainders, and Practical Applications
Dividing 23 by 3 might seem like a simple arithmetic problem, but it's a gateway to understanding fundamental mathematical concepts that extend far beyond basic calculations. This article delves deep into the intricacies of this seemingly straightforward division, exploring its result, the meaning of remainders, and how this type of problem finds practical applications in various fields. We’ll unpack the process, examine different methods of solving it, and delve into the underlying mathematical principles.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially asks the question: "How many times does one number fit into another?" In the case of 23 divided by 3 (written as 23 ÷ 3 or 23/3), we're asking how many times the number 3 goes into 23.
The basic components of a division problem are:
- Dividend: The number being divided (23 in this case).
- Divisor: The number we're dividing by (3 in this case).
- Quotient: The result of the division (the number of times the divisor goes into the dividend).
- Remainder: The amount left over after the division is complete.
Calculating 23 Divided by 3
Let's perform the division:
3 goes into 23 seven times (7 x 3 = 21). This is our quotient. However, there's still 2 left over (23 - 21 = 2). This is our remainder.
Therefore, 23 divided by 3 is 7 with a remainder of 2. This can be expressed in several ways:
- 7 R 2: This is a common shorthand notation, meaning 7 with a remainder of 2.
- 7 + 2/3: This shows the quotient (7) and the remainder (2) as a fraction of the divisor (3). This represents the complete answer as a mixed number.
- 7.666...: This is the decimal representation, where the "6" repeats infinitely. This is an example of a repeating decimal.
Different Methods of Division
While long division is a standard method, several other approaches can be used to solve 23 ÷ 3:
-
Long Division: This is the traditional method taught in schools, involving a step-by-step process of dividing, multiplying, subtracting, and bringing down digits.
-
Repeated Subtraction: This involves repeatedly subtracting the divisor (3) from the dividend (23) until the result is less than the divisor. The number of times you subtract is the quotient, and the remaining value is the remainder.
-
Multiplication and Estimation: You can estimate the quotient by thinking about multiples of 3. Since 3 x 7 = 21 and 3 x 8 = 24, you know the quotient is 7, and the difference between 23 and 21 (2) is the remainder.
The Significance of Remainders
The remainder in 23 ÷ 3 is not simply a leftover; it provides crucial information. It represents the portion of the dividend that cannot be evenly divided by the divisor. This has implications in various contexts:
-
Real-world Scenarios: Imagine you have 23 apples and want to distribute them equally among 3 friends. Each friend gets 7 apples (the quotient), and you have 2 apples left over (the remainder).
-
Fractions and Decimals: The remainder can be expressed as a fraction (2/3) or a decimal (0.666...). This provides a more precise representation of the division than just the whole number quotient.
-
Modular Arithmetic: In modular arithmetic, the remainder is the key element. For example, in a 12-hour clock, adding 23 hours is equivalent to adding 11 hours (23 ÷ 12 = 1 R 11). The remainder (11) determines the final time.
Applications of Division with Remainders
The concept of division with a remainder finds wide-ranging applications across various fields:
-
Computer Science: Remainders are fundamental in computer algorithms and data structures. For example, the modulo operator (%) provides the remainder of a division, used in tasks like hashing, encryption, and random number generation.
-
Engineering and Design: Division with remainders is crucial in tasks involving resource allocation, material cutting, and spatial planning. For example, determining how many complete units can be produced from a given quantity of raw material, considering potential waste.
-
Finance: Dividing profits amongst shareholders, calculating interest rates, or distributing funds equally among different accounts involve division with remainders.
-
Scheduling and Time Management: Determining the number of complete work shifts given a total number of hours available, or planning project timelines involves calculating quotients and remainders.
-
Physics and Chemistry: Calculating proportions of substances, distribution of forces, and determining reaction rates often require calculations that incorporate remainders.
Beyond Simple Division: Exploring Deeper Concepts
The seemingly simple problem of 23 ÷ 3 opens doors to more complex mathematical ideas:
-
Prime Numbers and Divisibility: Understanding the factors of a number—numbers that divide evenly without a remainder—is essential in number theory. 23 is a prime number because its only factors are 1 and 23.
-
Greatest Common Divisor (GCD): Finding the largest number that divides two or more numbers evenly is crucial in various mathematical applications, including simplifying fractions.
-
Least Common Multiple (LCM): Finding the smallest number that is a multiple of two or more numbers is used in solving problems involving cycles and patterns.
Frequently Asked Questions (FAQ)
Q: What is the most accurate way to represent 23 divided by 3?
A: The most accurate representation depends on the context. For practical purposes, 7 R 2 or 7 2/3 is sufficient. For precise mathematical calculations, the decimal representation (7.666...) might be preferred, understanding it's a repeating decimal.
Q: Can the remainder ever be larger than the divisor?
A: No. If the remainder is larger than the divisor, it means the division wasn't done correctly. The remainder must always be smaller than the divisor.
Q: Why is understanding remainders important?
A: Remainders provide crucial information about the incomplete nature of a division. They represent the "leftover" portion and are essential in numerous real-world applications and advanced mathematical concepts.
Q: How do I solve more complex division problems with larger numbers?
A: For larger numbers, long division or a calculator is generally the most efficient approach. However, the underlying principles remain the same: understanding the quotient, the remainder, and their significance.
Conclusion
The simple act of dividing 23 by 3 reveals a wealth of mathematical concepts and practical applications. From understanding basic arithmetic operations to delving into complex algorithms and real-world scenarios, the seemingly insignificant act of division provides a profound insight into the power and relevance of mathematics in our daily lives. Mastering this fundamental concept lays a strong foundation for tackling more advanced mathematical challenges. Remember, the journey of understanding mathematics begins with these seemingly simple yet fundamental building blocks, and each concept builds upon the others, creating a powerful and versatile knowledge base.
Latest Posts
Latest Posts
-
220 Lbs In Kilos
Sep 19, 2025
-
95 Minutes To Hours
Sep 19, 2025
-
Phosphorus Lewis Dot Structure
Sep 19, 2025
-
66 F To Celsius
Sep 19, 2025
-
Kashyap Is Which Caste
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 23 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.