23 Divided By 5
renascent
Sep 15, 2025 · 5 min read
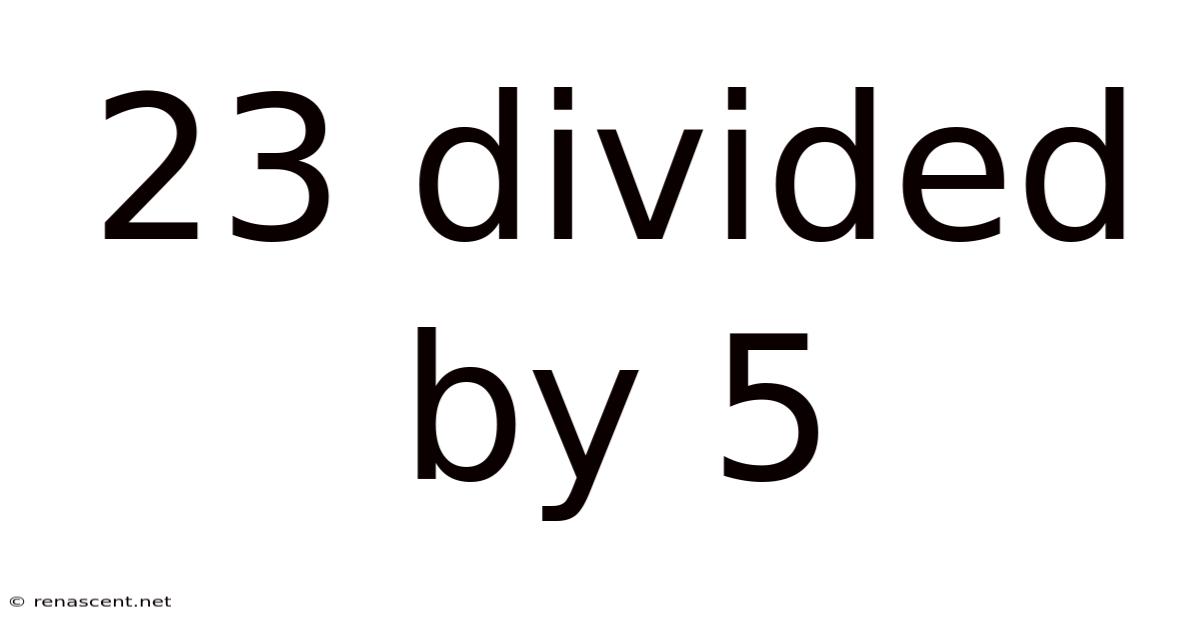
Table of Contents
Diving Deep into 23 Divided by 5: A Comprehensive Exploration of Division
This article provides a comprehensive exploration of the seemingly simple mathematical problem: 23 divided by 5. While the initial calculation might seem straightforward, a deeper dive reveals several important mathematical concepts applicable across various levels of mathematical understanding. We'll explore the process, different methods of solving it, its application in real-world scenarios, and address common misconceptions. Understanding this seemingly basic problem lays a strong foundation for more complex mathematical operations.
Understanding Division: A Foundational Concept
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of 23 divided by 5 (often written as 23 ÷ 5 or 23/5), we are asking: "How many times does 5 fit into 23?"
Methods for Solving 23 Divided by 5
There are several ways to approach this division problem, each offering valuable insights into the nature of division:
1. Long Division:
This is a traditional method taught in elementary schools. It involves a systematic process of dividing, multiplying, subtracting, and bringing down digits.
4
5 | 23
-20
3
This shows that 5 goes into 23 four times (4 x 5 = 20), with a remainder of 3. Therefore, 23 divided by 5 is 4 with a remainder of 3.
2. Repeated Subtraction:
This method visually demonstrates the concept of repeatedly subtracting the divisor (5) from the dividend (23) until the remainder is less than the divisor.
- 23 - 5 = 18
- 18 - 5 = 13
- 13 - 5 = 8
- 8 - 5 = 3
We subtracted 5 four times before reaching a remainder of 3. Again, the result is 4 with a remainder of 3.
3. Fraction Representation:
Division can also be represented as a fraction. 23 divided by 5 can be written as 23/5. This fraction represents the division problem and can be used to further understand the result.
4. Decimal Representation:
Instead of expressing the result with a remainder, we can convert it to a decimal. To do this, we continue the long division process:
4.6
5 | 23.0
-20
30
-30
0
This shows that 23 divided by 5 is 4.6. The decimal representation provides a more precise answer than the whole number with a remainder.
Interpreting the Results: Remainders and Decimals
The choice between representing the answer as a whole number with a remainder (4 R3) or a decimal (4.6) depends on the context of the problem.
-
Remainders: Remainders are useful when dealing with discrete quantities that cannot be easily divided. For example, if you have 23 apples and want to divide them equally among 5 people, each person gets 4 apples, and 3 apples are left over.
-
Decimals: Decimals are more useful when dealing with continuous quantities, such as measuring length or weight. If you have 23 meters of rope and want to cut it into 5 equal pieces, each piece would be 4.6 meters long.
Real-World Applications: Where Division Matters
Understanding division, even in the context of 23 divided by 5, is crucial for navigating various real-world scenarios:
- Sharing Resources: Dividing resources equally (money, food, tasks) amongst a group of people.
- Calculating Averages: Finding the average score on a test, average speed, or average temperature.
- Scaling Recipes: Adjusting the ingredients in a recipe to serve more or fewer people.
- Unit Conversions: Converting units of measurement (e.g., converting kilometers to miles).
- Financial Calculations: Calculating interest rates, unit costs, or profit margins.
- Geometric Problems: Calculating areas, volumes, or proportions of shapes.
Beyond the Basics: Exploring More Advanced Concepts
The simple problem of 23 divided by 5 opens doors to more complex mathematical concepts:
- Prime Factorization: Understanding the prime factors of 23 (23 is a prime number) and 5 helps in more complex division problems involving larger numbers.
- Modular Arithmetic: The remainder (3) in the problem 23 ÷ 5 is the basis for modular arithmetic, a branch of number theory with applications in cryptography and computer science.
- Fractions and Decimals: Converting between fractions and decimals is a fundamental skill that builds upon the understanding of division.
- Ratio and Proportion: Division is an integral part of understanding ratios and proportions, which are used extensively in scaling, mixing, and comparing quantities.
Addressing Common Misconceptions
- Ignoring Remainders: It's crucial to understand the significance of remainders, as they provide crucial information in many real-world contexts. Simply truncating the remainder can lead to inaccurate results.
- Confusing Division with Other Operations: Students often confuse division with other operations like subtraction or multiplication. A clear understanding of the concept is essential to avoid errors.
- Difficulty with Decimal Representation: Converting remainders to decimals requires a strong understanding of place value and decimal notation.
Frequently Asked Questions (FAQ)
Q: What is the remainder when 23 is divided by 5?
A: The remainder is 3.
Q: Is 23/5 a proper or improper fraction?
A: 23/5 is an improper fraction because the numerator (23) is greater than the denominator (5).
Q: How do I convert 23/5 to a mixed number?
A: To convert 23/5 to a mixed number, divide 23 by 5. The quotient (4) becomes the whole number part, and the remainder (3) becomes the numerator of the fraction, with the denominator remaining as 5. So, 23/5 = 4 3/5.
Q: What are some real-world examples where understanding 23 divided by 5 is important?
A: Examples include sharing 23 candies among 5 friends, calculating the average score from 5 tests with a total score of 23, or determining the length of each piece if you divide a 23-meter rope into 5 equal pieces.
Q: Why is it important to learn different methods of division?
A: Learning multiple methods helps build a deeper understanding of the concept, strengthens problem-solving skills, and allows for flexibility in choosing the most appropriate method depending on the problem's complexity and context.
Conclusion: A Deeper Appreciation of Division
While seemingly simple, the problem of 23 divided by 5 serves as a gateway to understanding fundamental mathematical concepts. From the basics of long division to the complexities of modular arithmetic and decimal representation, this seemingly simple calculation opens a world of mathematical possibilities. Mastering this basic operation builds a strong foundation for more advanced mathematical skills and fosters a deeper appreciation for the practical applications of mathematics in our daily lives. By exploring different methods and understanding the nuances of remainders and decimals, we develop a comprehensive understanding of division and its far-reaching implications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 23 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.