24 Devided By 4
renascent
Sep 19, 2025 · 6 min read
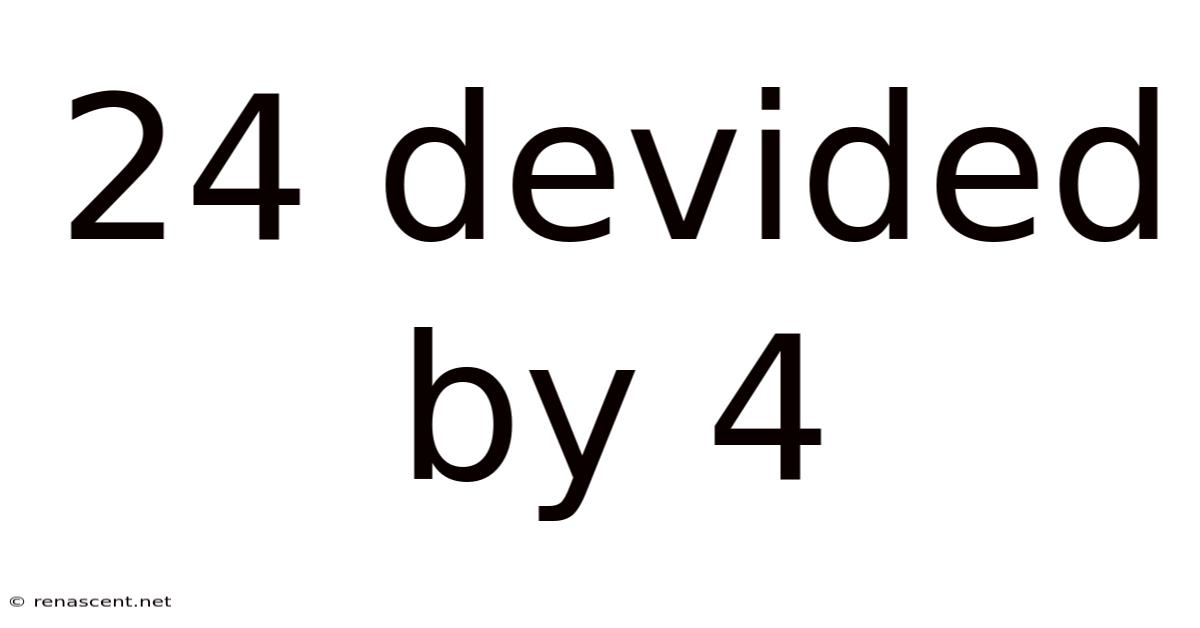
Table of Contents
24 Divided by 4: A Deep Dive into Division and its Applications
Introduction:
The seemingly simple calculation of 24 divided by 4 (24 ÷ 4) serves as a gateway to understanding fundamental mathematical concepts. This article explores this basic division problem, delving beyond the answer to examine the underlying principles of division, its various applications in everyday life, and its significance in more advanced mathematical fields. We'll explore different methods of solving this problem, discuss its real-world implications, and address some frequently asked questions. This comprehensive guide aims to provide a thorough understanding of division, not just for beginners but also for those looking to solidify their foundational math skills. We'll cover everything from basic arithmetic to the conceptual underpinnings of division, ensuring a complete and enriching learning experience.
Understanding Division: The Concept
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the inverse operation of multiplication. While multiplication involves combining equal groups, division involves separating a quantity into equal groups or determining how many times one number is contained within another. In the context of 24 ÷ 4, we're asking: "How many times does 4 fit into 24?" or "If we divide 24 into 4 equal groups, how many are in each group?"
The components of a division problem are:
- Dividend: The number being divided (24 in this case).
- Divisor: The number we are dividing by (4 in this case).
- Quotient: The result of the division (the answer).
- Remainder: The amount left over if the division isn't perfectly even (0 in this case).
Methods for Solving 24 ÷ 4
Several methods can be employed to solve 24 ÷ 4, catering to different learning styles and levels of understanding:
1. Repeated Subtraction: This method involves repeatedly subtracting the divisor (4) from the dividend (24) until you reach zero. The number of times you subtract is the quotient.
- 24 - 4 = 20
- 20 - 4 = 16
- 16 - 4 = 12
- 12 - 4 = 8
- 8 - 4 = 4
- 4 - 4 = 0
We subtracted 4 six times, so 24 ÷ 4 = 6.
2. Multiplication Facts: If you know your multiplication tables, you can easily find the answer. Since 4 x 6 = 24, then 24 ÷ 4 = 6. This method relies on the inverse relationship between multiplication and division.
3. Long Division: This is a more formal method, particularly useful for larger numbers. While less necessary for 24 ÷ 4, it's essential to understand for more complex division problems.
6
4 | 24
-24
0
We ask: "How many times does 4 go into 2?" (zero times). Then we consider "How many times does 4 go into 24?" (six times). 4 x 6 = 24, and subtracting leaves a remainder of 0.
4. Visual Representation: You can visualize this problem using objects. Imagine 24 objects arranged into 4 equal groups. Counting the number of objects in each group will yield the answer, 6.
Real-World Applications of Division
Division isn't confined to the classroom; it’s a crucial skill applied in various real-world scenarios:
-
Sharing Equally: Dividing a pizza among friends, distributing candies amongst children, or splitting a bill among diners all involve division.
-
Measurement and Conversion: Converting larger units to smaller ones (e.g., converting 24 inches into feet, knowing there are 12 inches in a foot: 24 ÷ 12 = 2 feet) uses division.
-
Calculating Unit Rates: Determining the price per unit (e.g., cost per ounce, kilometers per liter) relies on division. If a 24-ounce bottle of juice costs $4, the price per ounce is $4 ÷ 24 ounces.
-
Averaging: Finding the average of a set of numbers involves summing the numbers and then dividing by the count of numbers. For example, the average of 20, 24, and 28 is (20 + 24 + 28) ÷ 3 = 24.
-
Scaling Recipes: Adjusting recipes to serve more or fewer people requires dividing or multiplying ingredient quantities.
-
Data Analysis: Division plays a crucial role in many data analysis tasks, from calculating percentages to determining averages and rates of change.
Division in Advanced Mathematics
The seemingly basic operation of division forms the foundation for many more advanced mathematical concepts:
-
Fractions: Division is intrinsically linked to fractions. The fraction 24/4 is equivalent to 24 ÷ 4.
-
Algebra: Solving algebraic equations often involves division to isolate variables.
-
Calculus: Differential and integral calculus use division extensively in various operations like derivatives and integrals.
-
Statistics: Division is integral to statistical calculations, such as calculating means, variances, and standard deviations.
Beyond the Basics: Exploring Divisibility Rules
While solving 24 ÷ 4 is straightforward, understanding divisibility rules can enhance your mathematical intuition. Divisibility rules provide quick ways to determine if a number is divisible by another without performing the actual division. For 4, the rule is: A number is divisible by 4 if its last two digits are divisible by 4. Since the last two digits of 24 (24) are divisible by 4 (24 ÷ 4 = 6), we know 24 is divisible by 4.
Understanding these rules can speed up calculations and aid in problem-solving.
Frequently Asked Questions (FAQ)
Q: What if the division doesn't result in a whole number?
A: If the division doesn't result in a whole number, you'll have a remainder. For example, 25 ÷ 4 = 6 with a remainder of 1. This can be expressed as a fraction (6 1/4) or a decimal (6.25).
Q: How can I improve my division skills?
A: Practice is key! Start with simple problems and gradually increase the difficulty. Use different methods to solve the problems, and try to understand the underlying concepts rather than just memorizing steps. Regular practice and using various resources like worksheets, online games, and educational apps can help significantly.
Q: What are some common mistakes people make when dividing?
A: Common mistakes include errors in carrying over digits in long division, forgetting to account for remainders, and misinterpreting the order of operations when division is combined with other arithmetic operations. Careful attention to detail and understanding the steps involved can help avoid these mistakes.
Conclusion
The simple calculation of 24 divided by 4, while seemingly elementary, provides a valuable opportunity to explore the fundamental principles of division and its wide-ranging applications. From everyday tasks to advanced mathematical concepts, division proves to be an indispensable tool. Mastering this foundational operation is not merely about finding the answer (which is 6); it’s about understanding the process, appreciating its versatility, and building a strong foundation for more complex mathematical endeavors. The journey from understanding a simple division problem to grasping its implications across various mathematical fields underscores the importance of continuous learning and the interconnectedness of mathematical concepts. By understanding the "why" behind the "how," you build a stronger mathematical understanding, ready for the challenges and opportunities that lie ahead.
Latest Posts
Latest Posts
-
Phosphorus Lewis Dot Structure
Sep 19, 2025
-
66 F To Celsius
Sep 19, 2025
-
Kashyap Is Which Caste
Sep 19, 2025
-
Factorise X Squared 16
Sep 19, 2025
-
Are Black Panthers Endangered
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 24 Devided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.