24 Divided By 3
renascent
Sep 22, 2025 · 6 min read
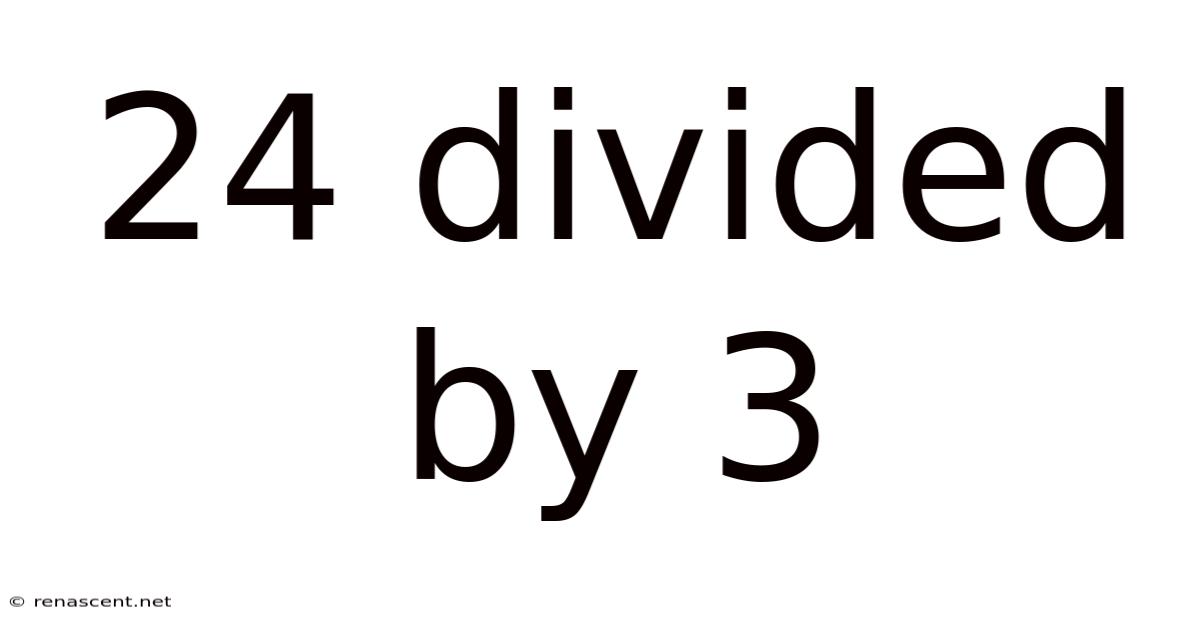
Table of Contents
24 Divided by 3: A Deep Dive into Division and its Applications
This article explores the seemingly simple equation of 24 divided by 3, delving far beyond the basic answer. We'll examine the fundamental principles of division, explore various methods for solving this problem, and uncover its practical applications in diverse fields. Understanding this seemingly simple calculation unlocks a deeper comprehension of mathematical concepts crucial for everyday life and advanced studies. We'll even touch upon the historical context of division and its evolution throughout human history.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a whole quantity into equal parts. In the equation 24 ÷ 3, we're essentially asking: "If we have 24 items, and we want to divide them equally into 3 groups, how many items will be in each group?" The answer, as we'll soon demonstrate through multiple methods, is 8. But understanding why this is the answer is far more important than simply knowing the result.
Methods for Solving 24 ÷ 3
There are several ways to solve 24 divided by 3, catering to different learning styles and levels of mathematical understanding. Let's explore a few:
1. Repeated Subtraction: This is a foundational method, particularly useful for visualizing the division process. We repeatedly subtract the divisor (3) from the dividend (24) until we reach zero. The number of times we subtract represents the quotient.
- 24 - 3 = 21
- 21 - 3 = 18
- 18 - 3 = 15
- 15 - 3 = 12
- 12 - 3 = 9
- 9 - 3 = 6
- 6 - 3 = 3
- 3 - 3 = 0
We subtracted 3 eight times, therefore, 24 ÷ 3 = 8.
2. Multiplication's Inverse: Division is the inverse operation of multiplication. To solve 24 ÷ 3, we can ask: "What number, when multiplied by 3, equals 24?" This is a simpler way to frame the problem for many. The answer, again, is 8 (because 3 x 8 = 24).
3. Long Division: This is a more formal method, typically taught in elementary school and essential for handling larger division problems.
8
3 | 24
-24
0
We ask how many times 3 goes into 2 (it doesn't, so we move to 24). 3 goes into 24 eight times (3 x 8 = 24). We subtract 24 from 24, leaving a remainder of 0. Therefore, 24 ÷ 3 = 8.
4. Using a Number Line: A visual approach, particularly helpful for younger learners. Start at 24 on a number line and repeatedly jump back 3 units until you reach 0. The number of jumps equals the quotient.
The Significance of Remainders
While 24 divided by 3 results in a whole number (8) with no remainder, it's crucial to understand how remainders work in division. If we were to divide 25 by 3, we'd get 8 with a remainder of 1. This means that we can divide 25 into groups of 3 eight times, with one item left over. Remainders are essential in various applications, such as determining the number of whole groups we can form and what's left over.
Real-World Applications of Division: Beyond the Classroom
The seemingly simple act of dividing 24 by 3 has far-reaching applications in numerous real-world scenarios:
- Sharing Equally: Dividing 24 cookies among 3 friends requires this basic calculation to ensure everyone gets an equal share of 8 cookies.
- Calculating Unit Price: If 3 apples cost $24, the unit price per apple is calculated by dividing $24 by 3, resulting in $8 per apple.
- Resource Allocation: In business or project management, dividing resources (budget, time, personnel) among different tasks or teams frequently involves this fundamental operation.
- Geometry and Measurement: Division is essential in various geometric calculations, such as finding the side length of a square given its area.
- Data Analysis and Statistics: Calculating averages, mean values, and proportions frequently involves division. For example, determining the average score on a test with 24 total points scored by 3 students.
- Computer Science: Division is a fundamental operation in programming and algorithm design, crucial for tasks ranging from image processing to data sorting.
- Engineering and Physics: Division is involved in numerous calculations in various engineering and physics disciplines including calculating speeds, forces, and various aspects of mechanical design.
Historical Context of Division
The concept of division, though seemingly simple, has a rich history. Ancient civilizations developed various methods for dividing numbers, often employing tools like counting boards or abaci. The Babylonians, Egyptians, and Greeks each developed their approaches to division, laying the foundation for the methods we use today. The development of the Hindu-Arabic numeral system and the concept of zero significantly simplified the process of division, allowing for more efficient and widespread calculation.
Division and Fractions
Understanding division is intrinsically linked to understanding fractions. The expression 24 ÷ 3 can be represented as the fraction 24/3. This fraction simplifies to 8/1, which is equivalent to 8. This connection highlights the close relationship between division and representing parts of a whole.
Beyond Basic Division: Exploring Advanced Concepts
While 24 ÷ 3 is a basic calculation, it serves as a springboard to more complex mathematical concepts:
- Divisibility Rules: Understanding divisibility rules helps us quickly determine whether a number is divisible by another without performing the full division. For instance, a number is divisible by 3 if the sum of its digits is divisible by 3. Since 2 + 4 = 6, and 6 is divisible by 3, we know that 24 is divisible by 3.
- Prime Factorization: Breaking down a number into its prime factors (numbers divisible only by 1 and themselves) is a crucial concept in number theory. 24 can be factorized as 2 x 2 x 2 x 3 (or 2³ x 3).
- Modular Arithmetic: This branch of number theory deals with remainders in division. For example, in modular arithmetic (mod 3), 24 is congruent to 0, because 24 divided by 3 leaves a remainder of 0.
- Algebra: Division plays a central role in solving algebraic equations and manipulating algebraic expressions.
- Calculus: Division is fundamental in the concepts of derivatives and integrals in calculus.
Frequently Asked Questions (FAQ)
- Q: What happens if I divide by zero? A: Dividing by zero is undefined in mathematics. It's a fundamental concept that has no solution.
- Q: What if I'm dividing larger numbers? A: For larger numbers, using long division or a calculator becomes more practical.
- Q: Are there different types of division? A: Yes, there are different types of division, including integer division (where only the whole number result is given), and floating-point division (where decimal results are permitted).
- Q: How can I improve my division skills? A: Practice is key! Start with simple problems, gradually increasing the complexity. Use different methods to reinforce your understanding.
Conclusion: The Enduring Importance of Division
The seemingly simple equation 24 ÷ 3 = 8 underscores the fundamental importance of division in mathematics and its wide-ranging applications in daily life and various fields. By understanding the underlying principles, exploring different solution methods, and grasping its practical applications, we can appreciate the power and versatility of this essential arithmetic operation. It's not just about getting the right answer; it's about understanding the process, its implications, and its significance in shaping our understanding of the world around us. Mastering division isn't just about solving math problems; it's about unlocking a deeper understanding of numbers and their relationship to our reality.
Latest Posts
Latest Posts
-
Positive Feedback Giving Birth
Sep 22, 2025
-
0 005 As A Fraction
Sep 22, 2025
-
Carpet Cleaning Solution Homemade
Sep 22, 2025
-
1 94 M To Ft
Sep 22, 2025
-
Verily A New Hope
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 24 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.