24 Divided By 5
renascent
Sep 17, 2025 · 6 min read
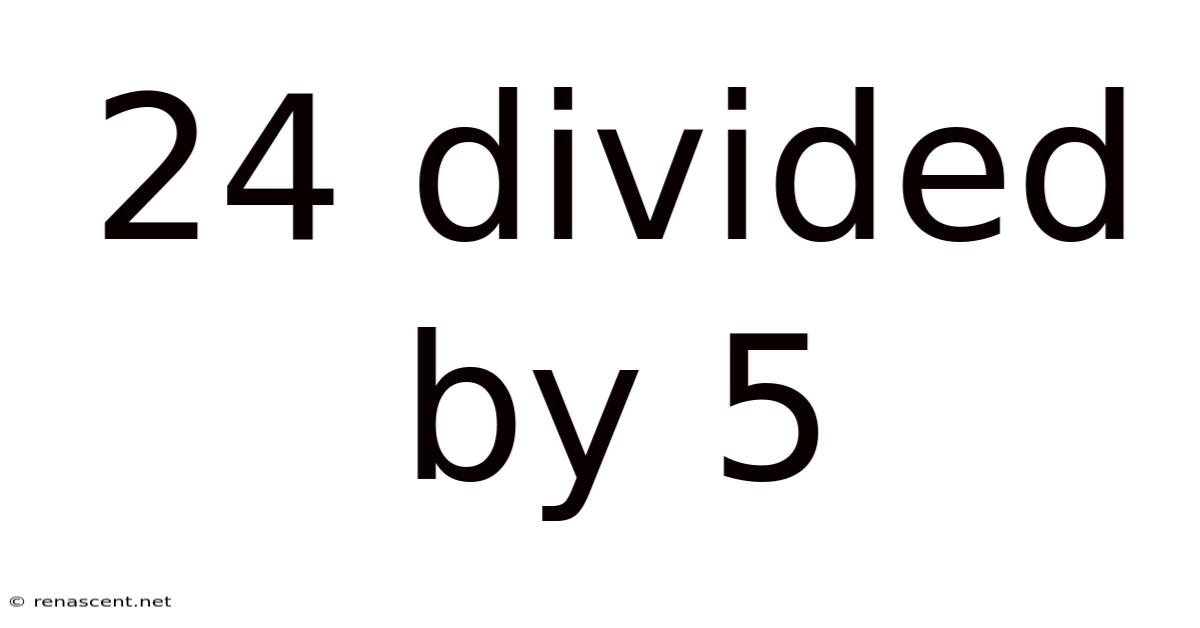
Table of Contents
Unveiling the Mystery: A Deep Dive into 24 Divided by 5
This article explores the seemingly simple calculation of 24 divided by 5, delving far beyond the basic answer. We'll unravel the different approaches to solving this problem, discuss the underlying mathematical concepts, and explore the practical applications of division in everyday life. Understanding this seemingly simple equation opens doors to a deeper understanding of mathematics and its real-world relevance. We’ll cover everything from basic division to the nuances of remainders and their interpretations. This comprehensive guide will leave you with a complete understanding of 24 divided by 5 and related concepts.
The Basic Calculation: Quotient and Remainder
The most straightforward way to solve 24 divided by 5 is through long division. This method provides both the quotient (the result of the division) and the remainder (the amount left over).
Let's walk through the process:
-
Set up the long division: Write 24 as the dividend (the number being divided) inside the division symbol, and 5 as the divisor (the number you're dividing by) outside.
-
Divide: How many times does 5 go into 2? It doesn't go in at all, so we move to the next digit. How many times does 5 go into 24? It goes in 4 times (5 x 4 = 20). Write the 4 above the 4 in 24.
-
Multiply: Multiply the quotient (4) by the divisor (5): 4 x 5 = 20. Write this underneath the 24.
-
Subtract: Subtract 20 from 24: 24 - 20 = 4. This is the remainder.
Therefore, 24 divided by 5 is 4 with a remainder of 4. We can express this as: 24 ÷ 5 = 4 R 4
Representing the Answer: Fractions and Decimals
While the remainder is crucial, it doesn't tell the whole story. We can express the result more completely using fractions or decimals.
Fraction Representation
The remainder (4) can be written as a fraction with the divisor (5) as the denominator: 4/5. This represents the portion of the divisor that remains. So, 24 divided by 5 can also be expressed as 4 4/5. This mixed number clearly shows both the whole number quotient (4) and the fractional remainder (4/5).
Decimal Representation
To obtain a decimal representation, we can further divide the remainder by the divisor. We can add a decimal point and a zero to the remainder, making it 4.0. Then, we continue the division:
5 goes into 40 eight times (5 x 8 = 40). This means that the decimal equivalent of 4/5 is 0.8.
Therefore, 24 divided by 5 can also be expressed as 4.8.
Understanding the Concepts: Division, Quotient, Remainder, and Divisibility
Let's delve into the fundamental mathematical concepts behind this calculation.
-
Division: Division is one of the four basic arithmetic operations, the inverse of multiplication. It involves splitting a quantity into equal parts.
-
Quotient: The quotient is the result of the division process; it represents how many times the divisor goes into the dividend.
-
Remainder: The remainder is the amount left over after the division process. If the remainder is zero, we say that the dividend is divisible by the divisor.
-
Divisibility: A number is divisible by another number if the division results in a whole number (i.e., a remainder of zero). 24 is not divisible by 5 because the remainder is 4.
Practical Applications of Division and Remainders
Division, along with its quotient and remainder, plays a vital role in numerous real-world scenarios:
-
Sharing: Imagine you have 24 cookies to share equally among 5 friends. Each friend would receive 4 cookies (the quotient), and you would have 4 cookies left over (the remainder).
-
Measurement: If you have a 24-meter rope and need to cut it into 5-meter pieces, you could create 4 pieces (the quotient) with 4 meters remaining (the remainder).
-
Pricing: If an item costs $24 and you want to split the cost among 5 people, each person would pay $4.80.
-
Programming: Remainders are often used in computer programming for tasks like determining if a number is even or odd (divisible by 2) or for creating patterns and loops.
-
Engineering: Many engineering calculations involve division and remainders, for example, in determining the number of components needed for a project.
Beyond the Basics: Exploring Different Methods
While long division is the most common approach, other methods can be used to solve 24 divided by 5.
Repeated Subtraction
Repeatedly subtract the divisor (5) from the dividend (24) until you reach a number less than the divisor. The number of times you subtract is the quotient, and the remaining number is the remainder.
24 - 5 = 19 19 - 5 = 14 14 - 5 = 9 9 - 5 = 4
We subtracted 5 four times, giving us a quotient of 4 and a remainder of 4.
Frequently Asked Questions (FAQ)
Q: What is the most accurate way to represent 24 divided by 5?
A: The most accurate representation depends on the context. For practical applications like sharing items, 4 R 4 or 4 4/5 might be sufficient. For financial calculations, 4.8 is preferred.
Q: Can the remainder ever be larger than the divisor?
A: No. If the remainder is larger than the divisor, it means you haven't divided completely. You can still continue the division process until the remainder is smaller than the divisor.
Q: What if I need to divide a much larger number?
A: The same principles apply. You can use long division or a calculator for larger numbers.
Q: Are there any real-world examples where the decimal representation is more useful than the fraction or remainder?
A: Yes, decimal representation is crucial in many situations, especially those involving money, measurements (like using a ruler or measuring tape), and scientific calculations where precision is critical.
Conclusion: Mastering the Fundamentals of Division
This in-depth exploration of 24 divided by 5 reveals that even a seemingly simple calculation can provide a rich understanding of fundamental mathematical principles. By mastering the concepts of division, quotients, remainders, and different representation methods (fractions and decimals), you'll develop a strong foundation for more complex mathematical concepts and real-world problem-solving. Remember the core message: understanding the 'why' behind the calculation is just as important as finding the answer itself. This holistic approach empowers you to not just calculate but to truly understand the mathematics at play. The ability to confidently interpret and apply these principles will significantly improve your problem-solving capabilities in various aspects of your life, both academic and professional. The simple equation of 24 divided by 5 serves as a gateway to a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Flare Fitting Copper Tubing
Sep 17, 2025
-
Formula Of Aluminium Nitrate
Sep 17, 2025
-
1030 Mm To Inches
Sep 17, 2025
-
96 F In Celsius
Sep 17, 2025
-
Ac Induction Motor Diagram
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 24 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.