25 Divided By 2
renascent
Sep 21, 2025 · 6 min read
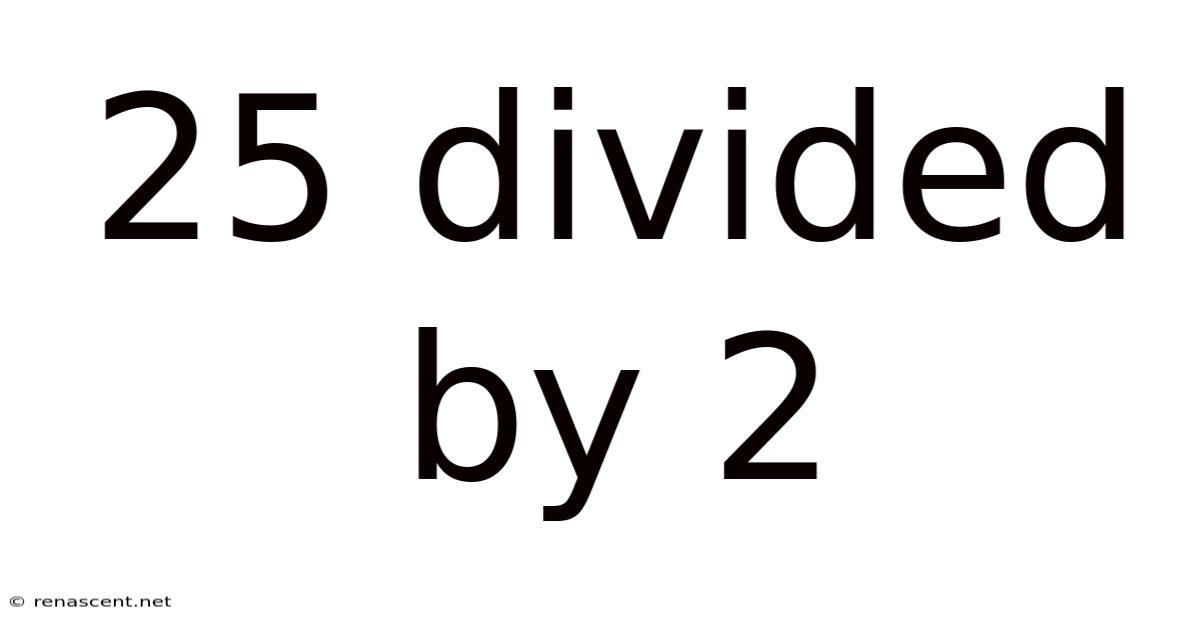
Table of Contents
25 Divided by 2: A Deep Dive into Division and its Applications
Understanding division is fundamental to mathematics and has far-reaching applications in various fields. This article explores the seemingly simple calculation of 25 divided by 2, delving into the different ways to approach the problem, the underlying mathematical principles, and real-world examples demonstrating its practical relevance. We'll uncover why understanding this seemingly basic concept is crucial for grasping more advanced mathematical concepts and problem-solving.
Introduction: Beyond the Basic Calculation
At first glance, 25 divided by 2 seems straightforward. A quick calculation might lead you to the answer: 12.5 or 12 with a remainder of 1. However, this seemingly simple operation opens a door to a wealth of mathematical concepts, including integers, decimals, fractions, and remainders. Understanding these concepts is not just about getting the right answer; it’s about developing a robust understanding of the very foundation of arithmetic. This article aims to provide a comprehensive understanding of 25 divided by 2 and its implications.
Method 1: Long Division
The traditional method of tackling 25 divided by 2 is through long division. This method provides a step-by-step approach that helps visualize the process and understand the concept of remainders.
-
Set up the problem: Write 25 inside the long division symbol (÷) and 2 outside.
-
Divide the tens: How many times does 2 go into 2 (the tens digit of 25)? The answer is 1. Write 1 above the 2 in 25.
-
Multiply and subtract: Multiply the quotient (1) by the divisor (2), which equals 2. Subtract this from the tens digit of the dividend (25), resulting in 0.
-
Bring down the ones: Bring down the ones digit of the dividend (5).
-
Divide the ones: How many times does 2 go into 5? The answer is 2 with a remainder. Write 2 above the 5.
-
Multiply and subtract: Multiply the quotient (2) by the divisor (2), which is 4. Subtract this from 5, leaving a remainder of 1.
Therefore, using long division, 25 divided by 2 is 12 with a remainder of 1. This can be written as 12 R 1.
Method 2: Using Decimals
Instead of a remainder, we can express the result as a decimal. To do this, we continue the long division process.
-
Add a decimal point: After obtaining the remainder of 1, add a decimal point to the dividend (25) and add a zero. This doesn't change the value, but allows us to continue dividing.
-
Divide the remainder: Now we have 10. How many times does 2 go into 10? The answer is 5.
-
Multiply and subtract: 5 multiplied by 2 is 10. Subtracting 10 from 10 leaves a remainder of 0.
Therefore, 25 divided by 2 is 12.5.
Method 3: Fractions
Another way to represent 25 divided by 2 is using fractions. Division can be expressed as a fraction, where the dividend (25) is the numerator and the divisor (2) is the denominator.
25 ÷ 2 = 25/2
This fraction can be simplified or expressed as a mixed number. 25 divided by 2 is 12 with a remainder of 1, so the mixed number representation is 12 1/2. This is equivalent to 12.5.
The Importance of Remainders and Decimals
The remainder in the long division method and the decimal in the decimal method both represent the portion of the dividend that wasn't completely divisible by the divisor. Understanding how to handle remainders is essential in many real-world scenarios. For instance, if you're dividing 25 cookies equally among 2 friends, each friend gets 12 cookies, and you have 1 cookie left over. The decimal representation, 12.5, might be more relevant if you're dealing with continuous quantities like weight or volume. Each friend would receive 12.5 units.
Real-World Applications: Where 25 Divided by 2 Matters
The seemingly simple calculation of 25 divided by 2 has practical applications in numerous areas:
- Sharing Resources: Dividing resources equally among individuals, as in the cookie example.
- Calculating Averages: Finding the average of two numbers. For example, finding the average of 20 and 30 would involve (20 + 30) / 2 = 25. If you then need to divide that average by 2, the result is 12.5.
- Measurement and Conversion: Converting units of measurement. For example, converting 25 inches into feet (12 inches per foot).
- Financial Calculations: Dividing costs or profits equally among partners.
- Data Analysis: Dividing data sets into smaller groups for easier analysis.
- Programming and Computing: In computer programming, division is a fundamental operation used in numerous algorithms and calculations.
- Engineering and Physics: Many engineering and physics problems involve dividing quantities to determine ratios, proportions, and other essential parameters.
Understanding the Underlying Mathematical Principles
The calculation of 25 divided by 2 hinges on several core mathematical concepts:
- Dividend: The number being divided (25 in this case).
- Divisor: The number by which the dividend is divided (2 in this case).
- Quotient: The result of the division (12 or 12.5).
- Remainder: The amount left over after division (1 in this case).
- Integers: Whole numbers (positive, negative, or zero).
- Decimals: Numbers containing a decimal point, representing parts of a whole.
- Fractions: Numbers representing parts of a whole, expressed as a ratio of two integers.
Advanced Concepts: Connecting to Higher Mathematics
The concept of division, as illustrated by 25 divided by 2, lays the groundwork for more advanced mathematical concepts:
- Algebra: Division is crucial in solving algebraic equations.
- Calculus: Division is used extensively in differentiation and integration.
- Statistics: Division is used in calculating averages, standard deviations, and other statistical measures.
- Linear Algebra: Matrices and vectors often involve division operations.
Frequently Asked Questions (FAQs)
-
What is the difference between a remainder and a decimal? A remainder represents the leftover whole number after division, while a decimal represents the fractional part of the result.
-
Can I always express a division result as a decimal? Yes, any division result can be expressed as a decimal, though some decimals may be infinitely long (repeating decimals).
-
Why is understanding division important? Division is a fundamental operation in mathematics, essential for problem-solving in many real-world contexts and for understanding more advanced mathematical concepts.
-
Are there other ways to represent 25 divided by 2? Yes, besides decimals and remainders, you can represent it as a fraction (25/2) or a mixed number (12 1/2).
Conclusion: The Significance of a Simple Calculation
The seemingly simple calculation of 25 divided by 2 provides a window into the profound world of mathematics. By exploring different methods, understanding remainders and decimals, and recognizing its diverse applications, we gain a much deeper appreciation for this fundamental operation. This seemingly simple division problem illuminates the building blocks of arithmetic, laying a strong foundation for more complex mathematical concepts and problem-solving skills in various fields. The ability to confidently approach and solve this type of problem is an essential stepping stone to success in mathematics and beyond. It's a testament to the power of understanding fundamental mathematical principles and their vast applications in the real world.
Latest Posts
Latest Posts
-
150 Gm To Oz
Sep 21, 2025
-
1 7 Kgs In Pounds
Sep 21, 2025
-
Ammo Can 50 Cal
Sep 21, 2025
-
18 Divided By 30
Sep 21, 2025
-
Acetic Acid Sodium Hydroxide
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 25 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.